初中数学中考几何最值问题

这是一份初中数学中考几何最值问题，共14页。PPT课件主要包含了从以下几个方面，两个定点的问题，在圆柱体中的运用，在正方形中的运用，在梯形中的运用，在圆中的运用，在坐标系中的运用，在一次函数中的运用，在菱形中的运用，在角中的运用等内容，欢迎下载使用。

最值问题是初中数学的重要内容，无论是代数问题还是几何问题都有最值问题，在中考中出现频率比较高。主要利用几何的重要结论（如两点之间线段最短，垂线段最短，三角形两边之和大于第三边，三角形两边之差小于第三边等）以及用一次函数和二次函数性质来求最值问题。
两个定点的问题就是把问题转化成两点之间的线段，利用两点之间线段最短来解决。
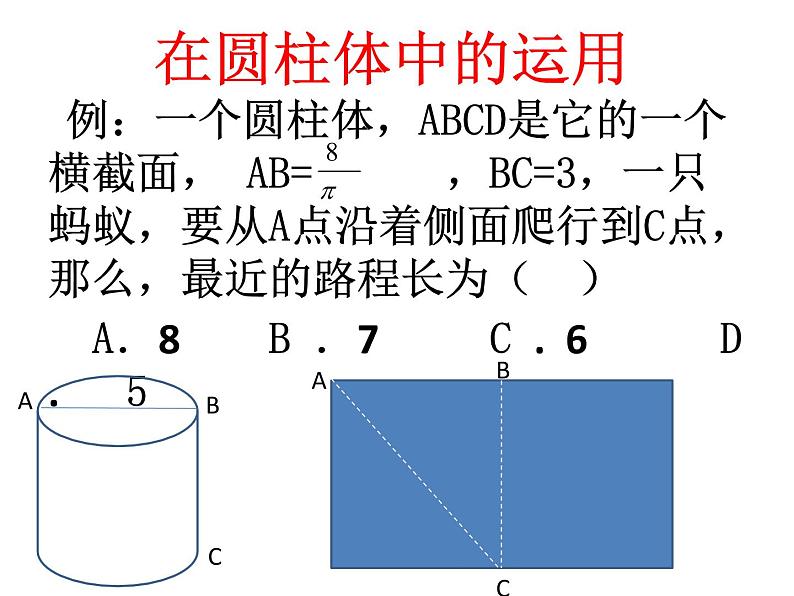
在圆柱体中的运用
例：一个圆柱体，ABCD是它的一个横截面， AB= ，BC=3，一只 蚂蚁，要从A点沿着侧面爬行到C点，那么，最近的路程长为（  ）    A．8  B ．7   C . 6  D . 5
在长方体中的运用
有一长、宽、高分别是5cm，4cm，3cm的长方体木块，一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上和A相对的顶点B处，则需要爬行的最短路径长为（  ） A  B C   D
二、从对称的角度研究最值问题
1、两个定点与一条直线上一个动点的问题
模型一:如图，A、B两点在直线l两侧，请在l上找一点P1，使AP1+BP1最小；在l上找一点P2，使AP2－BP2最大。
模型二:如图，A、B两点在直线l同侧，请在l上找一点P1，使AP1+BP1最小；在l上找一点P2，使AP2－BP2最大。
（2017泰安）如图 所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使 PD+PE的和最小，则这个最小值为（     ）   A．2   B．2      C．3    D．
已知直角梯形ABCD中，AD∥BC,AB⊥BC，AD=2,BC=DC=5,点P在BC上移动，则当PA+PD取最小值时，APD中边AP上的高为（   ）  A      B   C    D．3
如图，AB、CD是半径为5的⊙O的两条弦，AB = 8，CD = 6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为:( )
在平面直角坐标系中，有点A（3，－2），点B（4，2）两点，现另取一点C（1，n），当n = （      ）时，AC + BC的值最小．
已知：点A（1,2）、点B(3,6),在X轴上找一点P(x,0)(1)当x为何值时，PA+PB值最小(2)当x为何值时，PB- PA值最大
一次函数y=kx＋b的图象与x、y轴分别交于点A(2，0)，B(0，4)．(1)求该函数的解析式； (2)O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点的坐标．
2、一个定点和两条直线上两个动点的问题 问题：在∠AOB内有一定点P,在OA边上求点C,在OB边上求点D,使PC+CD值最小。
（2018贵港）已知:菱形ABCD的边长为4 , B=600 . E为BC上的一动点，F为AB上的一动点，P为AC上一个定点，则PE+PF的最小值为 （ ）  
已知： AOB=450，点P是 AOB内一点，PO= 10，Q、R分别是OA和OB上的动点，求： PQR周长的最小值
变式：如图，在四边形ABCD中，∠BAD=1200,∠B= ∠D=900,在BC,CD上分别找一点M,N使△AMN周长最小，求∠ANM+∠AMN的度数。
3、两个定点和两条直线上两个动点的问题 问题：在∠AOB内有两个定点P、Q,在OA边上求点C,在OB边上求点D,使四边形PQDC周长最小。
（2016武汉）在矩形ABCD中，E是AB边的中点，F在AD边上，M,N分别是CD、BC边上的动点，若AB=AF=2,AD=3,则四边形EFMN周长的最小值是（ ）
变式：如图已知正方形ABCD边长为3，点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时， 求：四边形AEPQ的面积。
三、从平移的角度研究最值问题
例：在河的两岸有张庄和李庄，张庄距河边100米，李庄距河边200米，张庄在李庄的东北方向，河的宽度100米，现在要在河上建一座桥（桥与两岸垂直），问桥建在什么地方使张庄到李庄的路程最小，最小路程为多少？ 
利用对称点、平移研究最值
已知：点M(2,3) ,点N(4,5) ,线段AB在X轴上，线段AB的长为2，当点B坐标为多少时，四边形MNBA的周长 最小。
已知：等腰直角三角形ABC和等腰直角三角形EFH的直角边长分别为2 和 ，斜边BC、FH都在X轴上 ， EFH在X轴上平移， ABC位置不动，设H点的坐标为（x,0），连接AE、AF,当 AEF周长最小时，求：x值
四、从旋转的角度研究最值问题
从旋转角度研究最值主要在圆内考查1、利用过圆内一点的所有弦中，直径最长，垂直于直径的弦最短2、“隐圆”中的最值问题
如图，AB是圆O的一条弦，点C是圆O上一动点，且∠ACB=300 ,点E,F分别是AC,BC的中点，直线EF与圆O交于G,H两点。若圆O半径为5，则GE+FH的最大值为 ( ).
已知：正方形ABCD的边长为1，E为边AD上一动点（不含A)，将 ABE沿BE折叠，点A落在点P处，求：PD的最小值。
（2020徐州）在△ABC中，若AB=6,∠ACB=45°，则△ABC的面积的最大值为 （ ）。
五、从代数几何综合运用的角度研究最值问题
已知：在三角形ABC中，AB=AC=5, BC=6,E为边AB上一动点（不同于A ,B），过E作EF//BC交AC于点F，分别过E、F作BC的垂线于点G ,H，求矩形EFGH的面积最大值。
（2018大庆）抛物线y=x2-5x+4与x轴相交于A,B两点，点B坐标为（4,0），与y轴交于点C(0,4),点P在x轴下方的抛物线上，过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值。
（2020扬州）如图在平行四边形ABCD中，∠B=60°，AB=10,BC=8,点E为边AB上的动点，连接ED并延长至点F,使得DF=1/4DE,以EC,EF为邻边构造平行四边形EFGC,连接EG,求 EG的最小值