初中数学人教版八年级上册14.3.2 公式法优质课ppt课件

这是一份初中数学人教版八年级上册14.3.2 公式法优质课ppt课件，共21页。PPT课件主要包含了因式分解，整式乘法，11a2，7a22，把下列各式分解因式，m²-32，3解a4-b4，x3y-9xy3，提取公因式，x4x2-1等内容，欢迎下载使用。

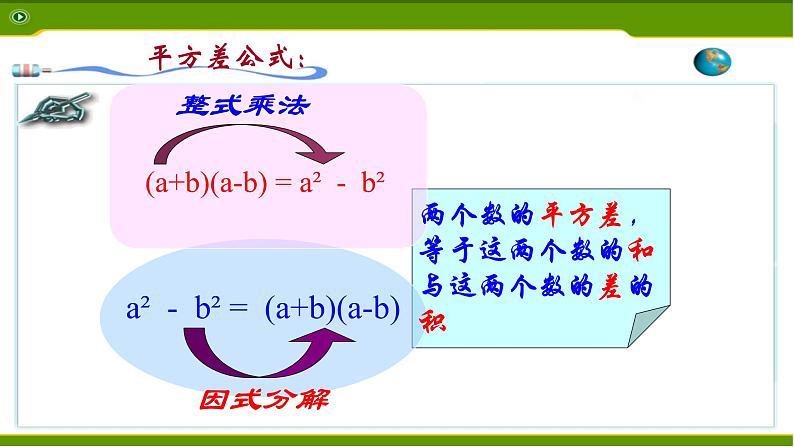
a² - b² = (a+b)(a-b)
平方差公式：(a+b)(a-b) = a² - b²
两个数的平方差，等于这两个数的和与这两个数的差的积
1.把下列各式写成完全平方的形式： 如：36x2y4=( 6xy2) 2
(0.2a3 b ) 2
[0.4(a-b)] 2
平方差公式:a2-b2 =(a+b)(a-b)
(2) m² - 9
(3) x² - 4y²
=（x+1) (x-1)
=（m+3)(m-3)
=（x+2y) (x-2y)
(1) x² - 1
=x² - 12
=x² - (2y)2
a2 − b2
= (a + b) (a-b)
思考：什么样的多项式才可以用平方差公式分解因式？
1.具备什么特征的多项式是平方差式?
答：一个多项式如果是由两项组成，两部分是两个式子(或数)的平方，并且这两项的符号为异号.
2.运用a2-b2=(a+b)(a-b)公式时,如何区分a、b?
答:平方前符号为正，平方下的式子（数）为ａ 平方前符号为负，平方下的式子（数）为ｂ
感受新知----算一算
下列多项式可以用平方差公式分解因式吗？
① 4x2+y2 ②－0.49x2+ y2 ③ －4x2－y2 ④ 9+(－y)2
公式中a、b可以是单独的数或字母，也可以是单项式或多项式。
如果一个多项式可以转化为a2-b2的形式，那么这个多项式就可以用平方差公式分解因式。
(1)16a²- 1 (2) -m²n²+4x²(3) — x² - — y4
4.( x + z )²- ( y + z )²
1.解:原式= (4a)²-1²= (4a+1)(4a-1)
2.解:原式=4x2-m ²n ² =(2x) ²-(mn) ²
例1.把下列各式分解因式
=(2x+mn)(2x-mn)
=[(x+z)+(y+z) ][(x+z)-(y+z)]
=(x+y+2z)(x-y)
=(5x+2)5x-2)
=(11)2-(2ab)2
=(11+2ab)(11-2ab)
=(2x)2-( )2
运用新知----算一算
=(2m+2n+m-n)(2m+2n-m+n)
=(3m+n)(m+3n)
深入探索----算一算
通过做第(2)小题你总结出什么经验来了吗?
分解因式时,通常先考虑是否能提公因式,然后再考虑能否进一步分解因式.
=(a2-b2)(a2+b2)
=(a+b)(a-b)(a2+b2)
通过做第(3)小题你总结出什么吗?
分解因式一直到不能分解为止.所以分解后一定检查括号内是否能继续分解.
（4）9(m+n)2-(m-n)2
9(m+n)2-(m-n)2
＝[3(m+n)]2-(m-n)2
＝[3(m+n)+(m-n)][3(m+n)-(m-n)]
＝(3m+3n+m-n) (3m+3n-m+n)
＝(4m+2n) (2m+4n)
＝4 (2m+n) (m+2n)
=xy(4x2-9y2)
2.应用平方差公式分解
3.分解到每个因式不能再分解为止
对于分解复杂的多项式，我们应该怎么做？
总结反思----算一算
1．证明：两个连续偶数的平方差能被4整除吗？请与你的同伴交流。
2．248－1可以被60和70之间的两个数整除，请求出这两个数。
拓展提高----算一算
知识抢答----玩中学
(1) 4x3 -x
=x(2x+1)(2x-1)
(2) 4a² - 16b²
=4 (a²- 4b²)
= 4 (a+ 2b) (a- 2b)
= (a2+9)(a2-9)
= (a2+9)(a+3) (a-3)
计算（1）20052 - 20042
解: 20052-20042
（2） 25×2652－1352×25
=(2005+2004)(2005-2004)
=25×(265+135)(265－135)
解: 原式=25×(2652－1352)
=25×400×130
计算: 4( a + b )²- 25( a -c )²
=(7a+2b-5c)(2b -3a+5c)
=[2(a+b)]²-[5(a-c)]²
=[2(a+b)+ 5(a-c)][2(a+b) - 5(a-c)]
解：4( a + b )²- 25( a -c )²