人教版八年级上册本节综合精品ppt课件

这是一份人教版八年级上册本节综合精品ppt课件，共47页。PPT课件主要包含了§1131多边形，观察下列图案，生活中的平面图形，了解一下，想一想，猜想与说理，强化训练等内容，欢迎下载使用。
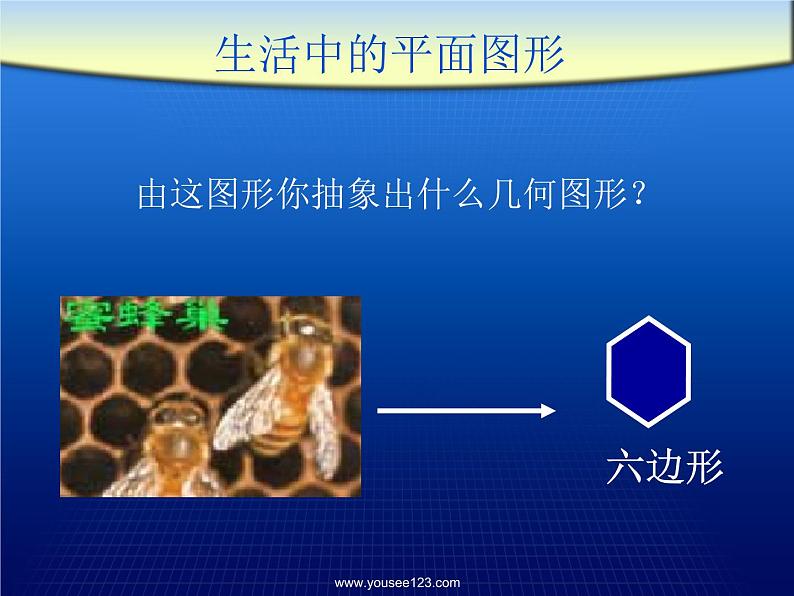
由这图形你抽象出什么几何图形？
在平面内，由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
你能仿照三角形的定义给出多边形的定义吗？
对角线：连接多边形不相邻的两个顶点的线段。
可表示为：五边形ABCDE或五边形DCBAE
内角：多边形相邻两边组成的角
外角：多边形的边与它的邻边 的延长线组成的角。
你能说出这两幅图形的异同点吗？
如图（1）这样，画出多边形的任何一条边所在的直线，整个四边形都在这条直线的同一侧，那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
观察下面多边形，它们的边，角有什么特点？
在平面内，内角都相等，边也都相等的多边形叫做正多边形
11.3.2 多边形的内角和
1、在平面内，_____________________叫做多边形。２、在多边形中连接_________________的线段叫做多边形的对角线。３、三角形的内角和是_____度．４、你能够利用三角形的内角和求四边形的内角和吗？试试看？
思路：多边形问题转化为三角形问题来解决．
四边形的内角和为360０
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点的线段
长方形的内角和是多少？为什么？
（1）四边形ABCD的内角 和是多少？（2）你是怎样求的？
(1)从顶点A可以画几条对角线？分别是哪几条？
(2)这样五边形被分成了几个三角形？
(3)五边形的内角和是多少度？
你来探索六边形的内角和，你一定行！
这种探索方法你掌握了吗？请完成下表
想一想：从表中你能发现什么？
n边形的内角和等于(n－2)．180°
An A5
A1 A4
A2 A3
A2 A3
你还有其他的方法将多边形分割成三角形吗？
该图中n边形共有n个三角形，故所有三角形内角和为n×180 °，但每个图中都有一个以红圈圈住的点，它是一个圆周角360 °，因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
这种分割方式，将多边形分成n-1个三角形，故所有三角形的内角和为（n-1）×180 °，边上一点周围所形成的平角不是多边形的内角，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 °
例1：求八边形的内角和的度数。
解：（n－2）×180°＝（8－2）×180° ＝1080°答：八边形的内角和为1080°。
例2：一个正多边形的一个内角为150°， 你知道它是几边形吗？
解：设　这个多边形为n边形，根据题意得：　　　　（n－2）×180＝1５0n　　 　　 　 n＝12答：这个多边形是12边形。
另解：由于多边形外角和等于360° 而这个正多边形的每个外角都等于 180°－150°＝30°， 所以这个正 多边形的边数等于 360°÷30°＝12。
例题3、已知两个多边形的内角和为1440°，且两多边形的边数之比为1︰3，求它们的边数分别是多少？
牛刀小试： （1）八边形的内角和等于 。 （2）已知一个多边形的内角和等于2340°， 它的边数是 。 （3）小明在计算多边形的内角和时求得的 度数是1000°，他的答案正确吗？为 什么？
（4）已知四边形4个内角的度数比是1︰2︰3︰4， 那么这个四边形中最大角的度数是 。（5）一个五边形的三个内角是直角，另两个内角 都是n°，则n= 。（6）六角螺母的面是六边形，它的内角都相等，则 这个六边形的每个内角是 　　　　 。 （7）在四边形ABCD中，∠A与∠C互补，那么∠B 与∠D有什么关系呢？为什么？
（1）什么是三角形的外角？外角有什么性质？
（2）类似地，在多边形中找出外角
多边形的一边与另一边的延长线的夹角，叫做多边形的外角。
（1）如图，求△ABC的三个外角的和。
三角形的三个外角之和为3600
（2）四边形的外角和等于多少度？
（3）五边形的外角和怎么求？n边形呢？
n边形的外角和是多少度呢?
答:都是360°.因为多边形的外角与它相邻的内角是邻补角，所以n边形的外角和加内角和等于n·180°，内角和为(n－2)·180°,因此，外角和为：n·180°－(n－2)·180°= 360°.
结论:多边形的外角和都等于360°.
例1：一个多边形的内角和等 于它的外角和的3倍，它 是几边形？
解：设它是n边形，则(n-2).180=3×360解得：n=8答：它是8边形
例2：一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解：设一个外角为x°， 则内角为（x＋36）° 根据题意得：　　 x+x+36＝180　　 　 x＝72 360÷72＝5答：这个正多边形为正五边形。
三角形三个内角的度数分别是（x+y), (x-y),x,且x>y>0,则该三角形有一个内角为 （　　）A、30OB、45OC、60OD、90O2.一个正多边形每一个内角都是120，这个多边形是（　　）A、正四边形B、正五边形　　C、正六边形D、正七边形
３．一个多边形木板，截去一个三角形后（截线不经过顶点），得到新多边形内角和为2160，则原多边形的边数为（　）A、13条B、14条C、15条D、16条下列说法中，错误的是（　　）　　A、一个三角形中至少有一个角不大于60O；　　B、有一个外角是锐角的三角形是钝角三角形；C、三角形的外角中必有两个角是钝角；　　　D、锐角三角形中两锐角的和必然小于60O；
5.小明绕五边形各边走一圈，他共转了_ __度。6.下列正多边形（1）正三角形（2）正方形（3）正五边形（4）正六边形，其中用一种正多边形能镶嵌成平面图案的是　　　　　；
（1）、（2）、（4）
7.如下图，AD是BC边上的高，BE是 △ ABD的角平分线，∠1=40°，∠2=30°，则∠C=_ __∠BED= 。
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
思考、有一六边形，截去一三角形，内角和会发生怎样变化？请画图说明。
如图， ∠Ａ＝４５°， ∠Ｂ＝２５ ° ∠Ｃ＝３０ ° ，则 ∠Ｄ＝　　　　　。
如图， ∠Ａ＋∠Ｂ＋∠Ｃ＋∠Ｅ＋∠Ｆ＝　　　　　。
巩固一下：1.求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G的度数。
7×180O－2×360O＝540O