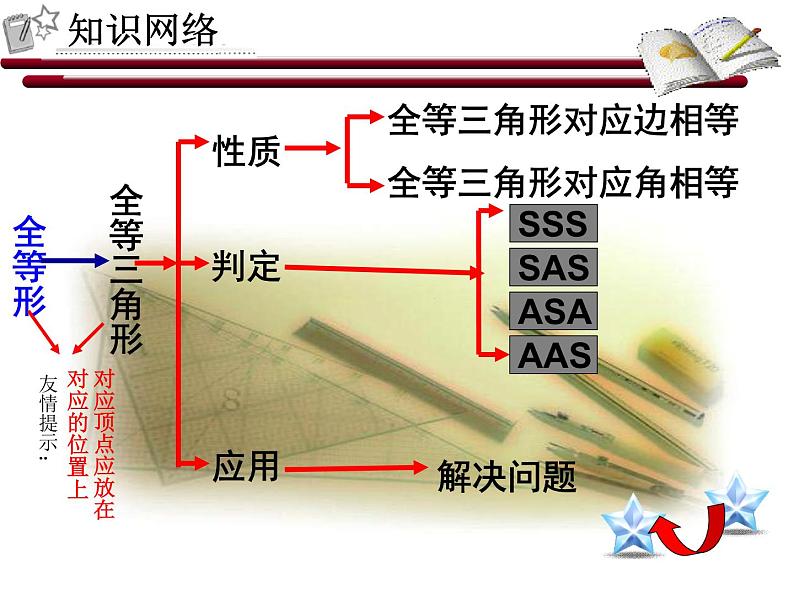
初中人教版12.1 全等三角形优质ppt课件

这是一份初中人教版12.1 全等三角形优质ppt课件，共17页。PPT课件主要包含了第八章全等三角形，全等形，全等三角形，全等三角形对应边相等，全等三角形对应角相等，解决问题，SSS，SAS，ASA，AAS等内容，欢迎下载使用。

熟练掌握全等三角形的4种判定方法。
能根据已知条件选择正确的判定方法说明两个三角形全等。
在全等三角形的说理过程中，重视学生逻辑思维的发展，重视文字语言、符号语言、图形语言的相互转译，并能正确书写推理过程。
活动1 熟悉三角形全等知识结构，掌握 全等判定的条件。活动2 复习全等三角形中的基本图形活动3 典型题解活动4 课堂小结活动5 作业布置
对应顶点应放在对应的位置上
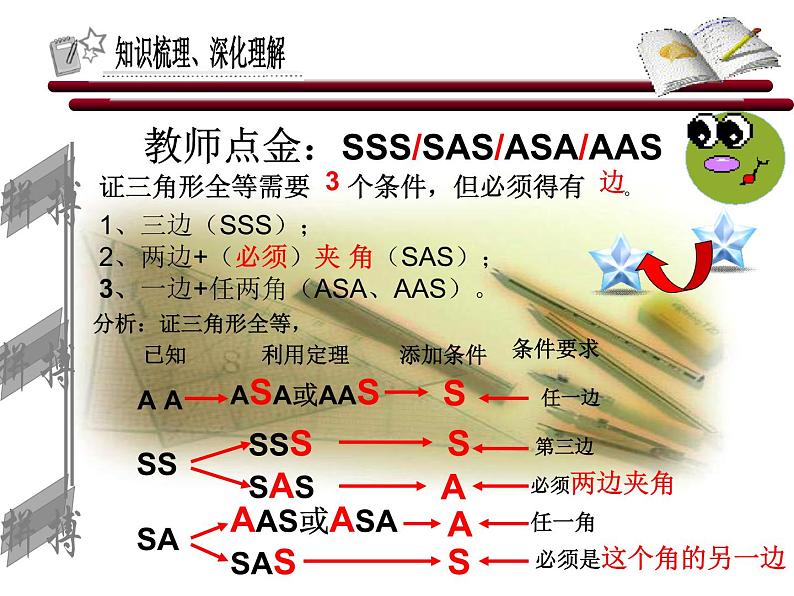
教师点金：SSS/SAS/ASA/AAS证三角形全等需要 个条件，但必须得有 。
1、三边（SSS）；2、两边+（必须）夹 角（SAS）；3、一边+任两角（ASA、AAS）。
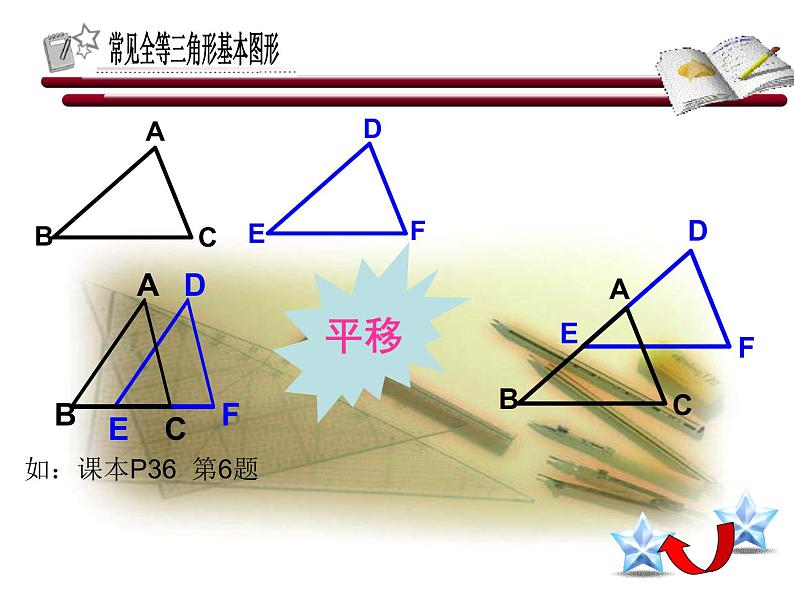
如：课本P36 第6题
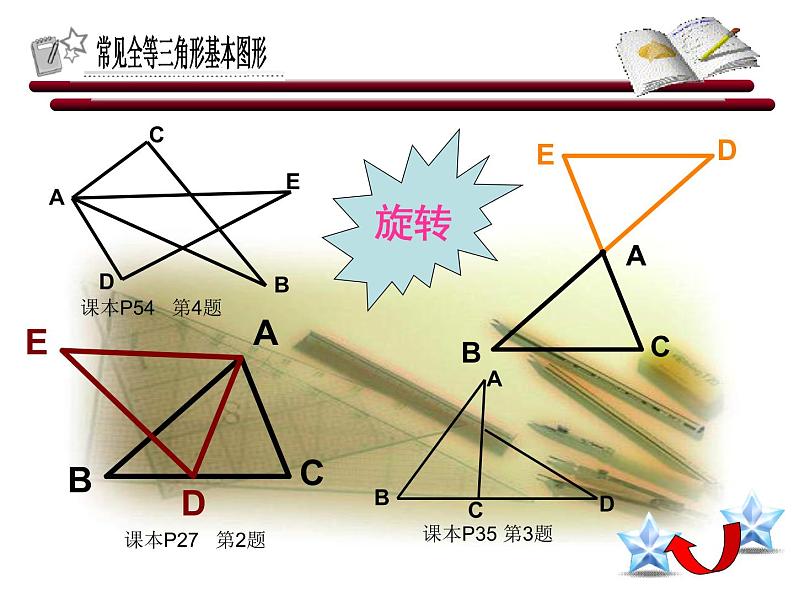
课本P27 第2题
课本P54 第4题
课本P54 第3题
课本P36 第1题
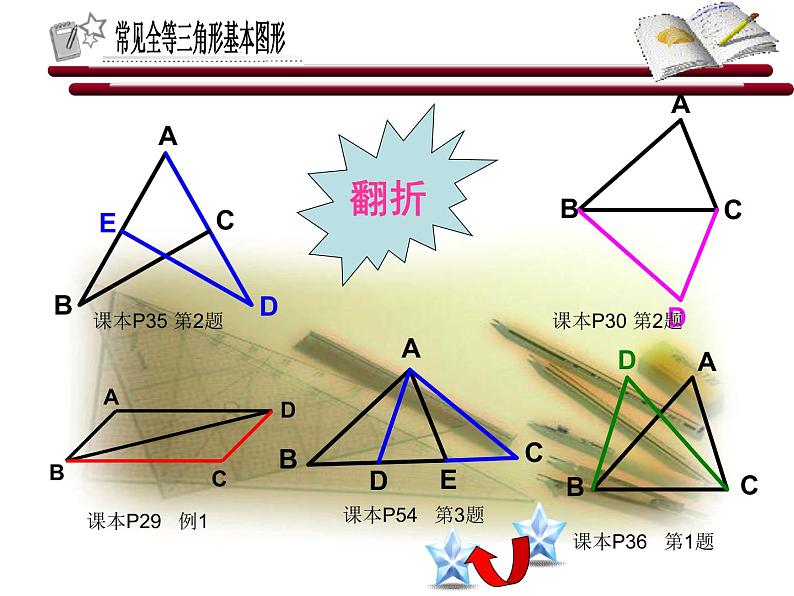
教师点评：在解决全等三角形问题时，从复杂的图形中分解出基本图形，解题就会变得简便。
互动P27 6题
互动P29 7题
例1 ：如图,点B在AE上∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
①用SAS,需要补充条件AD=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以?
S→ AB=AB(公共边) .
分析：现在我们已知 A→∠CAB=∠DAB
SSS/SAS/ASA/AAS
2.已知：如图，AB=AC, ∠1=∠3, 请你再添一个条件，使得∠E=∠D？为什么？
1.已知：如图，AB=AC,AD=AE, 请你再添一个条件，使得∠E=∠D？为什么？
教师点评： 这道例题的选择是想通过变式，加深了我们对判定方法的灵活应用。
如图,A是CD上的一点,⊿ABC ,⊿ADE 都是正三角形,求证CE=BD
分析:证⊿ABD≌⊿ACE
变式:在原题条件不变的前提下,可以探求以下结论:(1)求证:⊿ABF≌⊿ACG;(2)求证:AG=AF;(3)连结GF,求证⊿AGF是正三角形;(4)求证GF//CD
如图,分别以⊿ABC的边AB,AC为一边画正方形AEDB和正方形ACFG,连结CE,BG.求证BG=CE
分析:此题是把两个三角形改成两个正方形而以,证法类同
点评：设置一系列有梯度的变式练习，使同学们通过系统的演练，对《全等三角形》知识达到熟练的程度。现在的标准化考试的特点是考查综合运用知识的能力。因此复习时，除了要掌握必备的基础知识外还要具备综合运用知识的能力，防止出现思维误区。
教师定评： 1.证明两个三角形全等，要结合题目的条件和结论，选择恰当的判定方法 2.全等三角形，是证明两条线段或两个角相等的重要方法之一，证明时 ①要观察待证的线段或角，在哪两个可能全等的三角形中。 ②分析要证两个三角形全等，已有什么条件，还缺什么条件。 ③想着公共边和对顶角等隐含条件 3.注意正确地书写证明格式(注意顺序和对应关系).