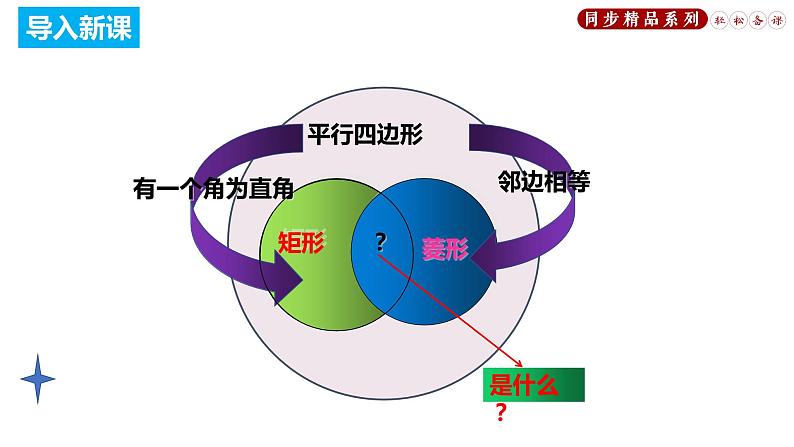
初中数学人教版八年级下册18.2.3 正方形教案配套课件ppt

这是一份初中数学人教版八年级下册18.2.3 正方形教案配套课件ppt，共29页。PPT课件主要包含了教学目标，重点难点，平行四边形，有一个角为直角，邻边相等，是什么，导入新课，正方形是特殊的矩形，邻边相等的矩形，正方形等内容，欢迎下载使用。

1.知识与技能 掌握正方形的概念、性质和判定，并会用它们进行有关的论证和计算。 2.过程与方法 进一步发展合情推理、演绎推理的能力，增强几何直观和几何符号意识。 3.情感态度和价值观 通过正方形与平行四边形、矩形、菱形的联系的教学对学生进行辩证唯物主义教育，提高学生的逻辑思维能力。
重点：正方形的定义及正方形与平行四边形、矩形、菱形的联系。 难点：正方形与矩形、菱形的关系及正方形性质与判定的灵活运用。
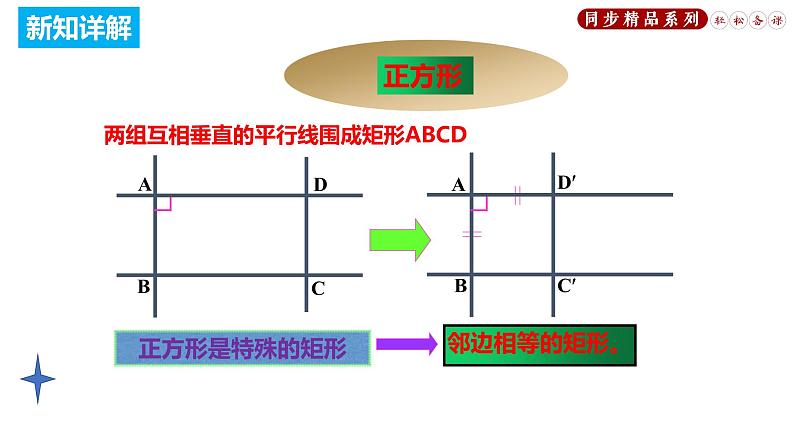
两组互相垂直的平行线围成矩形ABCD
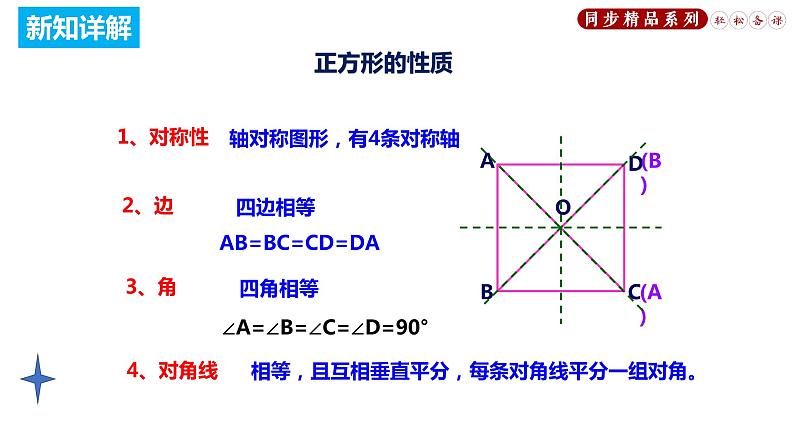
轴对称图形，有4条对称轴
AB=BC=CD=DA
∠A=∠B=∠C=∠D=90°
相等，且互相垂直平分，每条对角线平分一组对角。
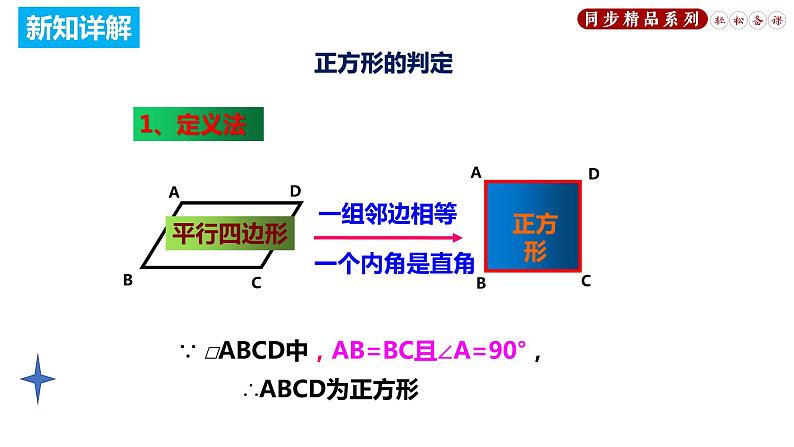
∵ □ABCD中，AB=BC且∠A=90°，
∵ 菱形ABCD中，∠A=90°，
∵ 矩形ABCD中，AB=BC，
∴ABCD为正方形.
已知：如图四边形ABCD是正方形，对角线AC、BD交于点O。求证： △ ABO、 △ BCO、 △ CDO、 △ DAO是全等的等腰直角三角形。
　　例5　求证：正方形的两条对角线把这个正方形分　　成四个全等的等腰直角三角形．
证明：∵四边形ABCD是正方形， ∠B=90° ∴AC=BD，AC ⊥ BD,AO=BO=CO=DO ∴△ ABO、 △ BCO、 △ CDO、 △ DAO是等腰直角三角形，且△ABO≌△BCO≌ △ CDO ≌ △ DAO
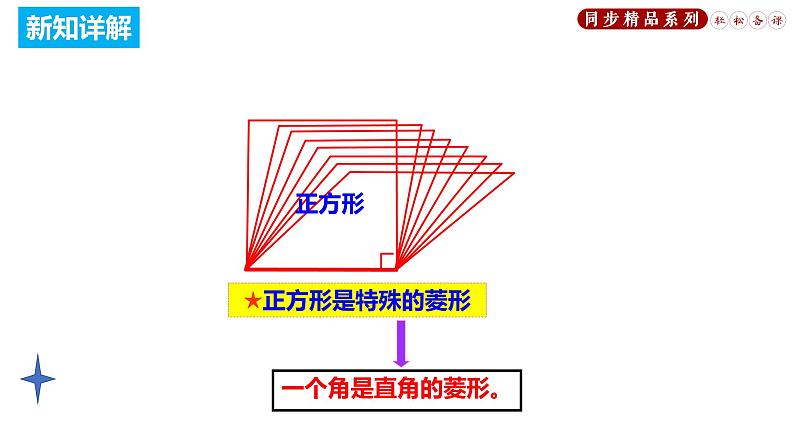
有一组邻边相等且有一个角是直角
1.在正方形ABCD的对角线AC上点E，使AE=AB，过E作EF⊥AC交BC于F，求证：（1）BF=EF；（2）BF=CE。
分析：连接AF，要求BF=EF，求证△AEF≌△ABF，可以求证EF=BF（2）根据（1）的结论，要求BF=CE，求证△CEF为等腰直角三角形即可
解析：（1）连接AF在Rt△AEF和Rt△ABF中，∵AF=AF，AE=AB，∴Rt△AEF≌Rt△ABF，∴BF=EF；
2.证明：（1）有一个角是直角的菱形是正方形；（2）对角线垂直的矩形是正方形。
分析：（1）由菱形的性质和已知条件得出AB=CD=BC=DA，四边形ABCD是矩形，得出∠A=∠B=∠C=∠D=90°，即可得出结论；（2）由矩形的性质和已知条件得出∠BAD=∠ABC=∠BCD=∠CDA=90°，四边形ABCD是菱形，得出AB=BC=CD=DA，即可得出结论．
解：（1）如图1所示：已知：四边形ABCD是菱形，∠A=90°；求证：四边形ABCD是正方形；证明：∵四边形ABCD是菱形，∠A=90°，∴AB=CD=BC=DA，四边形ABCD是矩形，∴∠A=∠B=∠C=∠D=90°，∴四边形ABCD是正方形；
解：（2）如图2所示：已知：四边形ABCD是矩形，对角线AC⊥BD；求证：四边形ABCD是正方形；证明：∵四边形ABCD是矩形，对角线AC⊥BD，∴∠BAD=∠ABC=∠BCD=∠CDA=90°，四边形ABCD是菱形，∴AB=BC=CD=DA，∴四边形ABCD是正方形．
3.已知△ABC，DE∥AC交AB于E，DF∥AB交AC于F．（1）四边形AEDF是什么四边形？（2）当△ABC满足什么条件时，四边形AEDF是矩形？（3）当线段AD满足什么条件时，四边形AEDF是菱形？（4）当△ABC满足什么条件时，四边形AEDF是正方形？
解：（1）∵DE∥AC，DF∥AB∴四边形AEDF是平行四边形；（2）∵一个角为直角的平行四边形为矩形，∴∠BAC=90°时，四边形AEDF是矩形；（3）∵菱形对角线互相垂直，∴当AD⊥EF时，四边形AEDF是菱形；（4）∵正方形既是菱形又是矩形，∴∠BAC=90°且AD⊥BC时，四边形AEDF是正方形．
1.如图，有一平行四边形ABCD与一正方形CEFG，其中E点在AD上．若∠ECD=35°，∠AEF=15°，则∠B的度数为何？（　　）A．50 B．55 C．70 D．75
分析：由平角的定义求出∠CED的度数，由三角形内角和定理求出∠D的度数，再由平行四边形的对角相等即可得出结果．
分析：阴影部分的面积=S△ACD-S△MEC，△ACD和△MEC都是等腰直角三角形，利用面积公式即可求解．
3.如图，四边形ABCD是正方形，以CD为边作等边三角形CDE，BE与AC相交于点M，则∠AMD的度数是（　　）A．75°B．60°C．54°D．67.5°
分析：连接BD，根据BD，AC为正方形的两条对角线可知AC为BD的垂直平分线，所以∠AMD=AMB，要求∠AMD，求∠AMB即可．
4.已知正方形ABCD，E为BC上任一点延长AB至F，使BF=BE，连AE并延长交CF于G，求证：AG⊥CF．
解析：如图，∵BE=BF，∴∠BFE=45°∵∠CAB=45°，∴FH⊥AC，又CB⊥AF，∴E是△ACF的垂心，因此AG⊥CF。
5.如图，在△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，DE⊥AB，DF⊥AC垂足分别为E，F．求证：四边形DEAF是正方形