数学人教版17.2 勾股定理的逆定理图文ppt课件

这是一份数学人教版17.2 勾股定理的逆定理图文ppt课件，共19页。PPT课件主要包含了导入新课，勾股定理的应用，应用四结论证明，新知详解，AB2-AC2，ABA’B’，ACA’C’，ABA＇B＇，ACA＇C＇，BCB＇C＇等内容，欢迎下载使用。

人教版八年级数学下册第十七章
17.1.3 勾股定理的应用2
你能在数轴上找到这两个点吗？
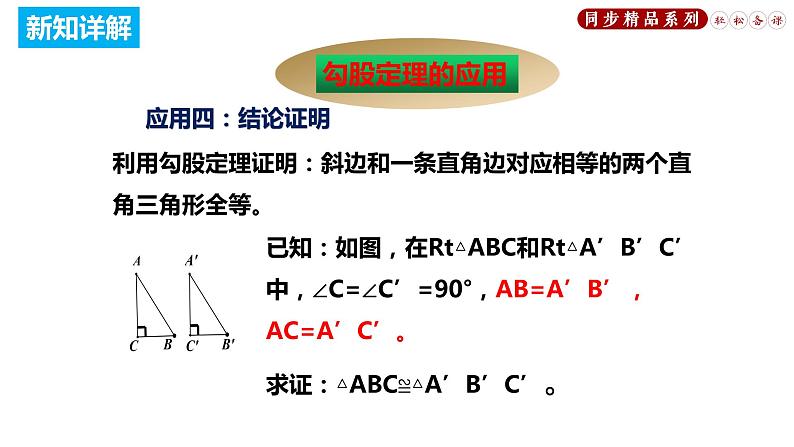
利用勾股定理证明：斜边和一条直角边对应相等的两个直角三角形全等。
已知：如图，在Rt△ABC和Rt△A’B’C’中，∠C=∠C’=90°，AB=A’B’，AC=A’C’。求证：△ABC≌△A’B’C’。
BC2=_ _______，B＇C＇2 =__ ___ __ ___.
证明：在Rt△ABC和Rt△A‘B’C‘中，∠C=∠C＇=90°，根据勾股定理，得
A’B’2-A’C’2
又∵_ _________， _____________.
在△ABC和△A＇B＇C＇中
∴___________≌__________（SSS）
1.如图，在Rt△ABC中，∠C=90°，D为AC上一点，且DA=DB=5，又△DAB的面积为10，那么DC的长是（　　）A．4B．3C．5D．4.5
分析：根据Rt△ABC中，∠C=90°，可证BC是△DAB的高，然后利用三角形面积公式求出BC的长，再利用勾股定理即可求出DC的长
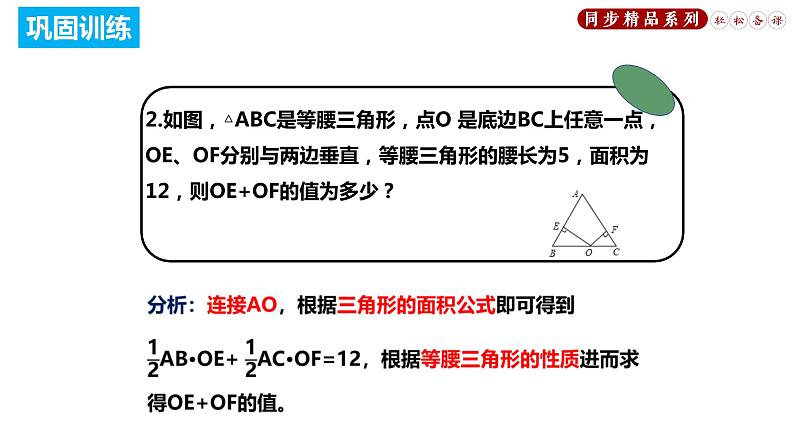
2.如图，△ABC是等腰三角形，点O 是底边BC上任意一点，OE、OF分别与两边垂直，等腰三角形的腰长为5，面积为12，则OE+OF的值为多少？
思考：两个直角边分别为2、3的直角三角形，其斜边长为 。
①在数轴上找到点A，使OA=3，
②过A点作直线L垂直于OA，在L上截取AB=2，
3.如图，A、B是4×5网格中的格点，网格中的每个小正方形的边长都是1，图中使以A、B、C为顶点的三角形是等腰三角形的格点C有（　　）A．2个B．3个C．4个D．5个
分析：先根据勾股定理求出AB的长，再根据等腰三角形的性质分别找出以AB为腰和以AB为底边的等腰三角形即可。
利用勾股定理的知识在数轴上表示无理数。
分析：首先作出AB、AD边上的点P（点A）到BD的垂线段AE，即点P到BD的最长距离，作出BC、CD的点P（点C）到BD的垂线段CF，即点P到BD的最长距离，由已知计算出AE、CF的长与3比较得出答案。