人教版八年级下册19.1.2 函数的图象背景图ppt课件

这是一份人教版八年级下册19.1.2 函数的图象背景图ppt课件，共27页。PPT课件主要包含了教学目标，重点难点，导入新课，函数的表示方法，新知详解，列表法，解析式法，图象法，yx+05，典例解析等内容，欢迎下载使用。
1.知道函数的三种表示法及其优缺点； 2.能用适当的方式表示简单实际问题中的变量之间的函数关系； 3.能对函数关系进行分析，对变量的变化情况进行初步讨论。
重点: 综合运用三种表示法表示函数关系，研究运动变化过程。 难点:正确选择表示方法。
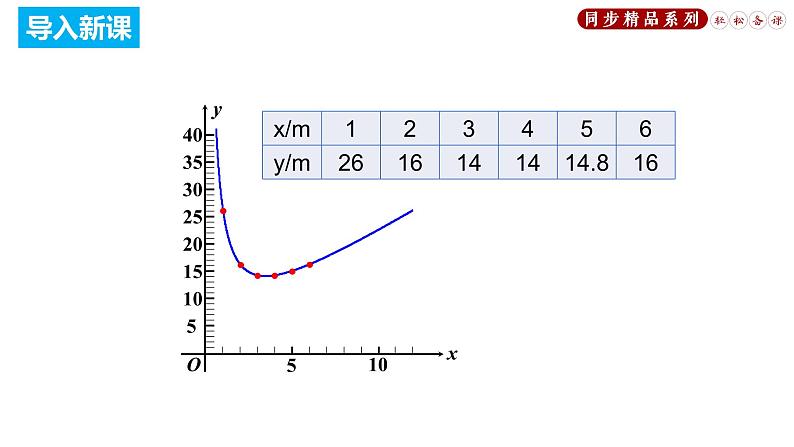
思考：如图，要做一个面积为12 m2的小花坛，该花坛的一边长为 x m，周长为 y m．　 （1）变量 y 是变量 x 的函数吗？　 （2）能求出这个问题的函数解析式吗？ （3）能画出函数的图象吗？
1、函数的表示方法有几种，分别是什么？
2、这三种表示函数的方法各有什么优点？
三种，分别是列表法、解析式法、图象法
列表法：具体地反映了函数与自变量的数值对应关系。
例如：表示某景区一周内的游客数量
解析式法：准确地反映了函数与自变量之间的数量关系。
如：正方形的面积S与边长a的关系：S=a2
物理中，物体的质量m与体积V的关系：m=ρV.
图象法：直观地反映了函数随自变量的变化而变化的规律。
如：右图为函数y=x+0.5的图象，从图象中，我们能够看到，函数y随x增大而增大。
例4：一水库的水位在最近5 h内持续上涨，下表记录了这5 h内6个时间点的水位高度，其中t表示时间，y表示水温高度.
(1)在平面直角坐标系中描出表中数据对应的点，这些点是否在一条直线上？由此你发现水位变化有什么规律吗？
描出表中6个点的位置，画图，得出这6个点在一条直线上。
猜想，在这5h内其他时刻，水位可能是始终以同一速度均匀上升的。
(2)水位高度y是否为时间t的函数? 如果是，试写出一个符合表中数据的函数解析式，并画出这个函数的图象.这个函数能表示水位变化的规律吗？
y=0.3t+3（0≤t ≤ 5）
表示经过th水位上升0.3tm
图象要注意t的取值范围
这个函数可以近似地表示水位的变化规律.
(3)据估计这种上涨规律还会持续2h，预测再过2h水位高度将为多少米？
由函数解析式：再过2h，即t=7h，则水位高度为：y=0.3×7+3=5.1m
由图象：将图象向右延伸到7所对应的位置，如图所示，同样可以得出结论。
函数的三种表示法通常是相互关联，可以相互转化(特殊的函数除外):
（1）由函数解析式可以得到这个函数的列表及图象。
（3）由函数的表格可以得到函数的解析式及图象。
（2）由函数的图象可以得到其解析式及函数的对应值表格。
列表法：一目了然，使用起来方便；但列出的对应值是有限的，不易看出自变量与函数之间的对应规律。
函数的表示方法优点和不足
解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系；但有些实际问题中的函数关系，不能用解析式表示。
图象法：形象直观；但只能近似地表达两个变量之间的函数关系。
1.弹簧挂上物体后会伸长，现测得一弹簧的长度y（厘米）与所挂物体的质量x（千克）之间有如下关系，下列说法不正确的是（　　）A．x与y都是变量，其中x是自变量，y是因变量B．弹簧不挂重物时的长度为0厘米C．在弹性范围内，所挂物体质量为7千克时，弹簧长度为13.5厘米D．在弹性范围内，所挂物体质量每增加1千克弹簧长度增加0.5厘米
2. “龟兔赛跑”讲述了这样的故事：领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点…用S1、S2分别表示乌龟和兔子所行的路程，t为时间，则图中与故事情节相吻合的是 ．（填序号）
解析：由题意可得，S1的始终是匀速增长，开始时，S2的增长比较快，但中间有一段时间S2停止增长．在最后一段时间里，S2的增长较快，但S2的值没有超过S1的值．结合所给的图象可知，应选（2），故答案为（2）．
1.如图所示，在边长为2的正方形ABCD的边上有一个动点P，从点A出发沿折线ABCD移动一周后，回到A点。设点A移动的路程为x，△PAC的面积为y，求函数y的解析式。
列表法、解析式法、图象法
1.某蓄水池的横断面示意图如图，分深水区和浅水区，如果这个注满水的蓄水池以固定的流量把水全部放出．下面的图象能大致表示水的深度h和放水时间t之间的关系的是（　　）A． B． C． D．
3.下表中的数据是根据某地区入学儿童人数编制的：（1）随着年份的变化，因变量入学儿童的人数变化的趋势是什么？答： ；（2）你认为入学儿童的人数会变成零吗？答： ．
4.心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间有如下关系（其中0≤x≤30）
（1）上表中反映了哪两个变量之间的关系？那个是自变量？哪个是因变量？（2）根据表格中的数据，你认为提出概念所用时间为几分钟时，学生的接受能力最强？（3）从表格中可知，当提出概念所用时间x在什么范围内，学生的接受能力逐步增强？当提出概念所用时间x在什么范围内，学生的接受能力逐步降低？（4）根据表格大致估计当提出概念所用时间为23分钟时，学生对概念的接受能力是多少？