初中数学人教版八年级下册18.2.1 矩形教课内容ppt课件

这是一份初中数学人教版八年级下册18.2.1 矩形教课内容ppt课件，共25页。PPT课件主要包含了试一试，矩形的性质，请证明这个命题，矩形对边平行且相等，它的对称轴有几条，AD4cm，平行四边形，有一个角是直角，练一练，拓展训练等内容，欢迎下载使用。

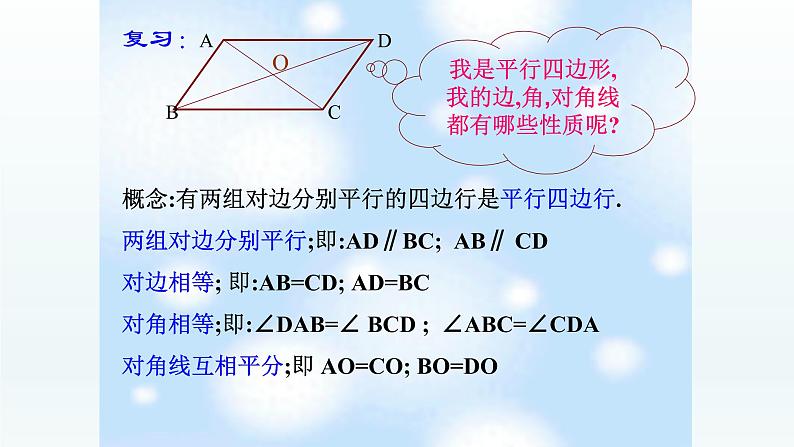
我是平行四边形,我的边,角,对角线都有哪些性质呢?
概念:有两组对边分别平行的四边行是平行四边行.两组对边分别平行;即:AD∥BC; AB∥ CD对边相等; 即:AB=CD; AD=BC对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA对角线互相平分;即 AO=CO; BO=DO
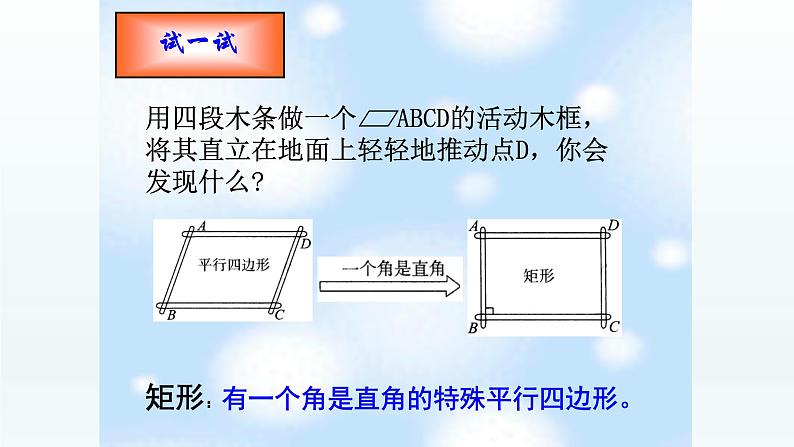
下图中有你认识的图形吗？
矩形：有一个角是直角的特殊平行四边形。
其实我还是平行四边形啊！只是我比较特殊而已，大家发现了我的特殊之处吗？
A D B C
1、画一个矩形ABCD。
2、从边、角、对角线三方面进行考虑，你能发现什么吗？矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？请以小组的形式讨论总结。
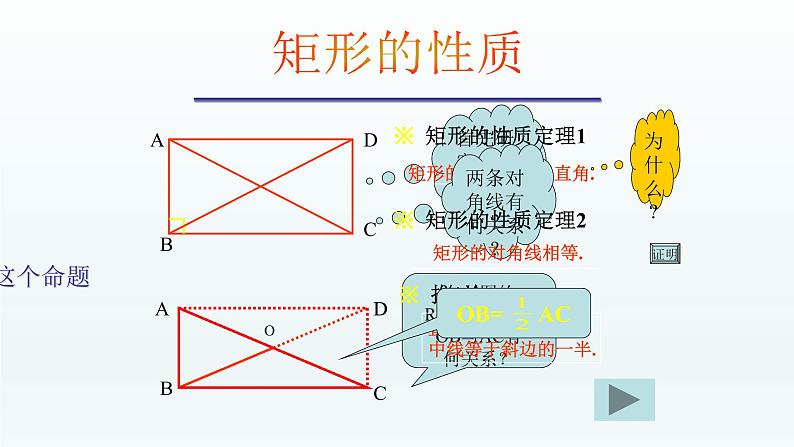
矩形的四个角都是直角.
※ 矩形的性质定理1
※ 矩形的性质定理2
在左图的Rt⊿ABC中，OB与AC有何关系？
直角三角形斜边上的中线等于斜边的一半.
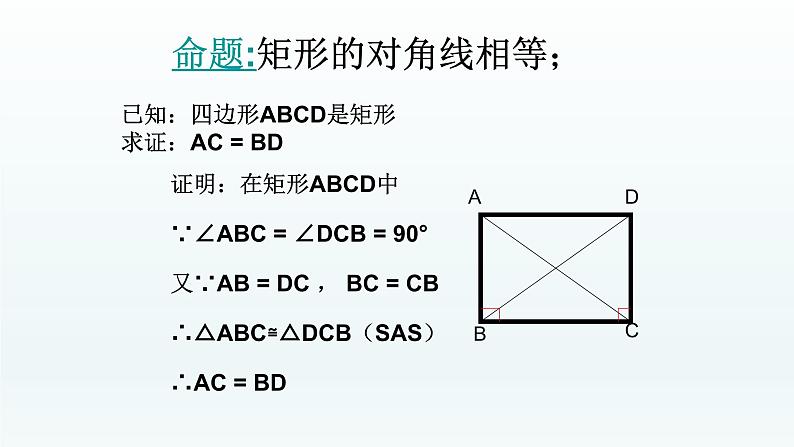
已知：四边形ABCD是矩形 求证：AC = BD
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
∴△ABC≌△DCB（SAS）
命题:矩形的对角线相等；
矩形的四个角都是直角；
矩形的对角线相等且互相平分；
思考：矩形ABCD是轴对称图形吗？
矩形是中心对称图形吗？对称中心是？
例1 如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm,对角线长是13cm，那么矩形的周长是多少？
∵ △AOB、 △BOC、 △COD和△AOD四个三角 形的周长和为86cm，
∴ AC=BD=13cm（矩形的对角线相等）
∴ AB+BC+CD+DA=86－2(AC+BD)
=86－4×13=34(cm)
即矩形ABCD的周长等于34cm。
解： ∵ AC、BD是矩形ABCD的对角线
例2： 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°,AB=4㎝,求矩形对角线的长？
解：∵四边形ABCD是矩形 ∴ OA=OB ∵∠AOB=60° ∴△AOB是等边三角形 ∴OA=AB=4(㎝) ∴矩形的对角线长 AC=BD=2OA=8(㎝)
4、下列性质中，矩形不一定具有的是（ ）A、对角线相等 B、 四个角都相等C、是轴对称图形 D、对角线垂直
1、矩形的定义中有两个条件：一是 ， 二是 。2、有一个角是直角的四边形是矩形。（ ）3、矩形的对角线互相平分。（ ）
5、矩形具有而平行四边形不具有的性 质是（ ） A对角线互相平分 B对角线相等 C两组对边分别平行 D对角相等
6、矩形ABCD中，对角线AC、BD把矩形分成（ ）个等腰三角形，（ ）个全等的直角三角形。（A）2 （B）4 （C）6 （D）8
A D B C
（1）矩形两条对角线的夹角是120度，短边长为4cm。求矩形的对角线长。
（2 ）、已知：矩形ABCD的两条对角线相交于点0，∠AOD=120°， AB =4cm， （1）求矩形对角线的长。（2）求BC边的长。
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
2. 在Rt⊿ABC中，∠C=90°， AB=2AC. 求∠ A 、 ∠B 的度数.
∴⊿ACD是等边三角形
∴∠A=60° ∴∠B=30 °
作BE⊥AC在Rt⊿BCE中，∠ACB=30°
B到AC边距离为____;
⊿ABO是等边三角形，
5. 以2cm和3cm为两条邻边长画一个矩形，并求它的对角线长.
①画AB=3cm，AC=2cm且AB⊥AC，
②作CD∥AB， BD∥AC，交于点D.
四边形ABCD就是所要画的矩形.
矩形的对角线相等且互相平分。
矩形具有平行四边形的所有性质 ；
另外： 矩形的四个内角都是直角。
矩形既是轴对称图形又是中心对称图形 ；
1．下列性质矩形不一定具备的是（ ） A．对角线相等 B．四个内角都相等 C．对角线互相平分 D．对角线互相垂直2．矩形ABCD的长为5，宽为3，点E，F将AC三等分，则△BEF的面积为（ ） A． B． C． D．53．如图，O为矩形ABCD的对角线交点，DF平分∠ADC交AC于E，BC于F，∠BDF=15°，则∠COF=_______．