


人教版八年级下册19.2.2 一次函数示范课ppt课件
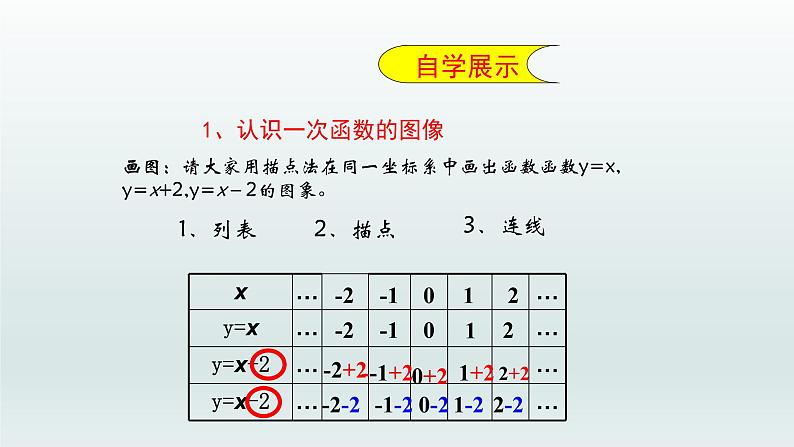
展开画图:请大家用描点法在同一坐标系中画出函数函数y=x, y=x+2,y=x-2的图象。
1、认识一次函数的图像
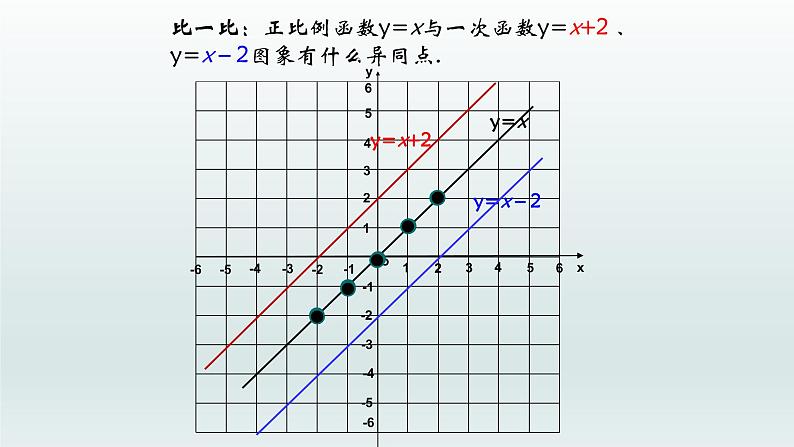
比一比:正比例函数y=x与一次函数y=x+2 、y=x-2图象有什么异同点.
巩固练习(一):1.将直线y=-2x向 平移 单位,可得直线 y=-2x +3的图象;将直线y=-2x向若向 平移 个单位就得到y=-2x -2的图象。
3.直线y=-x+1与直线y=kx+3平行,则k= 4.直线y=-x+1与y轴交点坐标( ),与轴交点坐标( )
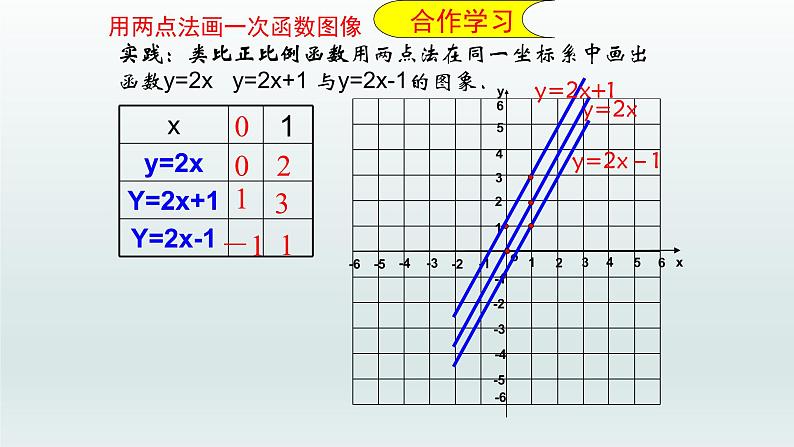
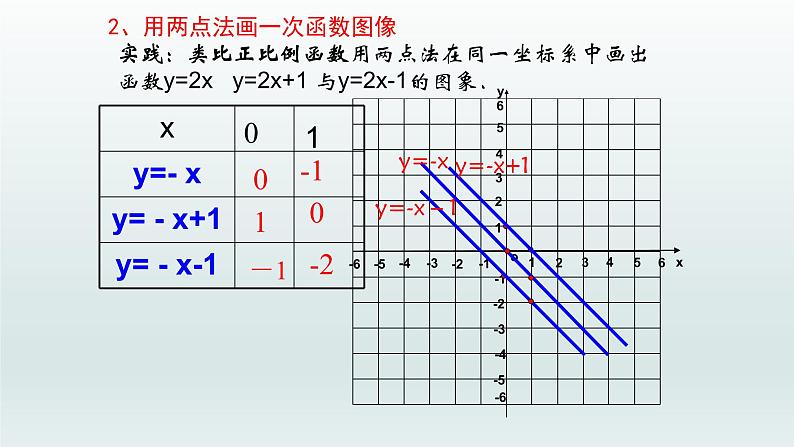
实践:类比正比例函数用两点法在同一坐标系中画出函数y=2x y=2x+1 与y=2x-1的图象.
用两点法画一次函数图像
2、用两点法画一次函数图像
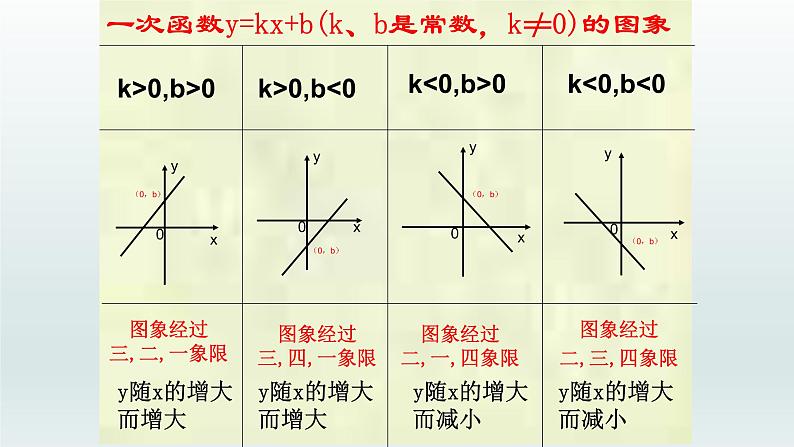
一次函数y=kx+b(k、b是常数,k≠0)的图象
图象经过三,二,一象限
图象经过三,四,一象限
图象经过二,一,四象限
图象经过二,三,四象限
(3) 已知点(-1,a )(2,b)在直线
(4)直线y=2x-3与x轴交点坐标为( )与y轴交点坐标为( ),图象经过 象限,y随x的增大而 ,图象与坐标轴所围成的三角形的面积是
上,则a b的大小关系是
(4)已知一次函数y=kx+b(k≠0)的图象经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数关系式______.
告诉大家本节课你的收获!
3.会用:一次函数的性质
1.会画:用两点法画一次函数的图象
2.会求:一次函数与坐标轴的交点
1.直线y=2x-3与x轴交点坐标为_______,与y轴交点坐标为_____,图象经过第_____象限,y随x增大而_________.2.分别说出满足下列条件的一次函数的图象过哪几个象限? (1)k>0 b>0 (2)k>0 b<0 (3)k<0 b>0 (4)k<0 b<0
3、已知函数y=(m-2)x+n的图象经过一、二、三象限. 求 : m、n的取值范围.
1.下列各点中,那些点在函数y=4x+1的图象上?那些不在函数的图象上? (2, 9) (5,1) (-1,-3) (-0.5,-1)
2.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)两点, 则a= ,b= .
3.点已知M(-3, 4)在一次函数y=ax+1的图象上,则a的值是 .
4、已知某一个函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵点P(3,5)和点Q(-4,-9) 在直线y=kx+b上∴
∴ 一次函数解析式为y=2x-1
5、已知直线y= -2x+4,它与x轴的交点为A,与y轴的交点为B.(1).求A, B两点的坐标.(2).求∆AOB的面积. (O为坐标原点)6、已知某一次函数的图象经过(3, 4), (-2, 0)两点,试求这个一次函数的解析式.
1.有下列函数:①y=2x+1, ②y=-3x+4, ③y=-0.5x,④y=x-6;
(2)函数y随x的增大而增大的是__________;
(1)其中过原点的直线是________;
(3)函数y随x的增大而减小的是___________;
(4)图象在第一、二、三象限的是________ 。
四、巩固提高,达标测试
1. 直线y=2x-3与x轴交点坐标为______;与y轴的交点坐标为______;图象经过________象限,y随x的增大而___.2.若此直线平行于直线y=-3x-5,则k= .3. 直线y=2x-3的图象经过点 (0, )与点( ,0),图像经过___象限,y 随x的增大而 。
排“兵”布阵 抢答题
1(09湖南邵阳)在平面直角坐标系中,函数y=-2x+3的图象经过( )A.一、二、三象限 B.二、三、四象限C.一、三、四象限 D.一、二、四象限
2(2009宁夏)5.一次函数y=3x-2的图象不经过( )A.第一象限 B.第二象限 C.第三象限 D.第四象限
3(2009年株洲市)一次函数y=2x+1的图象不经过( )A.第一象限 B.第二象限C.第三象限D.第四象限
2009年重庆市江津区)已知一次函数y=x-2的大致图像为 ( )
A B C D
1 函数y=3x-4经过 象限
3一次函数y = (m-3)x+m+1的图象经过一、二、四象限,则正整数m= ________.
2一次函数y=-x-5的图像不经过____象限
4根据一次函数的图象,说出解析式y=kx+b中k与b的取值范围.K 0, b 0,
逆向思维 小试牛刀已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
例、已知:一次函数 y=(5m-3)x+(2-n).(1)当 m 为何值时,y 随 x 的增大而减小;(2)当 m、n 分别为何值时,一次函数与 y 轴的交点在 x 轴的上方?
练习: 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:(1)函数值y 随x的增大而增大;(2)函数图象与y 轴的负半轴相交;(3)函数的图象过第二、三、四象限;(4)函数的图象不过第一象限
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗? 它们图象之间有什么关系?一次函数又有什么性质呢?
观察:比较上面三个函数的相同点与不同点,根据你的观察结果回答下列问题:
(1)这三个函数的图象形状都是___,并且倾斜程度___;(2)函数y=x图象经过原点,一次函数y=x+2 的图象与y轴交于点____,即它可以看作由直线y=x向__平移__单位长度而得到;一次函数y=x-2的图象与y轴交于点____,即它可以看作由直线y=x向__平移__单位长度而得到;
总结:画一次函数的图像时,只要描出合适关系式的两点,再连接两点即可,我们通常选 取(0,)和( ,k)
y=kx+b(k,b是常数,k≠0)
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
经过一、三象限y随x增大而增大
经过二、四象限y随x增大而减小
3、正比例函数 y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响?
体验:在同一坐标系中用两点法画出函数y=x+1,y=-x+1,y=2x+1y=-2x+1 的图象.
探究:观察上面四个一次函数的图象,类比正比例函数y=kx中k的正负对图象的影响,表述一次函数的性质.
当K>0时,图象从左到右上升,y随x增大而增大
当K<0时,图象从左到右下降,y随x增大而减小
k 决定直线的倾斜程度和方向
继续探究: 在同一直角坐标系中画出下列函数图象,并归纳y=kx+b(k、b是常数,k≠0)中b对函数图象的影响.1.y=x-1 y=x y=x+12.y=-2x+1 y=-2x y=-2x-1
当b>0时,交点在原点上方. 当b=0时,交点即原点.当b<0时,交点在原点下方.
直线y=kx+b与y轴交点的坐标( ).
b 决定直线与y轴交点位置
4.当 b相等时,直线交于y轴上同一点
(1) 所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx___________而得到
当b>0,向上平移b个单位;当b<0,向下平移b个单位。
※※※一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度而得到(当b>0,向上平移;当b<0时,向下平移)。
初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数精品ppt课件: 这是一份初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数精品ppt课件,共19页。PPT课件主要包含了复习旧知,y-6x+5,y-6x,合作探究一,ykx+b,ykx,合作探究二,y2x-1,合作探究三,巩固练习等内容,欢迎下载使用。
人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数获奖课件ppt: 这是一份人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数获奖课件ppt,共17页。PPT课件主要包含了一回顾与思考,kx+b,一次函数,正比例函数y,图象的特征,从左向右看图象___,y随x的增大而___,图象的性质,二创设问题,猜一猜等内容,欢迎下载使用。
初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数优质ppt课件: 这是一份初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数优质ppt课件,共16页。PPT课件主要包含了练一练,大显身手等内容,欢迎下载使用。













