
































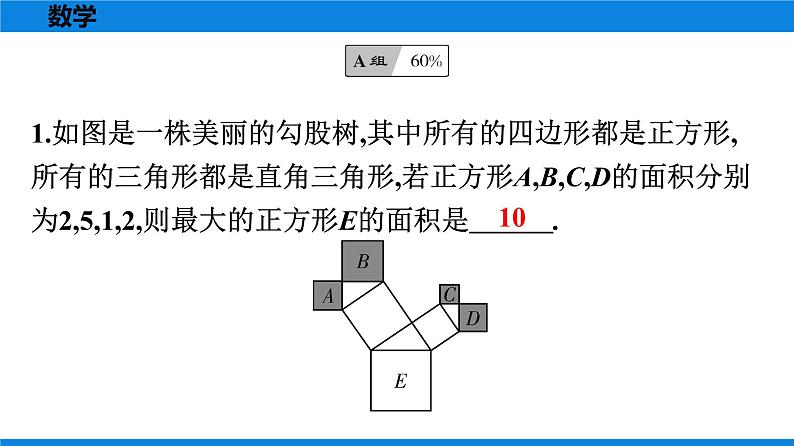
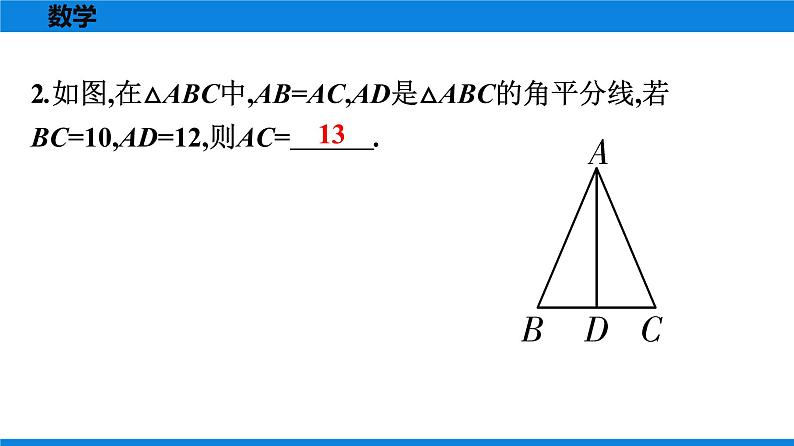
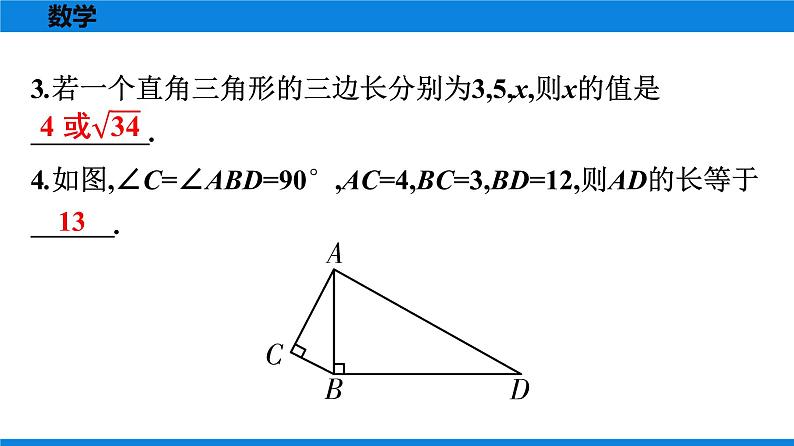
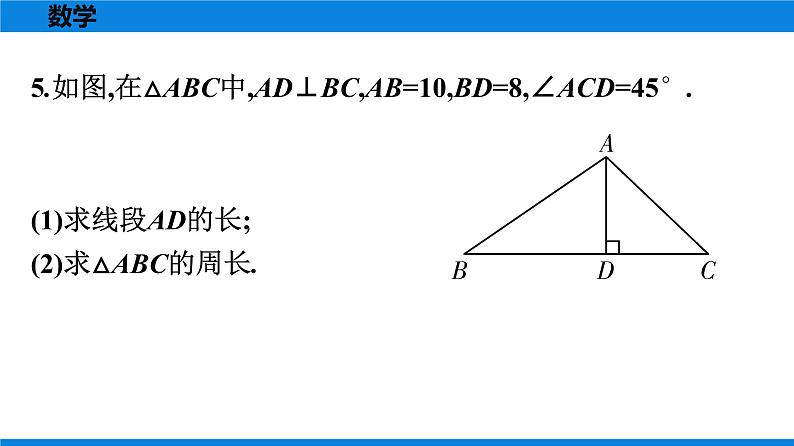


所属成套资源:人教版数学八年级下册全册教学PPT课件+课时作业+期末知识复习
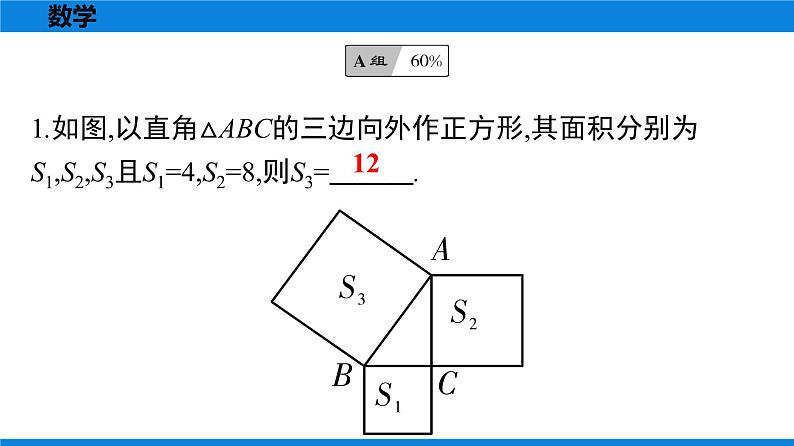
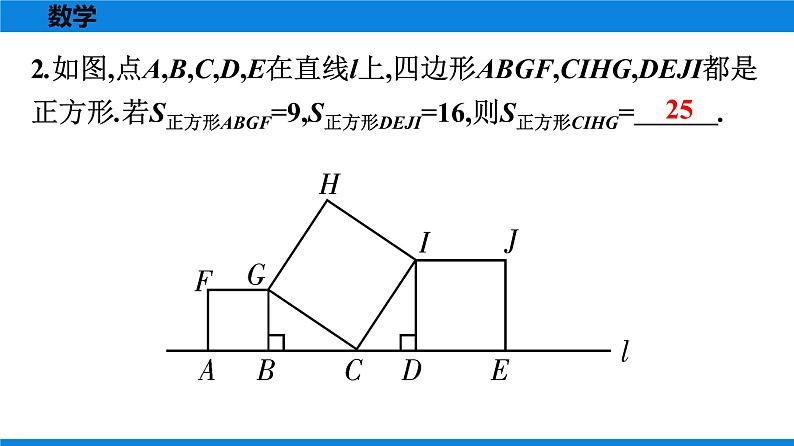
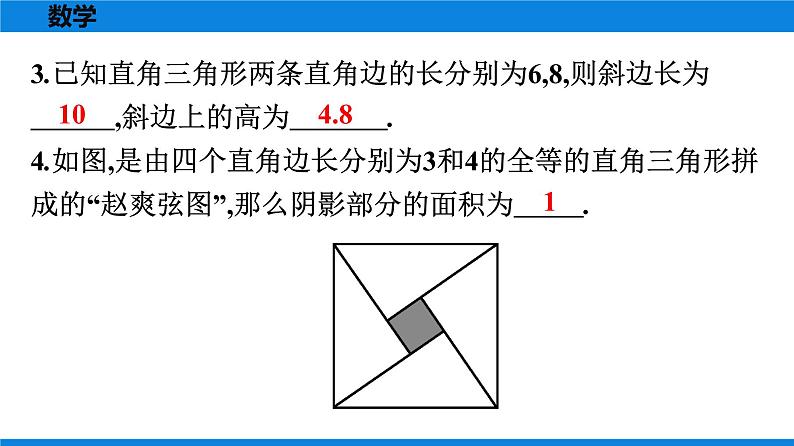
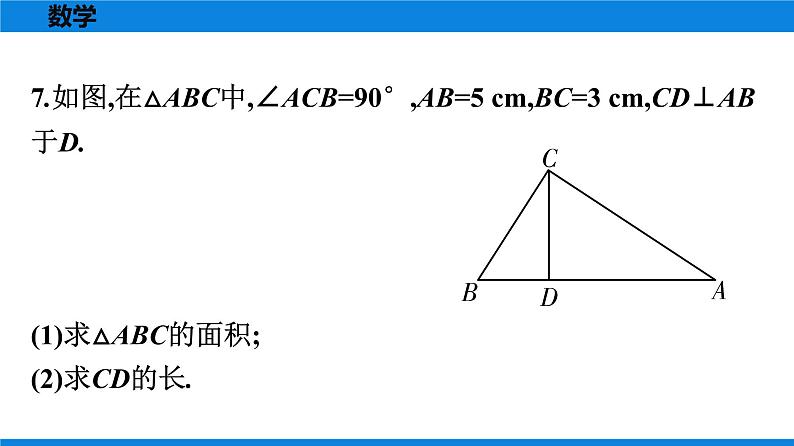
人教版八年级下册17.1 勾股定理公开课作业课件ppt
展开
这是一份人教版八年级下册17.1 勾股定理公开课作业课件ppt,文件包含第1课时勾股定理1pptx、第2课时勾股定理2pptx、第3课时勾股定理3pptx、第4课时勾股定理的逆定理1pptx、第5课时勾股定理的逆定理2pptx、第6课时《勾股定理》单元复习pptx等6份课件配套教学资源,其中PPT共109页, 欢迎下载使用。
1.若8,a,17是一组勾股数,则a= . 2.若△ABC的三边a,b,c满足(a-b)(a2+b2-c2)=0,其中a≠b,则△ABC的形状为 . 3.若△ABC的三边长分别为x+1,x+2,x+3,其中x>0.要使此三角形成为直角三角形,则x= .
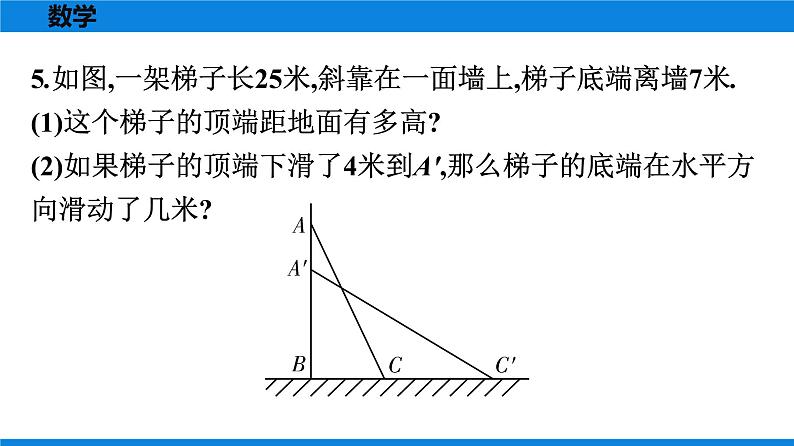
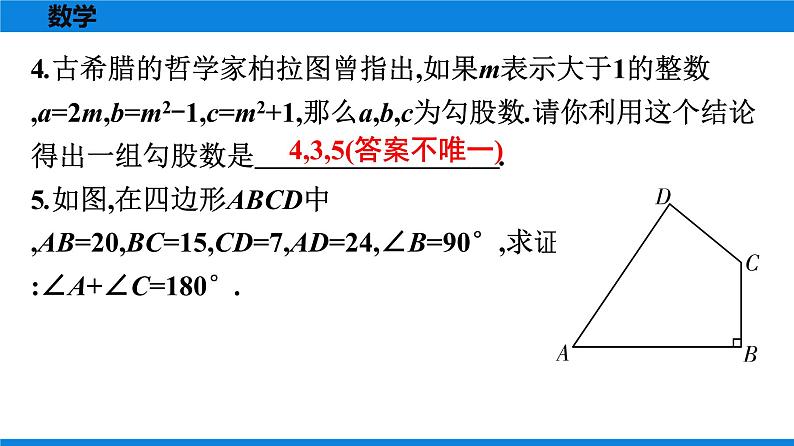
4.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.请你利用这个结论得出一组勾股数是 . 5.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
4,3,5(答案不唯一)
证明:连接AC.∵AB=20,BC=15,∠B=90°,∴由勾股定理,得AC2=202+152=625.又CD=7,AD=24,∴CD2+AD2=625,∴AC2=CD2+AD2,∴∠D=90°.∴∠A+∠C=360°-180°=180°.
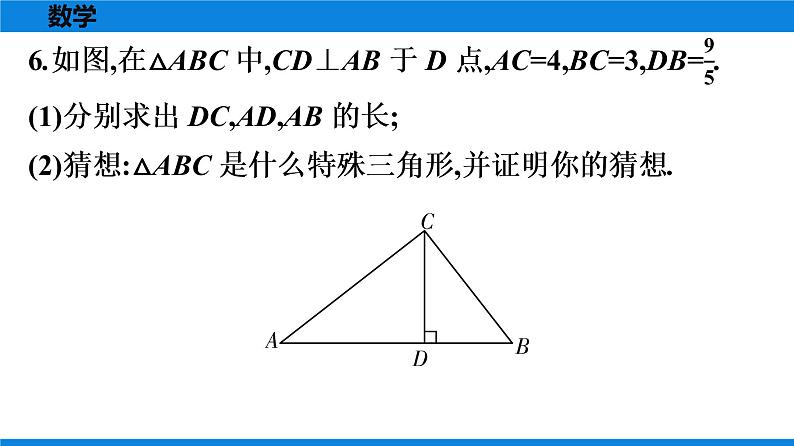
(2)猜想:△ABC是直角三角形.证明如下:∵在△ABC中,AC=4,BC=3,AB=5,∴AC2+BC2=42+32=52=AB2,∴△ABC是直角三角形.
7.在寻找马航MH370航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A,B.接到消息后,一艘舰艇以16海里/时的速度离开港口O(如图)向北偏东40°方向航行,另一艘舰艇同时以12海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30海里,问另一艘舰艇的航行方向是北偏西多少度?
解:由题意得OB=12×1.5=18海里,OA=16×1.5=24海里,又∵AB=30海里,∵182+242=302,即OB2+OA2=AB2,∴∠AOB=90°,∵∠DOA=40°,∴∠BOD=50°,则另一艘舰艇的航行方向是北偏西50°.
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= ,b= ,c= ; (2)猜想:以a,b,c为边的三角形是否为直角三角形,并证明你的猜想.
解:(2)猜想为以a,b,c为边的三角形是直角三角形.证明:∵a=n2-1,b=2n,c=n2+1,∴a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1=(n2+1)2,而c2=(n2+1)2,∴根据勾股定理的逆定理可知以a,b,c为边的三角形是直角三角形.
10.如图是一块四边形木料,木工师傅按规定做得∠ABC=90°,AB=3,BC=4, CD=12,AD=13,你能帮木工师傅计算一下这块木料的面积吗?
11.如图,在△ABC中,AD是BC边上的高,且AD2=BD·CD.求证:△ABC是直角三角形.
证明:∵Rt△ABD中,AB2=BD2+AD2,在Rt△ACD中,AC2=CD2+AD2,∴AB2+AC2=BD2+2AD2+CD2.又∵AD2=BD·CD,∴AB2+AC2=BD2+2BD·CD+CD2=(BD+CD)2=BC2,∴△ABC是直角三角形.
相关课件
这是一份人教版八年级下册17.1 勾股定理作业ppt课件,共18页。
这是一份数学人教版17.2 勾股定理的逆定理作业ppt课件,共7页。
这是一份初中数学人教版八年级下册17.2 勾股定理的逆定理作业课件ppt,共20页。PPT课件主要包含了知识点3勾股数,归纳总结等内容,欢迎下载使用。









