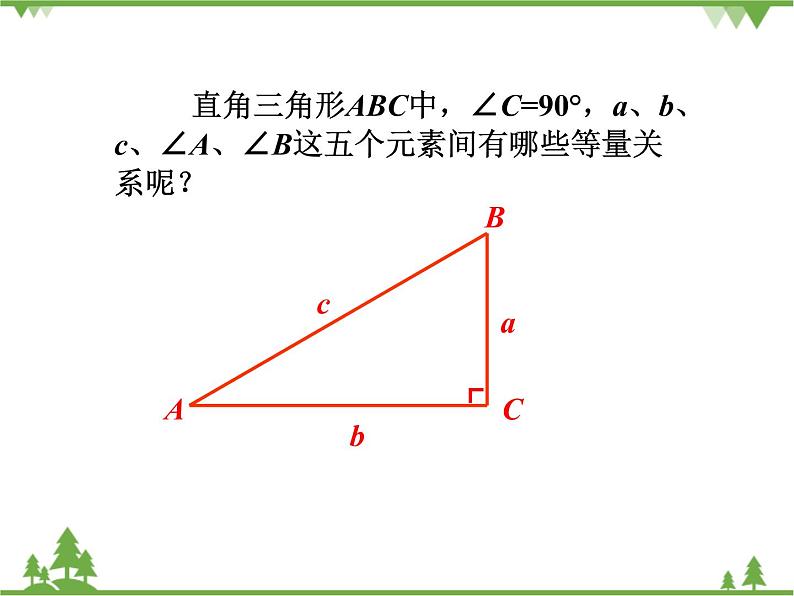
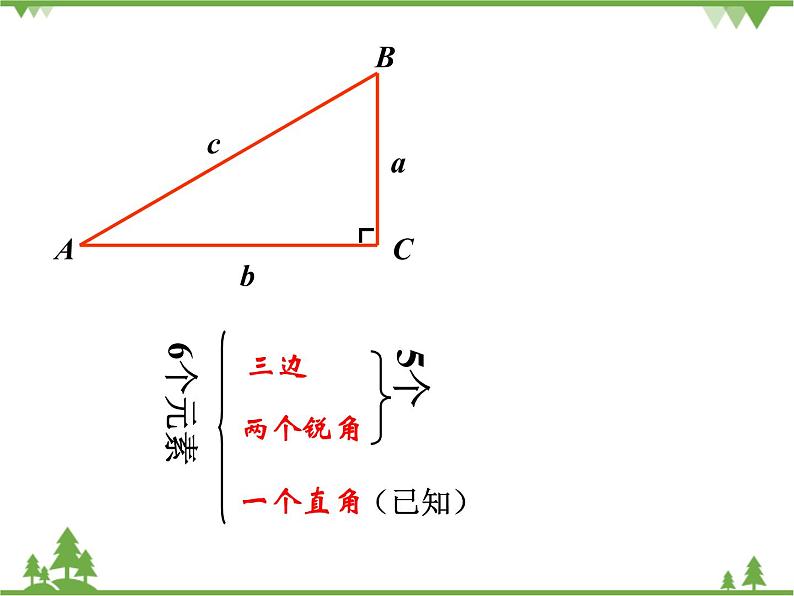
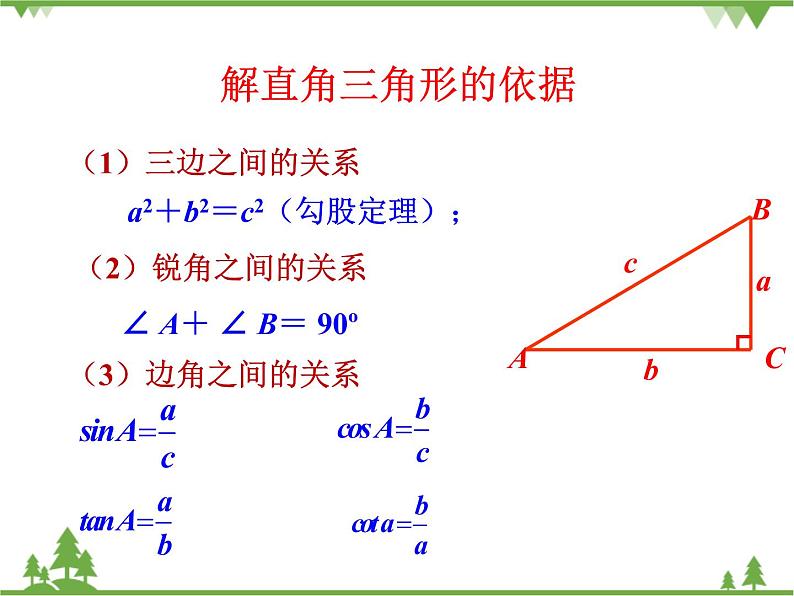
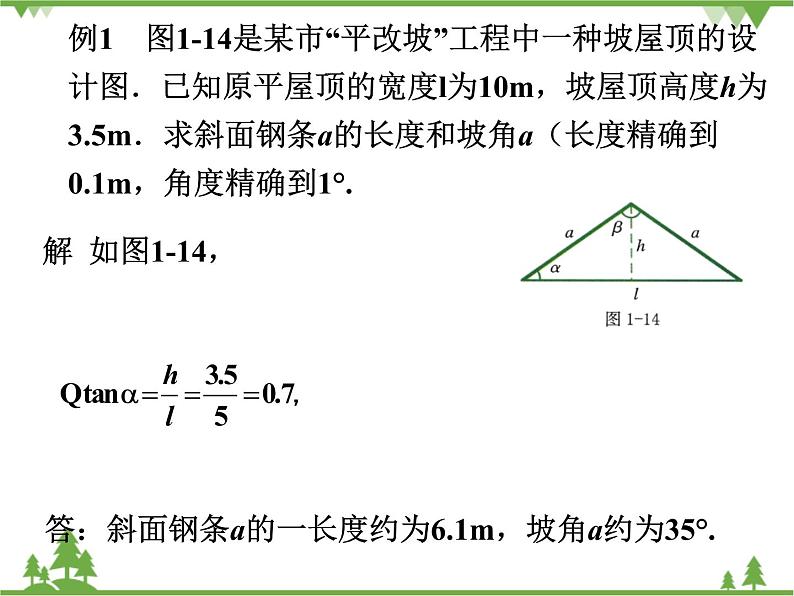
初中浙教版1.3 解直角三角形优秀备课作业ppt课件

第1章   锐角三角函数

1.3   解直角三角形

一、单选题

1．如图，某地修建高速公路，要从地向地修一条隧道（点在同一水平面上）．为了测量两地之间的距离，一架直升飞机从地出发，垂直上升米到达处，在处观察地的俯角为，则两地之间的距离为（    ）

A．米 B．米 C．米 D．米

【答案】D

【分析】

由题意知∠BAC=90°，∠ABC=30°，AC=800米，由tan∠ABC=，即可求解．

【详解】

由题意知∠BAC=90°，∠ABC=30°，AC=800米，
∵tan∠ABC=，

∴AB(米)，

故选：D．

【点睛】

本题主要考查了解直角三角形的应用-仰角俯角问题，解题的关键是熟练掌握基本知识，属于中考常考题型．

2．周末小李带妹妹游览校园，如图所示，在学校门口点观察到刻有校名的牌坊底部的仰角为24°，牌坊顶部的仰角为39°，测得斜坡的坡面距离，斜坡的坡度．则牌坊的高度是（    ）米．（参考数据，，；，；结果保留到0.1）

A．11.7 B．12.8 C．15.6 D．24.0

【答案】B

【分析】

由斜坡BC的坡度i=8：15设CE=8x、BE=15x，由BC=17x=34，求得x=2，据此知AE、DE的长，再根据DC=DE-CE，可得答案．

【详解】

解：由斜坡 的坡度设，

则，

解得，

米，米，

在中，（米），

在中，（米），

则（米），

故选：B．

【点睛】

本题主要考查解直角三角形的应用能力，注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键．

3．如图，一艘轮船从位于灯塔C的北偏东方向，距离灯塔60海里的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东方向上的B处，这时轮船B与小岛A的距离是(　　)

A．海里 B．海里 C．120海里 D．60海里

【答案】B

【分析】

过点C作CD⊥AB于点D，先解Rt△ACD，求出AD，CD，再根据BD=CD，即可解出AB．

【详解】

如图，过点C作CD⊥AB于点D，

则∠ACD=30°，∠BCD=45°，

在Rt△ACD中，AD=CA=×60=30（海里），

CD=CA·cos∠ACD=60×=（海里），

∵∠BCD=45°，∠BDC=90°，

∴在Rt△BCD中，BD=CD，

∴AB=AD+BD=AD+CD=（30+）海里，

故选：B．

【点睛】

此题主要考查了解直角三角形的应用——方向角问题，解一般三角形的问题，一般可以转化为解直角三角形的问题，解题的关键是作高线．

4．如图是一个根据北京的地理位置设计的圭表，其中立柱高为 .已知冬至时重庆的正午日光入射角，则立柱根部与圭表的冬至线的距离（即的长）约为（　 ）

A． B． C． D．

【答案】B

【分析】

根据题意和图形，通过∠ABC的正切值可以用含a的式子表示出BC的长，从而可以解答本题．

【详解】

解：由题意可得，

在Rt△ABC中，tan∠ABC=，

∴tan28.2°=，

∴，

故选：B．

【点睛】

本题考查解直角三角形的应用，解答本题的关键是明确题意，利用锐角三角函数解答．

5．如图，一个木块沿着倾斜角为的斜坡，从滑行至巳知米，则这个木块的高度约下降了（参考数据：，，）（    ）

A．3．65米 B．3．40米 C．3．35米 D．3．55米

【答案】A

【分析】

过点A作AC垂直于水平线，交于点C，构造，解直角三角形，求出AC，AC即木块下降的高度.

【详解】

本题考查三角函数的定义．过点作水平面的垂线，垂足为，则，故（米），故选A．

【点睛】

本题主要考查了解直角三角形的应用，作出辅助线构造直角三角形是解题的关键.

6．下表是小丽填写的实践活动报告的部分内容：

设树顶端到地面的高度为，根据以上条件，可以列出求树高的方程为（   ）

A． B．

C． D．

【答案】C

【分析】

根据三角函数的定义列方程即可得到结论．

【详解】

∵∠DAC=45°，
∴AC=CD=，
∵AB=10，
∴BC=，
∴tan56°=，
∴，
故选：C．

【点睛】

本题考查了解直角三角形的应用，由实际问题抽象出一元一次方程，正确的识别图形是解题的关键．

7．如图，一个小球由地面沿着坡角为30°的坡面向上前进了10m，此时小球距离地面的高度为（    ）

A．5m B．m C． D．

【答案】A

【分析】

首先画出符合题意的直角△ABC，再根据坡角的定义可知∠A=30°，然后利用正弦函数的定义即可求解．

【详解】

如图，

∵直角△ABC中，∠C=90°，∠A=30°，AB=10，
∴()，
故选：A．

【点睛】

本题考查了解直角三角形的应用-坡度坡角问题，正弦函数的定义，理解坡角的定义，进而画出符合题意的直角△ABC是解决本题的关键．

8．一辆汽车在坡角为的坡面上行驶1000米，则它上升的高度为（    ）米

A． B． C． D．

【答案】D

【分析】

利用坡角的正弦值即可求解．

【详解】

解：如图，∠A=α，AE=1000．

则EF=1000sinα．

故选：D．

【点睛】

此题主要考查学生对坡度坡角的掌握情况及三角函数的运用．

二、填空题

9．有一轮船由东向西航行，在处测得西偏北有一灯塔，继续航行10海里后到处，又测得灯塔在西东偏北，如果轮船航向不变，则灯塔与船之间的最近距离是__________海里．

【答案】5

【分析】

过点P作PC⊥AB于点C，求出 PB=AB=10，再用三角函数求解即可．

【详解】

解：如图，过点P作PC⊥AB于点C，

∵∠PBC=30°,∠PAB=15°,

∴∠BPA=15°,

∴PB=AB=10,

∴PC=PB sin30°=5.

故答案为5．

【点睛】

本题通过考查仰角的定义，构造直角三角形求解．考查了学生读图构造关系的能力．

10．如图，某商场停车场门口的柱子上方挂着一块收费标准牌，收费标准牌的一侧用绳子和牵引着两排小彩旗，经过测量得到如下数据：米，米，，，则的长度为______米．（结果保留根号）

【答案】

【分析】

直接根据题意得出DM的长，再求出BM，根据正切函求得CM的长，进而得出答案．

【详解】

在Rt△AMD中，∠MAD=45°，
∴DM=AM=4（m），
在Rt△BMC中，∠MBC=30°，
∴CM=BM⋅tan30°，
∵BM=AM+AB=4+8=12（m），
∴CM=12，

∴CD=CM-DM=（米），
答：警示牌的高CD为()米．

故答案为：．

【点睛】

本题考查了解直角三角形的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用特殊角的三角函数解答．

11．如图，在点处测得塔顶的仰角为，点到塔底的水平距离是，那么塔的高度为_________（用含的式子表示）.

【答案】

【分析】

根据三角函数的定义和直角三角形的性质解答即可．

【详解】

解：∵在点B处测得塔顶A的仰角为，

∴∠B＝，

∵BC＝30m，

∴AC＝BC•tan＝30tan，

故答案为30tan．

【点睛】

此题考查了解直角三角形−仰角的定义，注意方程思想与数形结合思想的应用．

12．如图，在Rt△ABC中，AB的垂直平分线交BC边于点E.若BE=2，∠B =22.5°，则AC的长为_______．

【答案】

【分析】

先根据线段垂直平分线的性质得出AE=BE=2，故∠EAB=∠B=22.5°，由三角形外角的性质得出∠AEC的度数，再根据锐角三角函数的定义即可得出结论．

【详解】

解：∵AB的垂直平分线交BC边于点E，BE=2，∠B=22.5°
∴AE=BE=2，
∴∠EAB=∠B=22.5°．
∵∠AEC是△ABE的外角，
∴∠AEC=∠B+∠EAB=45°．
∵∠C=90°，
∴AC=AE•sin45°=2×=．
故答案为：．

【点睛】

本题考查的是线段垂直平分线的性质，解直角三角形，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．

13．如图，是某高速公路边水平地面上的交通警示牌，经测量得到如下数据：，，，，，则警示牌的高度为_________．（结果精确到，参考数据：，）

【答案】

【分析】

在Rt△CAD中求出CD，在Rt△CBE中求出CE即可解决问题．

【详解】

解：在Rt△CAD中，∵∠DCA=90°，AC=AB+BC=12m，∠DAC=30°，
∴CD=AC •tan30°=12×=≈6.92，
在Rt△CBE中，∵∠ECB=90°，∠EBC=45°，
∴∠CEB=∠EBC=45°，
∴CE=CB=4m，
∴DE=CD-CE=6.92-4=2.92≈，
故答案为：

【点睛】

此题主要考查了解直角三角形的应用，正确得出CD，CE的长是解题关键．

14．如图，一根竖直的木杆在离地面2.1m处折断，木杆顶端落在地面上，且与地面成38°角，则木杆折断之前高度约为________m．（结果保留一位小数）（参考数据：sin38°≈0.62，cos38°≈0.79，tan38°≈0.78） 

【答案】5.5

【分析】

由题意可知：BC=2.1，∠A=38°，根据锐角三角函数的定义即可求出答案．

【详解】

解：如图，

由题意可知：BC=2.1，∠A=38°，
∴，
∴AB=≈3.4，
∴AB+BC≈3.4+2.1=5.5，
故答案为：5.5

【点睛】

本题考查解直角三角形，解题的关键是熟练运用锐角三角函数的定义，本题属于基础题型．

三、解答题

15．如图，斜坡BE，坡顶B到水平地面的距离AB为3米，坡底AE为16米，在B处，E处分别测得CD顶部点D的仰角为30°，60°，求CD的高度．

【答案】CD的高度为 米．

【分析】

作BF⊥CD于点F，设DF＝x米，在直角△DBF中利用三角函数用x表示出BF的长，在直角△DCE中表示出CE的长，然后根据BF−CE＝AE即可列方程求得x的值，进而求得CD的长．

【详解】

作BF⊥CD于点F，设DF＝x米，

在Rt△DBF中，tan∠DBF＝，

则BF＝，

在直角△DCE中，DC＝x＋CF＝3＋x（米），

在直角△DCE中，tan∠DEC＝，则EC＝米．

∵BF−CE＝AE，即x−＝16．

解得：x＝，

则CD＝＋3＝（米）．

答：CD的高度是（）米．

【点睛】

本题考查了解直角三角形的应用，解答本题关键是构造直角三角形，利用三角函数的知识表示出相关线段的长度．

16．如图，天空中有一个静止的广告气球C，从地面A点测得C点的仰角为45°，从地面B点测得C点的仰角为60°．已知AB＝20m，点C和直线AB在同一铅垂平面上，求气球离地面的高度（结果保留根号）．

【答案】10（3＋）米

【分析】

过点C作CD⊥AB，交AB于点D；设CD＝x．本题涉及到两个直角三角形△ADC、△BDC，应利用其公共边CD构造等量关系，解三角形可得AD、BD与x的关系；借助AB＝AD−BD构造方程关系式，进而可求出答案．

【详解】

过点C作CD⊥AB，交AB于点D；设CD＝x，

在Rt△ADC中，有AD＝CD/ tan45＝CD＝x，

在Rt△BDC中，有BD＝CD/ tan60＝x，

又有AB＝AD−BD＝20；即x−x＝20，

解得：x＝10（3＋），

答：气球离地面的高度CD为10（3＋）米．

【点睛】

本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．

17．如图，无人机在空中处测得地面、两点的俯角分别为60〫、45〫，如果无人机距地面高度米，点、、在同水平直线上，求、两点间的距离．（结果保留根号）

【答案】A、B两点间的距离为100（1+）米

【分析】

如图，利用平行线的性质得∠A=60°，∠B=45°，在Rt△ACD中利用正切定义可计算出AD=100，在Rt△BCD中利用等腰直角三角形的性质得BD=CD=100，然后计算AD+BD即可．

【详解】

∵无人机在空中C处测得地面A、B两点的俯角分别为60°、45°，

∴∠A=60°，∠B=45°，

在中，∵=，

∴AD==100，

在中，BD=CD=100，

∴AB=AD+BD=100+100=100(1+)．

答：A、B两点间的距离为100(1+)米．

【点睛】

本题考查了解直角三角形的应用-仰角俯角问题：解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作高或垂线构造直角三角形．

18．一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，

（1）求点C到直线AB的距离；

（2）求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）

【答案】（1）40海里；（2）小时．

【分析】

（1）作CD⊥AB，在Rt△ACD中，由∠CAD＝30°知CD＝AC，据此可得答案；

（2）根据BC＝求得BC的长，继而可得答案．

【详解】

解：（1）如图，过点C作CD⊥AB交AB延长线于D．

在Rt△ACD中，∵∠ADC＝90°，∠CAD＝30°，AC＝80海里，

∴点C到直线AB距离CD＝AC＝40(海里）．

（2）在Rt△CBD中，∵∠CDB＝90°，∠CBD＝90°﹣37°＝53°，

∴BC＝≈＝50（海里），

∴海警船到达事故船C处所需的时间大约为：50÷40＝（小时）．

【点睛】

此题主要考查解直角三角形的应用，解题的关键是熟知三角函数的定义.

19．如图，在5X5的正方形网格中，每个小正方形的边长均为，线段的端点均在小正方形的顶点上，请按要求画出图形并计算:

以为一边画出，使其是等腰直角三角形，点在小正方形的顶点上，且的面积为；

以为一边画出，使得，点在小正方形的顶点上，且的面积最大；

连接，并直接写出四边形的面积．

【答案】（1）详见解析；（2）详见解析；（3）10

【解析】

【分析】

（1）根据网格的特点求出AB=，根据面积为5求出直角边为，故可画出；

（2）根据，根据网格的特点确定E，再根据三角形面积最大即BD最长，故可画出；

（3）根据网格的特点利用割补法即可求解．

【详解】

如图，为所求；

如图，为所求；

S=5×5-2×1×2-2××1×3-2××2×4=25-4-3-8=10．

【点睛】

此题主要考查网格与等腰三角形、三角函数的应用，解题的关键是熟知等腰三角形的性质、正切的定义及网格的特点．

20．如图，在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，求∠A的正弦值、余弦值和正切值．

【答案】sinA=，cosA=，tanA=．

【分析】

根据勾股定理求出AB，根据锐角三角函数的定义解答即可．

【详解】

由勾股定理得，，

则，，．

【点睛】

本题考查解直角三角形，解题的关键是利用勾股定理求出AB的长.