



还剩7页未读,
继续阅读
初中数学沪科版八年级上册12.2 一次函数优秀ppt课件
展开
这是一份初中数学沪科版八年级上册12.2 一次函数优秀ppt课件,共13页。PPT课件主要包含了1填出下表,解1填表,函数图像如图所示,y5x,y4x+2,②画出上述函数图象,收获乐园,能力提升2,y3x,y-x+8等内容,欢迎下载使用。
分析:本题y随x变化的规律分成两段:前5分钟与后10分钟.写y 随x变化函数关系式时要分成两部分.画图象时也要分成两段来画,且要注意各自变量的取值范围.
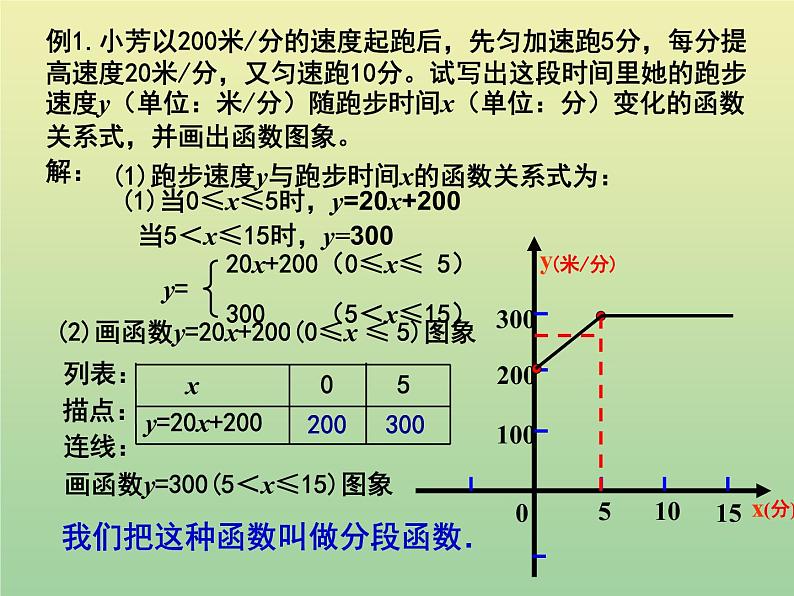
例1.小芳以200米/分的速度起跑后,先匀加速跑5分,每分提高速度20米/分,又匀速跑10分。试写出这段时间里她的跑步速度y(单位:米/分)随跑步时间x(单位:分)变化的函数关系式,并画出函数图象。
(1)跑步速度y与跑步时间x的函数关系式为:
(2)画函数y=20x+200(0≤x ≤ 5)图象
画函数y=300(5<x≤15)图象
我们把这种函数叫做分段函数.
(1)当0≤x≤5时,y=20x+200
当5<x≤15时,y=300
分析:付款金额与种子价格相关,问题中的种子价格不是固定不变的,它与购买种子数量有关,设购买x千克种子,当0≤x≤2时,种子价格为5元/千克;当x>2时,其中有2千克种子按5元/千克计算,其余的(x-2)千克(即超出2千克部分)种子按4元/千克(即8折)计价.因此,写函数解析式与画函数图像时,应对0≤x≤2 和x>2分段讨论.
例2.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打8折.
(2)写出购买种子数量与付款金额之间的函数解析式,并画出函数的图像.
(2)设购买种子数量为x千克,付款金额为y元.
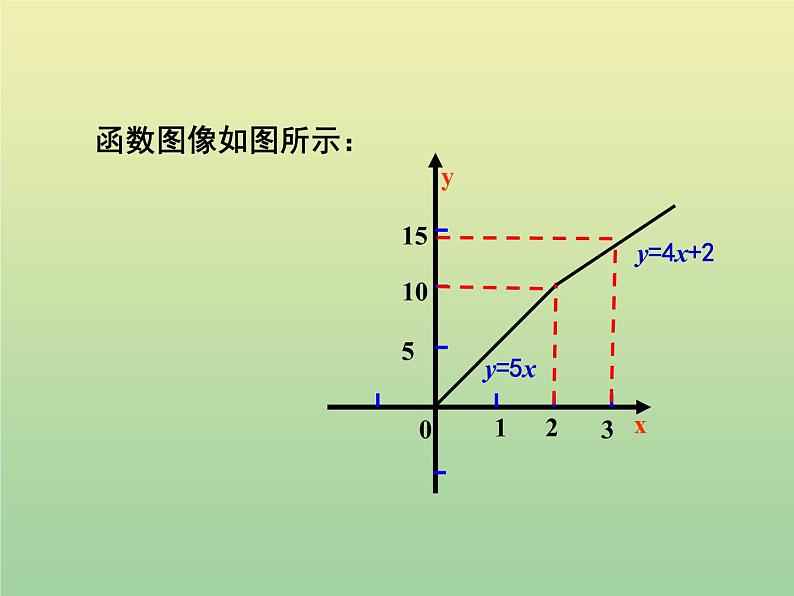
当0≤x≤2时,y=5x.
当x>2时,y=4(x-2)+10
即 y=4x+2
例3.为节约用水,某城市制定以下用水收费标准:每户每月用水不超过8m³时,每m³收取1元外加0.3元的污水处理费;超过8m³时,每m³收取1.5元外加1.2元的污水处理费.设一户每月用水量为xm³,应缴水费y元.
①给出y与x之间的函数表达式;
③当该市一户某月的用水量为5m³或10m³时,求其应缴的水费;
④该市一户某月缴水费26.6元,求该户这个月用水量.
为了加强公民的节水意识,某城市规定用水收费标准如下:每户每月用水量不超过6米3时,水费按0.6元/米3收费,超过6米3时,超过部分每米3按1元收费,每户每月用水量为x米3,应缴水费y元.
(1)写出每月用水量不超过6米3和超过6米3时,y与x之间的函数关系式.(2)已知某户5月份用水量为8米3,求该用户5月份的水费。
(1)当0≤x≤6时,y = 0.6x.
当x>6时,y = 0.6×6 + 1×(x -6)
即 y = x -2.4
(2)当x=8时,y = 8 - 2.4 = 5.6
故,该用户5月份的水费为5.6元.
(3)数学与生活、生产实际有密切联系,我们碰到实际问题要善于用数学方法去分析、去解决,看到数学的函数图像也要善于给它赋予不同的意义,这是学好数学的秘诀之一。
(1)识别、分析函数图像所描述的信息;
2.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药(1)服药后____时,血液中含药量最高,达到每毫升_______毫克。(2)服药5时,血液中含药量为每毫升____毫克。(3)当x≤2时,y与x之间的函数关系式是_____。(4)当x≥2时,y与x之间的函数关系式是_________。(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是___ 小时。.
点评(1)根据图像反映的信息解答有关问题时,首先要弄清楚两坐标轴的实际意义,抓住几个关键点来解决问题;(2)特别注意,第5问中由y=3对应的x值有两个;(3)根据函数图像反映的信息来解答有关问题,比较形象、直观,从中能进一步感受“数形结合思想”。
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药的一定时间内每毫升血液中含药量y(微克)随时间x(时)逐步增加,变化情况如图所示.
(1)当0≤ x≤2时,y与x之间的函数关系式是 。
分析:本题y随x变化的规律分成两段:前5分钟与后10分钟.写y 随x变化函数关系式时要分成两部分.画图象时也要分成两段来画,且要注意各自变量的取值范围.
例1.小芳以200米/分的速度起跑后,先匀加速跑5分,每分提高速度20米/分,又匀速跑10分。试写出这段时间里她的跑步速度y(单位:米/分)随跑步时间x(单位:分)变化的函数关系式,并画出函数图象。
(1)跑步速度y与跑步时间x的函数关系式为:
(2)画函数y=20x+200(0≤x ≤ 5)图象
画函数y=300(5<x≤15)图象
我们把这种函数叫做分段函数.
(1)当0≤x≤5时,y=20x+200
当5<x≤15时,y=300
分析:付款金额与种子价格相关,问题中的种子价格不是固定不变的,它与购买种子数量有关,设购买x千克种子,当0≤x≤2时,种子价格为5元/千克;当x>2时,其中有2千克种子按5元/千克计算,其余的(x-2)千克(即超出2千克部分)种子按4元/千克(即8折)计价.因此,写函数解析式与画函数图像时,应对0≤x≤2 和x>2分段讨论.
例2.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打8折.
(2)写出购买种子数量与付款金额之间的函数解析式,并画出函数的图像.
(2)设购买种子数量为x千克,付款金额为y元.
当0≤x≤2时,y=5x.
当x>2时,y=4(x-2)+10
即 y=4x+2
例3.为节约用水,某城市制定以下用水收费标准:每户每月用水不超过8m³时,每m³收取1元外加0.3元的污水处理费;超过8m³时,每m³收取1.5元外加1.2元的污水处理费.设一户每月用水量为xm³,应缴水费y元.
①给出y与x之间的函数表达式;
③当该市一户某月的用水量为5m³或10m³时,求其应缴的水费;
④该市一户某月缴水费26.6元,求该户这个月用水量.
为了加强公民的节水意识,某城市规定用水收费标准如下:每户每月用水量不超过6米3时,水费按0.6元/米3收费,超过6米3时,超过部分每米3按1元收费,每户每月用水量为x米3,应缴水费y元.
(1)写出每月用水量不超过6米3和超过6米3时,y与x之间的函数关系式.(2)已知某户5月份用水量为8米3,求该用户5月份的水费。
(1)当0≤x≤6时,y = 0.6x.
当x>6时,y = 0.6×6 + 1×(x -6)
即 y = x -2.4
(2)当x=8时,y = 8 - 2.4 = 5.6
故,该用户5月份的水费为5.6元.
(3)数学与生活、生产实际有密切联系,我们碰到实际问题要善于用数学方法去分析、去解决,看到数学的函数图像也要善于给它赋予不同的意义,这是学好数学的秘诀之一。
(1)识别、分析函数图像所描述的信息;
2.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药(1)服药后____时,血液中含药量最高,达到每毫升_______毫克。(2)服药5时,血液中含药量为每毫升____毫克。(3)当x≤2时,y与x之间的函数关系式是_____。(4)当x≥2时,y与x之间的函数关系式是_________。(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是___ 小时。.
点评(1)根据图像反映的信息解答有关问题时,首先要弄清楚两坐标轴的实际意义,抓住几个关键点来解决问题;(2)特别注意,第5问中由y=3对应的x值有两个;(3)根据函数图像反映的信息来解答有关问题,比较形象、直观,从中能进一步感受“数形结合思想”。
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药的一定时间内每毫升血液中含药量y(微克)随时间x(时)逐步增加,变化情况如图所示.
(1)当0≤ x≤2时,y与x之间的函数关系式是 。













