初中第二十七章 相似综合与测试精品单元测试课时练习

这是一份初中第二十七章 相似综合与测试精品单元测试课时练习，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

第27章相似单元测试题
考试时间：90分钟；总分：120分
一、单选题(将唯一正确答案的代号填在题后的括号内，每题3分，共30分)
1．下列说法正确的是（ ）
A．边数相同的两个正多边形相似
B．边数相同且对应角相等的两个多边形相似
C．边数相同且对应边成比例的两个多边形相似
D．边数相同、周长相等且对应角相等的两个多边形相似
2．在直角三角形ABC中，CD是斜边上的高线，则下列各式能成立的是(　　)
A． B． C． D．

2题图 3题图 4题图
3．如图，点、分别在的、边上，增加下列哪些条件：①；②；③，使与一定相似（ ）
A．①③ B．②③ C．①② D．①②③
4．如图，AB∥CD，AB＝6，CD＝9，AD＝10，则OD的长为（　　）
A．4 B．5 C．6 D．7
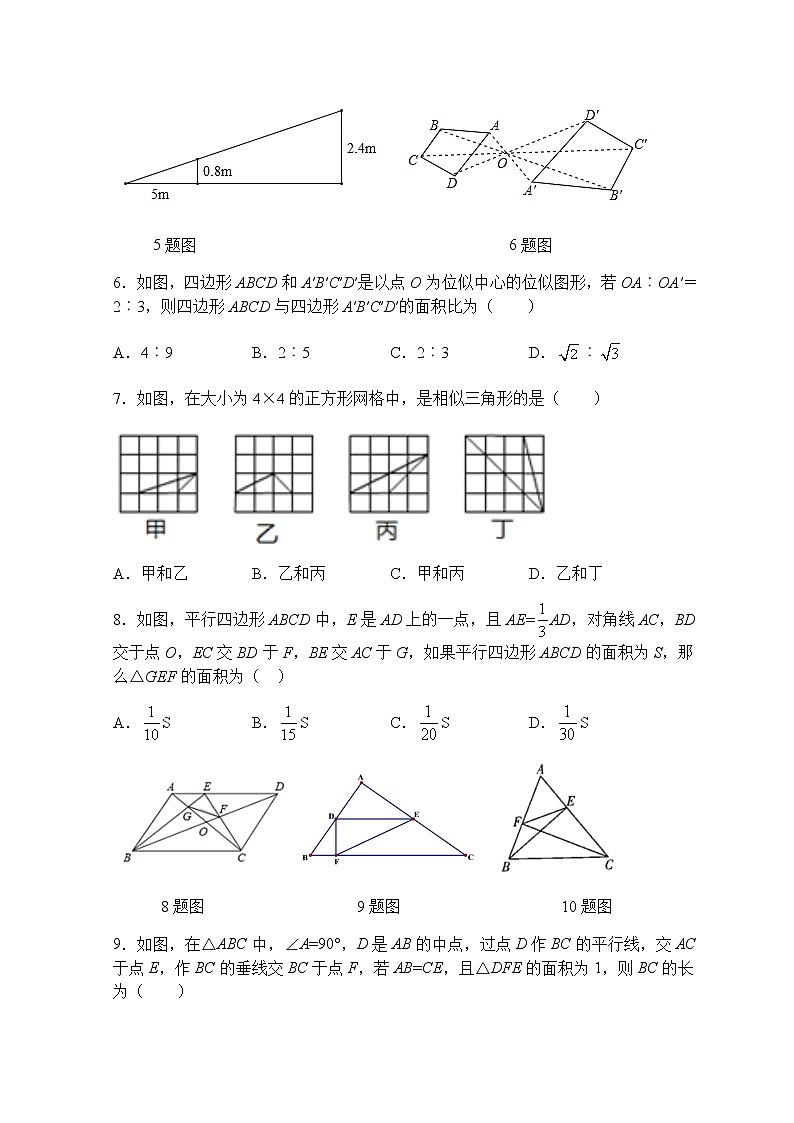
5．小明在打网球时，为使球恰好能过网（网高0.8米），且落在对方区域离网5米的位置上，已知他的击球高度是2.4米，则他应站在离网的（ ）
A．7.5米处 B．8米处 C．10米处 D．15米处

5题图 6题图
6．如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA︰OA′＝2︰3，则四边形ABCD与四边形A′B′C′D′的面积比为（　　）
A．4︰9 B．2︰5 C．2︰3 D．︰
7．如图，在大小为4×4的正方形网格中，是相似三角形的是（ ）

A．甲和乙 B．乙和丙 C．甲和丙 D．乙和丁
8．如图，平行四边形ABCD中，E是AD上的一点，且AE=AD，对角线AC，BD交于点O，EC交BD于F，BE交AC于G，如果平行四边形ABCD的面积为S，那么△GEF的面积为（ ）
A．S B．S C．S D．S

8题图 9题图 10题图
9．如图，在△ABC中，∠A=90°，D是AB的中点，过点D作BC的平行线，交AC于点E，作BC的垂线交BC于点F，若AB=CE，且△DFE的面积为1，则BC的长为（ ）
A． B．5 C． D．10
10．如图，在△ABC中，∠A=60°，BE、CF分别是AC、AB边上的高，连接EF，则EF︰BC的值为( )
A．1︰2 B．2︰3 C．1︰4 D．2︰5
二、填空题(将正确答案填在题中的横线上，每题3分，共24分)
11．如果，那么______．
12．如图，1∥2∥3，，则________________．

12题图 13题图
13．在△ABC中，DE∥BC, ∠ADE=∠EFC,AD∶BD=5∶3，CF=6，则DE的长为__________．
14．如图，在平行四边形ABCD中，点E在BC边上，且CE︰BC＝2︰3，AC与DE相交于点F，若S△EFC=8，则S△CFD＝________．

14题图 15题图 16题图
15．如图所示，点，，在轴上，且，分别过点，，作轴的平行线，与反比例函数的图象分别交于点，，，分别过点，，作轴的平行线，分别于轴交于点，，，连接，，，那么图中阴影部分的面积之和为______________．
16．如图，矩形OABC，点A、C分别在x轴、y轴上，点B坐标为(k, 2k)， 连接OB，将矩形OABC沿OB折叠，点A的对应点为点D，则点D的坐标为 (用含k的式子表示)．
17．如图，有一张直径（BC）为1.2米的圆桌，其高度为0.8米，同时有一盏灯A距地面2米，圆桌的影子是DE，AD和AE是光线，建立图示的平面直角坐标系，其中点D的坐标是（2，0）．那么点E的坐标是____．

17题图 18题图
18．如图所示，正方形OEFG和正方形ABCD是位似图形，点F的坐标为(－1，1)，点C的坐标为(－4，2)，则这两个正方形位似中心的坐标是 ．
三、解答题(本题有8小题，共66分)
19．(本题8分)如图，D、E分别是△ABC的边AB、AC上的点，DE∥BC，AB=7，BD=2，AE=6，求AC的长.

19题图
20．(本题8分)如图，△ABC三个顶点的坐标分别为A（－1，3），B（－1，1），C（－3，2）.
（1）请画出△ABC关于y轴对称的△A1B1C1；
（2）以原点O为位似中心，将△A1B1C1放大为原来的2倍，得到△A2B2C2，
求出△A1B1C1与△A2B2C2的面积.

20题图

21．(本题8分)如图，直线EF分别交△ABC的边AB，AC于点F，E，交BC的延长线于点D，已知BF⋅BA=BC⋅BD.求证：AE⋅CE=DE⋅EF.

21题图


22．(本题8分)如图，在△ABC中，点D，E分别在边AB、AC上，DC与BE相交于点O，且DO＝2，BO＝DC＝6，OE＝3．
（1）求证：DE∥BC；
（2）如果四边形BCED的面积比△ADE的面积大12，求△ABC的面积．

22题图




23．(本题8分)已知：如图所示，在正方形ABCD中，F为DC的中点，E为BC上一点，且EC=BC．求证：AF⊥EF．

23题图





24．(本题8分)感知：如图①，∠C=∠ABD=∠E=90°，可知△ACB∽△BED．（不要求证明）

拓展：如图②，∠C=∠ABD=∠E．求证：△ACB∽△BED．
应用：如图③，∠C=∠ABD=∠E=60°，AC=4，BC=1，则△ABD与△BDE的面积比为　 　．

25．(本题8分)已知：⊙O中两条弦AC，BD交于点E．

（1）如图1，求证：．
（2）如图2，若点B是中点，AD是⊙O直径，AD=10，CD=6．
①求BC的长．
②求．



26．(本题10分)如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．
（1）若△BPQ与△ABC相似，求t的值；
（2）连接AQ、CP，若AQ⊥CP，求t的值．

26题图



第27章相似单元测试题参考答案
1．A. 解析：A.边数相同的两个正多边形对应角相等，对应边成比例，相似，
故A项正确；
B.矩形和正方形的边数相同且对应角相等，但矩形和正方形不相似，故B项错误；
C.菱形和正方形边数相同且对应边成比例，但菱形和正方形不相似，故C项错误；
D.由周长相等的矩形和正方形不相似，易知D项错误.
故选A.
2．D. 解析：根据三角形的面积计算公式可得：AC·BC=AB·CD，
即，故选D．
3．A. 解析： ①∵ ,, 故正确；
②虽然有对应边成比例，但是夹角并不一定相等，所以与不一定相似，故错误；
③∵，，,故正确；
所以正确的是：①③， 故选：A．
4．C. 解析：解：∵AB∥CD，∴△AOB∽△DOC，∴，
∵AB＝6，CD＝9，AD＝10，∴，∴OD＝6，故选C．
5．C. 解析：设他应站在离网的x米处，根据题意得：，解得：x=10．
故选C．
6．A. 解析：∵四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，
OA︰OA′＝2︰3，∴DA︰D′A′＝OA︰OA′＝2︰3，
∴四边形ABCD与四边形A′B′C′D′的面积比为：4︰9，故选：A．
7．C. 解析：∵甲中的三角形的三边分别是：，2，；
乙中的三角形的三边分别是：，，；
丙中的三角形的三边分别是：，，；
丁中的三角形的三边分别是：，，；
只有甲与丙中的三角形的三边成比例：，
∴甲与丙相似．故选：C．
8．C. 解析：过A作AM⊥BC于M，如图所示：
∵S△BEC= BC•AM，S▱ABCD=BC•AM，∴S△BEC=S▱ABCD=S，
∵四边形ABCD是平行四边形， ∴AD∥BC，AD=BC，
∴∠EAG=∠BCG，∠AEG=∠CBG， ∴△AEG∽△CBG，
又AE=AD=BC，∴ ==，
∴S△EFG=S△BGF， 又S△EFG+S△BGF=S△BEF，∴S△EFG=S△BEF，
∵AE=AD，AD=AE+ED， ∴ED=AD=BC，
同理得到△EFD∽△CFB， ∴== ∴S△BEF=S△BFC，
又S△BEF+S△BFC=S△BEC，
∴S△BEF=S△BEC=S， ∴S△EFG=S．故选：C．

9．A. 解析：是AB的中点，
是△ABC的中位线，





故选A．
10．A. 解析：∵BE，CF分别是AC，AB边上的高，∴，
∵，∴，
，即.
又∵，∴，∴.
∵在中，，
∴，.故选项A正确.
11．. 解析：由，可得：，，
所以，故答案为：．
12．4. 解析：∵1∥2∥3，∴，即，∴DE=4．故答案为：4．
13．10. 解析：∵DE∥BC，∴∠AED=∠C，AD∶BD=AE∶EC=5∶3，
又∵∠ADE=∠EFC，∴△ADE∽△EFC，
∴DE∶FC=AE∶EC=5∶3，又∵CF=6，∴DE=10.故答案为：10.
14．12. 解析：∵四边形ABCD是平行四边形，∴BC∥AD、BC=AD，
而CE∶BC=2∶3，∴△AFD∽△CFE，且它们的相似比为3∶2，
∴FD∶FE=3∶2，∴S△CDF∶S△EFC=3∶2，而S△EFC=8，∴S△DFC=12．故答案为：12．
15．. 解析：根据题意可知

∵轴，∴
设图中阴影部分的面积从左向右依次为
则，∴
同理
∴图中阴影部分的面积分别是
∴图中阴影部分的面积之和=．
故答案为：．
16．. 解析：如图，过点D做DE⊥x轴，垂足为E，交BC延长线于点F．
∵矩形OABC中，点B坐标为，∴OA=k，AB=2k．
∵矩形OABC沿OB折叠，∴△OBD≌△OBA，
∴OD= OA=k，BD=BA=2k，∠ODB=∠OAB=90°，
∴∠FDB+∠EDO=90°．
∵∠EOD+∠EDO=90°，∴∠EOD=∠FDB．
∵∠F=∠DEO=90°，∴△OED∽△DFB，
∴．
设DE=m，则BF=2m,OE=2m-k,∴2k-m=2（2m-k）
∴，∴，∴点D坐标为：．

故答案为：．
17．（4，0）. 解析：如图，延长CB交y轴于F，
∵桌面与x轴平行即BF∥OD，∴△AFB∽△AOD，
∵OF=0.8，∴AF=AO-OF=2-0.8=1.2，
∵OA=OD=2，则AF=FB=1.2，BC =1.2，FC=FB+BC=1.2+1.2=2.4，
∵FC∥x轴，∴△AFC∽△AOE，
∴，∴=4，E（4，0）．
故答案为：（4，0）．
．
18．（2，0）或（-，）. 解析：
①当两个位似图形在位似中心同旁时，位似中心就是CF与x轴的交点，
设直线CF解析式为y=kx+b，将C（-4，2），F（-1，1）代入，
得，解得即y=-x+，
令y=0得x=2，∴O′坐标是（2，0）；
②当位似中心O′在两个正方形之间时，
可求直线OC解析式为y=-x，直线DE解析式为y=x+1，
联立，解得，即O′（-，）．
故答案为：（2，0）或（-，）．
19．解：∵AB=7，BD=2，∴AD=AB-BD=5.
∵，∴.
∵AE=6，∴. ∴.
20．解：(1)图略；
(2)由题图得S△A1B1C1＝×2×2＝2.∵将△A1B1C1放大为原来的2倍，得到△A2B2C2，∴△A1B1C1∽△A2B2C2，∴＝，∴＝＝，
∴S△A2B2C2＝4S△A1B1C1＝4×2＝8.
即S△A1B1C1＝2，S△A2B2C2＝8.
21．证明：∵BF⋅BA=BC⋅BD，∴ABBD=BCBF，
又∵∠ABC=∠DBF，∴△ABC∽△DBF，
∴∠A=∠D.又∵∠AEF=∠DEC，
∴△AEF∽△DEC，
∴AEDE=EFEC，即AE⋅CE=DE⋅EF.
22．解：（1）∵OD＝2，DC＝6，OE＝3，
∴OC＝4，＝，＝，∴＝，
∵∠DOE＝∠BOC，∴△DOE∽△COB，
∴∠ODE＝∠OCB，∴DE∥BC．
（2）∵DE∥BC，∴△ADE∽△ABC，
∴＝＝，∴＝，
设△ADE的面积为x，则△ABC的面积为4x，
∴四边形BCED的面积为3x，
由题意3x﹣x＝2x＝12，∴x＝6，∴S△ABC＝4x＝24．
23．证明：∵四边形ABCD是正方形，∴∠C＝∠D＝90°，
∵F是CD中点，∴DF＝CF＝12CD＝12AD，
∵CE＝14BC＝14CD，∴CE：DF＝CF：AD＝1：2，
∴Rt△CEF∽Rt△DFA，∴∠FAD＝∠EFC，
∵∠FAD＋∠DFA＝90°，∴∠EFC＋∠DFA＝90°，
∴∠EFA＝90°，∴AF⊥EF；
24．拓展：证明：∵∠ABE=∠C+∠CAB，∠ABE=∠ABD+∠DBE，∠C=∠ABD，
∴∠CAB=∠DBE，∵∠C=∠E，∴△ACB∽△BED；
应用：解：∵∠ABE=∠C+∠CAB，∠ABE=∠ABD+∠DBE，∠C=∠ABD，
∴∠CAB=∠DBE，∵∠C=∠E=60°，∴△ACB∽△BED，△ACE是等边三角形，
∴AE=AC=4，∴BE=CE﹣BC=3，
∴△ACB与△BED的相似比为：4：3，
∴S△ABC：S△BED=16：9，S△ABC：S△ABE=1：3=16：48，
设S△ABC=16x，则S△ABE=48x，S△BDE=9x
∴S△ABD=S△ABE﹣S△BED=48x﹣9x=39x，
∴S△ABD：S△BDE=39：9=13：3．
故答案为13：3．
25．解：（1）连结AB、CD，

则，
又∵，∴，
∴，即．
（2）①连结OB交AC于点M，

∵点B是弧AC的中点，OB为⊙O的半径，
∴，，
∵是⊙的直径，∴，
∴．
∴，
在中，由勾股定理得：
，
∴，
∴在中，
．
②．
26. 解：根据勾股定理得：BA=62+82=10；
（1）分两种情况讨论：
①当△BPQ∽△BAC时，BPBA=BQBC，
∵BP＝5t，QC＝4t，AB＝10，BC＝8，
∴5t10=8-4t8，解得，t＝1，
②当△BPQ∽△BCA时，BPBC=BQBA，
∴5t8=8-4t10，解得，t=3241；
∴t＝1或3241时，△BPQ∽△BCA；
（2）过P作PM⊥BC于点M，AQ，CP交于点N，如图所示：
则PB＝5t，PM＝3t，MC＝8﹣4t，
∵∠NAC+∠NCA＝90°，∠PCM+∠NCA＝90°，
∴∠NAC＝∠PCM，
∵∠ACQ＝∠PMC，∴△ACQ∽△CMP，
∴ACCM=CQMP，∴68-4t=4t3t，解得t=78．

26题图