人教版九年级下册27.2.1 相似三角形的判定评优课课件ppt

这是一份人教版九年级下册27.2.1 相似三角形的判定评优课课件ppt，文件包含2721第2课时三边成比例的两个三角形相似ppt、2721第2课时三边成比例的两个三角形相似导学案doc等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
1. 复习已经学过的三角形相似的判定定理.2. 掌握利用三边来判定两个三角形相似的方法，并能进 行相关计算. (重点、难点)
2. 证明三角形全等有哪些方法？你能从中获 得证明三角形相似的启发吗？
1. 什么是相似三角形？在前面的课程中，我们学过哪 些判定三角形相似的方法？你认为这些方法是否有 其缺点和局限性？
3. 类似于判定三角形全等的 SSS 方法，我们能不能通 过三边来判定两个三角形相似呢？
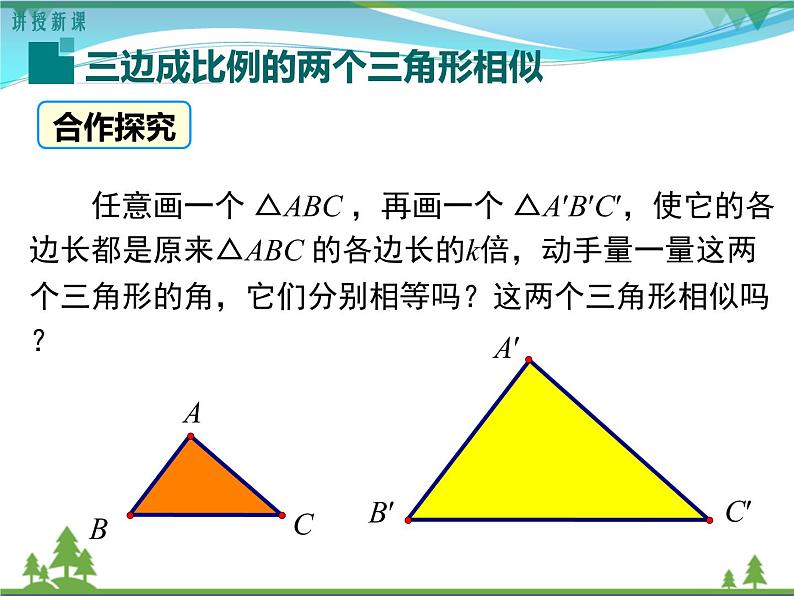
任意画一个 △ABC ，再画一个 △A′B′C′，使它的各边长都是原来△ABC 的各边长的k倍，动手量一量这两个三角形的角，它们分别相等吗？这两个三角形相似吗？
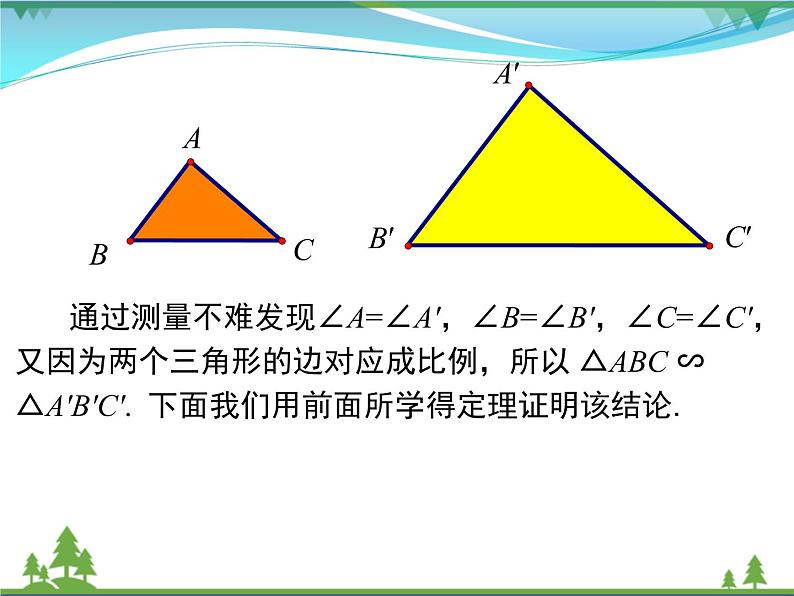
通过测量不难发现∠A=∠A'，∠B=∠B'，∠C=∠C'，又因为两个三角形的边对应成比例，所以 △ABC ∽△A′B′C′. 下面我们用前面所学得定理证明该结论.
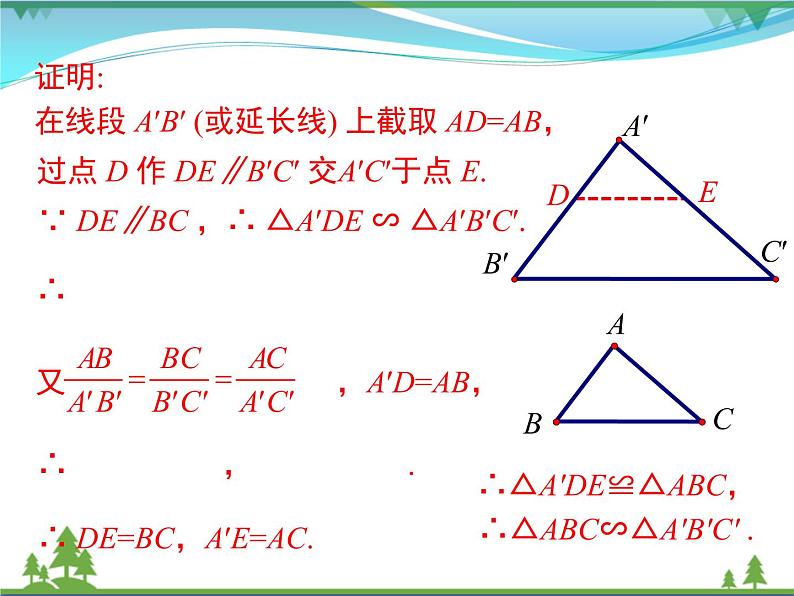
证明:在线段 A′B′ (或延长线) 上截取 AD=AB，
过点 D 作 DE∥B′C′ 交A′C′于点 E.
∵ DE∥BC ，∴ △A′DE ∽ △A′B′C′.
∴ DE=BC，A′E=AC.
∴△A′DE≌△ABC， ∴△ABC∽△A′B′C′ .
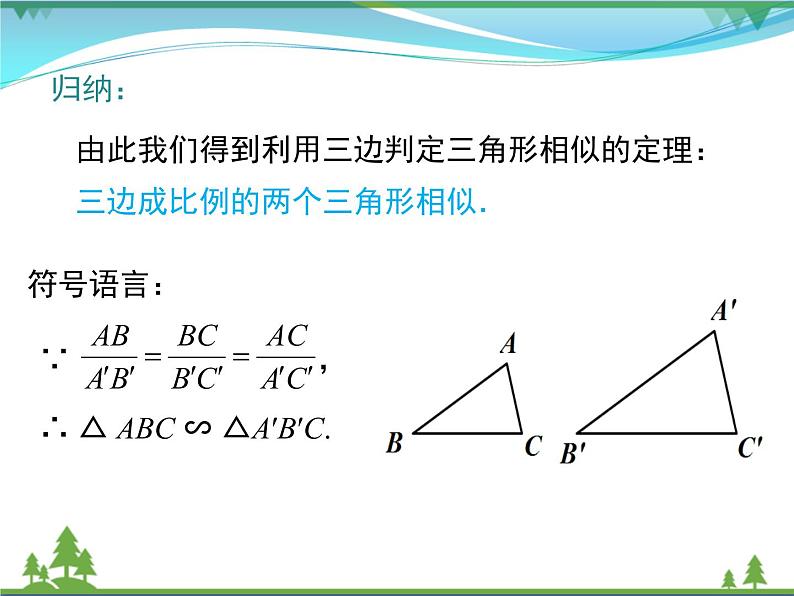
由此我们得到利用三边判定三角形相似的定理：三边成比例的两个三角形相似．
∴ △ ABC ∽ △A′B′C.
例1 根据下列条件，判断△ABC与△A′B′C′是否相似，并说明理由.
AB=4 cm ，BC =6 cm ，AC =8 cm，A′B′=12 cm ，B′C′=18 cm ，A′C′=24 cm.
解：相似.理由如下：∵ ∴∴△ABC∽△A′B′C′.
已知 △ABC 和 △DEF，根据下列条件判断它们是否相似.
(2) AB=4， BC =8， AC＝10， DE＝20，EF＝16， DF＝8.
(1) AB =3， BC =4， AC＝6， DE＝6， EF＝8， DF＝9；
例2 判断图中的两个三角形是否相似，并说明理由．
解：在 △ABC 中，AB > BC > CA，在 △ DEF中， DE > EF > FD.
∴ △ABC ∽ △DEF.
方法总结：判定三角形相似的方法之一：如果题中给出了两个三角形的三边的长，分别算出三条对应边的比值，看是否相等.注意：计算时最长边与最长边对应，最短边与最短边对应.
【分析】要运用三边成比例判断相似，目前题目只有2组边成比例和90°的角，那么可以通过“勾股定理”得到第三组边成比例，进而求解.
证明：由已知条件得 AB = 2 A′B′，AC = 2 A′C′，
∴ BC 2 = AB 2－AC 2 = ( 2 A′B′ )2－( 2 A′C′ )2 = 4 A′B′ 2－ 4 A′C′ 2 = 4 ( A′B′ 2－A′C′ 2 ) = 4 B′C′ 2 = ( 2 B′C′ )2.
∴ △ A′B′C′∽△ABC.
∴∠BAC=∠DAE，∠BAC －∠DAC = ∠DAE －∠DAC，即 ∠BAD=∠CAE.∵∠BAD=20°，∴∠CAE=20°.
∴ △ABC ∽△ADE (三边成 比例的两个三角形相似).
例4 如图，在 △ABC 和 △ADE 中， ∠BAD=20°，求∠CAE的度数.
1. 根据下列条件，判断△ABC与△A′B′C′是否相似，并说明理由
AB=5 cm ，BC =7 cm ，AC =8 cm，A′B′=15 cm ，B′C′=21 cm ，A′C′=23 cm.
解：不相似.理由如下：∵ ，∴△ABC与△A′B′C′的三边不成比例，∴不相似.
2. 如图，在大小为4×4的正方形网格中，有两个三角形，它们是否相似？请说明理由.
解：相似，图①中的三角形三边分别为 ，2 ， ；图②中的三角形三边分别为 2，2 ，2 .则 ，所以这两个三角形相似.
3. 如图，∠APD=90°，AP=PB=BC=CD=1，求证： △ABC∽△DBA.
∵ AB : BC = BD : AB = AD : AC，∴△ABC∽△DBA.
证明：∵∠APD=90°，AP=PB=BC=CD=1，∴AB= ，AC= ，AD= .
4. 如图，△ABC中，点 D，E，F 分别是 AB，BC，CA 的中点，求证：△ABC∽△EFD．
∴ △ABC∽△EFD.
证明：∵△ABC中，点D，E，F分别是AB，BC，CA的中点，
5. 如图，某地四个乡镇 A，B，C，D 之间建有公路， 已知 AB = 14 千米，AD = 28 千米，BD = 21 千米， DC = 31.5 千米，公路 AB 与 CD 平行吗？说出你 的理由.
解：公路 AB 与 CD 平行.
∴ △ABD∽△BDC，∴∠ABD=∠BDC，∴AB∥DC.