

- 苏教版数学六年级下学期期末测试卷2(含答案) 试卷 2 次下载
- 苏教版数学六年级下学期期末测试卷3(含答案) 试卷 2 次下载
- 苏教版数学六年级下学期期末测试卷5(含答案) 试卷 1 次下载
- 苏教版数学六年级下学期期末测试卷6(含答案) 试卷 1 次下载
- 苏教版数学六年级下学期期末测试卷7(含答案) 试卷 1 次下载
苏教版数学六年级下学期期末测试卷4(含答案)
展开苏教版数学六年级下学期期末测试卷
一、用心思考,认真填写(每小题2分,计22分)
1.我国香港特别行政区的总面积是十一亿零三百万平方米,写作 平方米,改写成用“亿”作单位的数是 平方米.
2.0.6公顷= 平方米; 1小时15分= 小时.
3. :20=0.6=15÷ = %= (折数)
4.m=n+1(m、n为非零0自然数),m和n的最大公因数是 ,m和n的最小公倍数是 .
5.如果小明向南走80米,记作+80米,那么小华从同一地点向北走50米,记作 米,这时他们两人相距 米.
6.线段比例尺改写成数字比例尺是 ,在这幅图上量得北京到上海的距离是5厘米,北京到上海的实际距离是 千米.
7.一个平行四边形的两条邻边的长度分别是6厘米、8厘米,其中一条底上的高是7厘米,这个平行四边形的周长是 厘米,面积是 平方厘米.
8.一根圆柱形的木料长4米,把它锯成3段,表面积增加了12平方分米,这根木料的体积是 立方分米.如果锯成3段用了3分钟,那么把它锯成6段要用 分钟.
9.一个长方形的面积是72平方厘米,长和宽的比是2:1,这个长方形的周长是 厘米.
10.仔细观察如表中两种量x和y的变化情况.用一个含x、y的式子表示它们之间的关系是 ,x和y是成 比例关系的量.
x
6
12
18
24
…
y
30
15
10
7.5
…
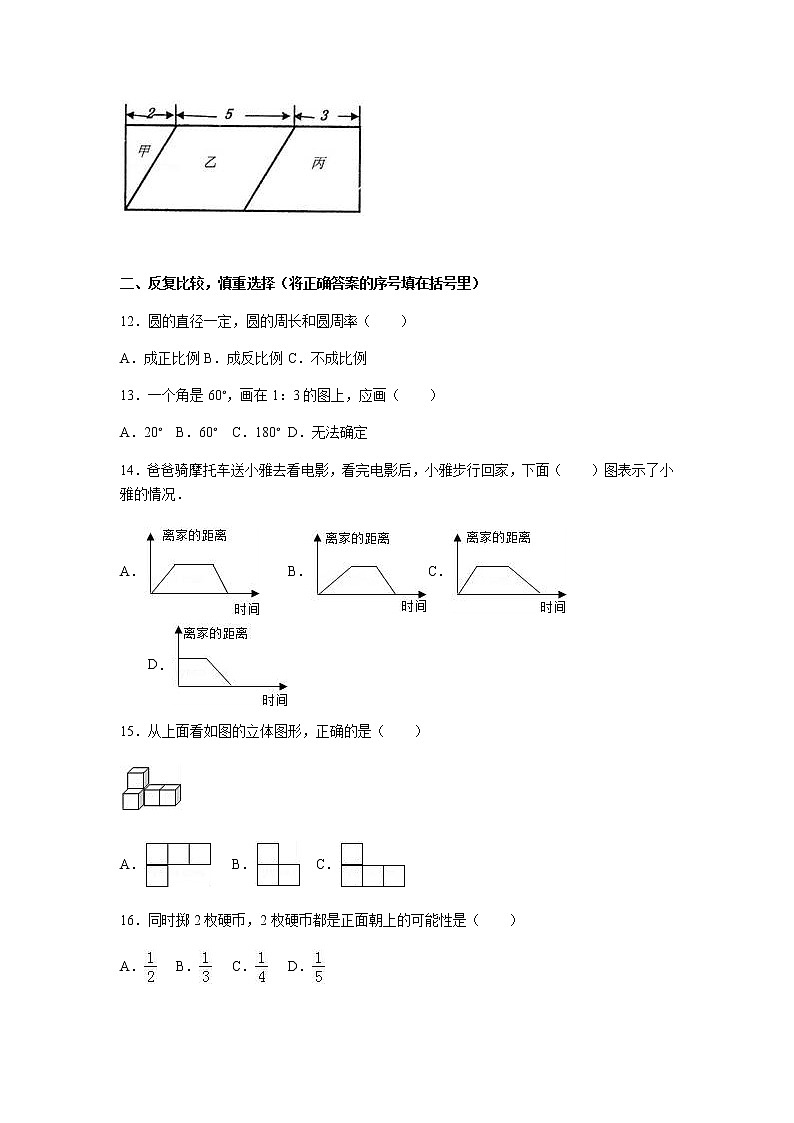
11.如图,甲、乙、丙三个图形面积的比是 .
二、反复比较,慎重选择(将正确答案的序号填在括号里)
12.圆的直径一定,圆的周长和圆周率( )
A.成正比例 B.成反比例 C.不成比例
13.一个角是60°,画在1:3的图上,应画( )
A.20° B.60° C.180° D.无法确定
14.爸爸骑摩托车送小雅去看电影,看完电影后,小雅步行回家,下面( )图表示了小雅的情况.
A. B. C. D.
15.从上面看如图的立体图形,正确的是( )
A. B. C.
16.同时掷2枚硬币,2枚硬币都是正面朝上的可能性是( )
A. B. C. D.
三、仔细推敲,认真辨析
17.某车间今年比去年产量增加了25%,则去年就比今年产量减少了20%. (判断对错).
18.2100年全年有365天. .
19.要反映某厂今年前五个月产值增减变化情况,适合选择条形统计图. (判断对错).
20.把3个饼干平均分给4个小朋友,每人分得一个饼的. .
21.某种奖券的中奖率为1%,买100张不一定能中奖. (判断对错).
四、认真审题,细心计算(8+12+9=29分)
22.直接写出计算结果.
6.7+4.3=
0.32=
12=
3%×5%=
8÷0.02=
﹣=
=
3a×4a=
23.计算下面各题,能简便的用简便方法计算.
560÷16÷5
6﹣÷6
11×()×7
[﹣()]×.
24.求下面未知数x的值
50%x﹣0.2x=15; x=12; 6:30=x:0.5.
五、观察思考,动手操作(3+4+4=11分)
25.(1)如图中长方形的A点在( , )处.
(2)将原来的长方形绕C点顺时针旋转90°,画出旋转后的图形.
(3)将原来的长方形按1:2缩小,并将缩小后的图形画在方格内.
26.右边是跳伞运动员一次训练中落地位置示意图.
①1号运动员的落地点在靶心的 偏 度方向 米处.
②2号运动员的落地点在靶心的北偏东70°方向15米处.在图中表示出2号运动员的落地位置.
27.探索规律.
正方体个数
1
2
3
4
5
6
…
N
…
正方形个数
6
10
14
18
…
62
…
六、灵活运用,解决问题(8+20=28分)
28.只列式,不计算.
(1)小李存了20000元三年定期储蓄,年利率是4.25%,到期时应得利息多少元?
(2)电冰箱厂五月计划生产5000台电冰箱,实际比计划多生产了400台,超产了百分之几?
(3)一辆汽车从甲地开往乙地,行了全程的,两地相距240千米,这是汽车离甲地多少千米?
(4)某养殖厂养鸡300只,养鸡的只数和鸭的只数比是2:3.养殖厂养鸭多少只?
29.修路队修一条长600米的路,第一天修了全长的20%,第二天再修多少米就正好修完全长的一半?
30.甲乙两车同时从相距120千米的A、B两地相对开出,小时相遇,甲车每小时行100千米,乙车每小时行多少千米?
31.一个圆锥形小麦堆,把这堆小麦装进圆柱形粮屯正好装满,粮屯的底面直径是4米,高3米,这个圆锥形小麦堆的体积是多少立方米?
32.银桥小学有3个同样大的花圃和3个同样大的苗铺,一共是180平方米,每个花圃比苗圃小10平方米,每个花圃和苗圃的面积分别是多少平方米?
33.一种足球,甲、乙、丙三家商店的价格都是每个25元,学校要买60个,三个商店促销方式如下:甲商店是买10个送2个,不足10个不送;乙商店可以打八五折;丙商店是购物每满100元,返还20元.学校到哪家商店购买比较合算?最少需要多少元?
参考答案与试题解析
一、用心思考,认真填写(每小题2分,计22分)
1.我国香港特别行政区的总面积是十一亿零三百万平方米,写作 1103000000 平方米,改写成用“亿”作单位的数是 11.03亿 平方米.
【考点】整数的读法和写法;整数的改写和近似数.
【分析】(1)整数的写法:整数的写法是从高位写起,一级一级地往下写,哪个数位上有几个单位就在那个数位上写几,一个单位也没有时用“0”来占位;
(2)把一个数改写成用“亿”作单位的数,从个位数到亿位,在亿位的右下角点上小数点,末尾的零去掉,再添上一个“亿”字.
【解答】解:(1)十一亿零三百万:在十亿位上写1,在亿位数上写1,在百万位数上写3,剩下的数位上都写0,故写作:1103000000;
(2)1103000000=11.03亿.
故答案为:1103000000,11.03亿.
2.0.6公顷= 6000 平方米; 1小时15分= 1.25 小时.
【考点】面积单位间的进率及单位换算;时、分、秒及其关系、单位换算与计算.
【分析】(1)高级单位公顷化低级单位平方米乘进率10000.
(2)把15分除以进率60化成0.25小时再与1小时相加.
【解答】解:(1)0.6公顷=6000平方米;
(2)1小时15分=1.25小时.
故答案为:6000,1.25.
3. 12 :20=0.6=15÷ 25 = 60 %= 六 (折数)
【考点】比与分数、除法的关系.
【分析】把0.6化成分数并化简是,根据比与分数的关系=3:5,再根据比的基本性质比的前、后项都乘4就是12:20;根据分数与除法的关系=3÷5,再根据商不变的性质被除数、除数都乘5就是15÷25;把0.6的小数点向右移动两位添上百分号就是60%;根据折扣的意义60%就是六折.
【解答】解:12:20=0.6=15÷25=60%=六折.
故答案为:12,25,60,六.
4.m=n+1(m、n为非零0自然数),m和n的最大公因数是 1 ,m和n的最小公倍数是 mn .
【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【分析】如果a+1=b(a和b都是不为0的自然数),则说明这两个数是相邻的自然数,如5、6,那么这两个数互质,那么a和b的最大公因数是 1,最小公倍数是它们的积;据此解答.
【解答】解:如果m=n+1(m、n为非零0自然数),m和n互质,
所以m和n的最大公因数是 1,最小公倍数是mn.
故答案为:1,mn.
5.如果小明向南走80米,记作+80米,那么小华从同一地点向北走50米,记作 ﹣50 米,这时他们两人相距 130 米.
【考点】负数的意义及其应用.
【分析】此题主要用正负数来表示具有意义相反的两种量:向南走记为正,则向北走就记为负,直接得出结论即可.
【解答】解:如果小明向南走80米,记作+80米,那么小华从同一地点向北走50米,记作﹣50米,这时他们两人相距80+50=130米;
故答案为:﹣50,130.
6.线段比例尺改写成数字比例尺是 1:25000000 ,在这幅图上量得北京到上海的距离是5厘米,北京到上海的实际距离是 1250 千米.
【考点】比例尺.
【分析】根据比例尺的意义可把线段比例尺改写成数字比例尺,求北京到上海的实际距离,根据公式“图上距离÷比例尺=实际距离”,代入数字,进行列式解答,即可得出结论.
【解答】解:250千米=25000000厘米
比例尺为:1:25000000
5÷=125000000(厘米)
125000000厘米=1250(千米)
答:改写成数字比例尺是1:25000000,北京到上海的实际距离是1250千米.
故答案为:1:25000000,1250.
7.一个平行四边形的两条邻边的长度分别是6厘米、8厘米,其中一条底上的高是7厘米,这个平行四边形的周长是 28 厘米,面积是 42 平方厘米.
【考点】平行四边形的面积.
【分析】依据在直角三角形中斜边最长,先判断出7厘米高的对应底边是6厘米,进而利用平行四边形的周长公式和面积公式解答即可.
【解答】解:(6+8)×2
=14×2
=28(厘米)
6×7=42(平方厘米)
答:这个平行四边形的周长是 28厘米,面积是 42平方厘米.
故答案为:28;42.
8.一根圆柱形的木料长4米,把它锯成3段,表面积增加了12平方分米,这根木料的体积是 120 立方分米.如果锯成3段用了3分钟,那么把它锯成6段要用 7.5 分钟.
【考点】简单的立方体切拼问题;圆柱的侧面积、表面积和体积.
【分析】(1)锯成3段,就增加了12平方分米,也就是增加了2×2=4个圆柱的底面积,由此可以求得这个圆柱的底面积解决问题;
(2)锯成3段,实际锯了3﹣1=2次,由此可以求得锯一次用时:3÷2=1.5分钟,则锯成6段需要锯6﹣1=5次,由此即可解决问题.
【解答】解:(1)长4米=40分米,
12÷(2×2)×40,
=12÷4×40,
=120(立方分米);
(2)3÷(3﹣1)×(6﹣1),
=3÷2×5,
=1.5×5,
=7.5(分钟);
答:这根木料的体积是120立方分米.如果锯成3段用了3分钟,那么把它锯成6段要用7.5分钟.
故答案为:120;7.5.
9.一个长方形的面积是72平方厘米,长和宽的比是2:1,这个长方形的周长是 36 厘米.
【考点】长方形的周长;长方形、正方形的面积.
【分析】设宽为x厘米,那么长为2x厘米,根据面积是72平方厘米可得:2x×x=72,解得x=6,则长为2×6=12厘米,然后长方形周长=(长+宽)×2解答即可.
【解答】解:设宽为x厘米,那么长为2x厘米,
2x×x=72
x2=36
x=6
2×6=12(厘米)
(12+6)×2
=18×2
=36(厘米)
答:这个长方形的周长是 36厘米.
故答案为:36.
10.仔细观察如表中两种量x和y的变化情况.用一个含x、y的式子表示它们之间的关系是 xy=k(一定) ,x和y是成 反 比例关系的量.
x
6
12
18
24
…
y
30
15
10
7.5
…
【考点】辨识成正比例的量与成反比例的量.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为:6×30=12×15=18×10=24×7.5=180,是乘积一定,用含x、y的式子表示它们之间的关系是 xy=k(一定),x和y是成反比例;
故答案为:xy=k(一定),反.
11.如图,甲、乙、丙三个图形面积的比是 1:5:4 .
【考点】比的意义.
【分析】三个图形的高相等,依据各自的面积公式即可推出结果.
【解答】解:三角形的面积=2×高÷2=高;
平行四边形的面积=5×高;
梯形的面积=(3+5)×高÷2=4×高;
由此可以得出它们的面积比是1:5:4.
故答案为:1:5:4.
二、反复比较,慎重选择(将正确答案的序号填在括号里)
12.圆的直径一定,圆的周长和圆周率( )
A.成正比例 B.成反比例 C.不成比例
【考点】辨识成正比例的量与成反比例的量.
【分析】判断圆的周长和圆周率之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为圆的周长C=πd,
在此题中圆的直径一定,圆周率也是一定的,
所以周长也是一定的,
即三个量都是一定的,不存在变量问题,
所以圆的周长和圆周率不成比例;
故选:C.
13.一个角是60°,画在1:3的图上,应画( )
A.20° B.60° C.180° D.无法确定
【考点】图形的放大与缩小;角的概念及其分类.
【分析】根据角的大小与两边张口的大小有关,张口越大,角越大;张口越小,角越小,和两边的长短无关,更和图形的放大与缩小无关,据此即可作出选择.
【解答】解:根据分析可得:
一个角是60°,画在1:3的图上,还应当画60°.
故选:B.
14.爸爸骑摩托车送小雅去看电影,看完电影后,小雅步行回家,下面( )图表示了小雅的情况.
A. B. C. D.
【考点】从统计图表中获取信息.
【分析】根据“爸爸骑摩托车送小雅去看电影,看完电影后,小雅步行回家”,可知骑摩托车的速度快,坡度大,位置有变化;步行回家的速度慢,坡度小,位置也有变化;看电影的位置不变.据此进行选择.
【解答】解:爸爸骑摩托车送小雅去看电影,看完电影后,小雅步行回家,
图C表示了小雅的情况;
故选:C.
15.从上面看如图的立体图形,正确的是( )
A. B. C.
【考点】从不同方向观察物体和几何体.
【分析】从上面看到的图形是有两排,里排有三个正方形,外排有一个正方形靠左;从左侧看到的是有两层,下层有两个正方形,上层有一个正方形靠左;从正面看到的图形有两层,下层有3个正方形,上层有1个正方形靠左;据此解答即可.
【解答】解:由分析画出三个方向看到的图形如下:
故选:A.
16.同时掷2枚硬币,2枚硬币都是正面朝上的可能性是( )
A. B. C. D.
【考点】简单事件发生的可能性求解.
【分析】任意抛掷两枚硬币,出现的结果有:正正,正反,反正,反反,然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可.
【解答】解:任意抛掷两枚硬币,出现的结果有:正正,正反,反正,反反,
所以任意抛掷两枚硬币,两枚都是正面朝上的可能性:
1÷4=
故选:C.
三、仔细推敲,认真辨析
17.某车间今年比去年产量增加了25%,则去年就比今年产量减少了20%. √ (判断对错).
【考点】百分数的实际应用.
【分析】根据“今年比去年产量增加了25%”把去年的产量看作单位“1”,即今年是去年的(1+25%);要求去年产量比今年减少百分之几,用去年产量比今年少的产量除以今年的产量即可.
【解答】解:25%÷(1+25%)
=25%÷125%
=20%,
答:去年就比今年产量减少了20%.
故答案为:√.
18.2100年全年有365天. 正确 .
【考点】年、月、日及其关系、单位换算与计算;平年、闰年的判断方法.
【分析】闫年的判断方法是:一般年份的除以4,整百年份、整千整百年份除以400,如果能整除,这一年是闫年.2100是整百年份,要除以400来判断.平年全年有365天,闫年全年有366天.
【解答】解:2100÷400=5…2,
不能整除,
所以2100年不是闫年是平年,全年有365天.
故答案为:正确.
19.要反映某厂今年前五个月产值增减变化情况,适合选择条形统计图. × (判断对错).
【考点】统计图的选择.
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【解答】解:根据统计图的特点可知:要反映某厂今年前五个月产值增减变化情况,适合选择折线统计图.
故答案为:×.
20.把3个饼干平均分给4个小朋友,每人分得一个饼的. 错误 .
【考点】分数的意义、读写及分类.
【分析】把3个饼干平均分给4个小朋友,根据分数的意义可知,即将这3个饼当做单位“1”平均分成4份,则每人分得这3个饼的1÷4=.即3×=个饼,是一个饼的÷1=.
【解答】解:则每人分得这3个饼的:1÷4=.
是一个饼的:3×÷1=.
故答案为:错误.
21.某种奖券的中奖率为1%,买100张不一定能中奖. √ (判断对错).
【考点】简单事件发生的可能性求解.
【分析】一种彩票的中奖率是1%,属于不确定事件,可能中奖,也可能不中奖,买了100张彩票只能说明比买1张的中奖的可能性大.
【解答】解:由分析知:某种奖券的中奖率为1%,买100张不一定能中奖;√
故答案为:√.
四、认真审题,细心计算(8+12+9=29分)
22.直接写出计算结果.
6.7+4.3=
0.32=
12=
3%×5%=
8÷0.02=
﹣=
=
3a×4a=
【考点】小数四则混合运算;分数的四则混合运算.
【分析】根据小数、分数四则运算的法则及混合运算的运算顺序计算即可.
【解答】解:
6.7+4.3=11
0.32=0.09
12=18
3%×5%=0.0015
8÷0.02=400
﹣=
=
3a×4a=12a2
23.计算下面各题,能简便的用简便方法计算.
560÷16÷5
6﹣÷6
11×()×7
[﹣()]×.
【考点】整数四则混合运算;运算定律与简便运算;分数的四则混合运算.
【分析】(1)根据除法的性质简算;
(2)先同时计算两个除法,再算减法;
(3)运用乘法分配律简算;
(4)先算小括号里面的减法,再算中括号里面的减法,最后算括号外的乘法.
【解答】解:(1)560÷16÷5
=560÷(16×5)
=560÷80
=7;
(2)6﹣÷6
=7﹣
=6;
(3)11×()×7
=11××7+×7×11
=14+11
=25;
(4)[﹣()]×
=[﹣]×
=×
=.
24.求下面未知数x的值
50%x﹣0.2x=15; x=12; 6:30=x:0.5.
【考点】方程的解和解方程.
【分析】(1)先化简方程,再根据等式的性质,两边同时除以0.3求解;
(2)根据等式的性质,两边同时乘以,再两边同时除以求解;
(3)根据比例的性质,化成30x=6×0.5,再根据等式的性质,方程两边同时除以30求解.
【解答】解:(1)50%x﹣0.2x=15
0.3x=15
0.3x÷0.3=15÷0.3
x=50;
(2)x=12
x×=12×
x=8
x÷=8÷
x=32;
(3)6:30=x:0.5
30x=6×0.5
30x÷30=3÷30
x=0.1.
五、观察思考,动手操作(3+4+4=11分)
25.(1)如图中长方形的A点在( 2 , 5 )处.
(2)将原来的长方形绕C点顺时针旋转90°,画出旋转后的图形.
(3)将原来的长方形按1:2缩小,并将缩小后的图形画在方格内.
【考点】作旋转一定角度后的图形;图形的放大与缩小;数对与位置.
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出点A的位置.
(2)根据旋转的特征,长方形绕点C顺时针旋转90°后,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形.
(3)根据图形放大与缩小的意义,把这个长方形的各边缩小到原来的,即可得到按1:2缩小后的图形.
【解答】解:(1)如图中长方形的A点在(2,5)处.
(2)将原来的长方形绕C点顺时针旋转90°,画出旋转后的图形(下图红色部分):
(3)将原来的长方形按1:2缩小,并将缩小后的图形画在方格内(下图绿色部分):
26.右边是跳伞运动员一次训练中落地位置示意图.
①1号运动员的落地点在靶心的 西 偏 南30 度方向 10 米处.
②2号运动员的落地点在靶心的北偏东70°方向15米处.在图中表示出2号运动员的落地位置.
【考点】根据方向和距离确定物体的位置.
【分析】(1)以靶心为观测点,1号运动员的落地点在靶心的左下方,所以1号运动员的落地点在靶心的西偏南30度方向;通过测量距离靶心的图上距离是2厘米,根据比例尺即可算出实际距离;
(2)以靶心为观测点,2号运动员的落地点在靶心的右上方,角度是70度,根据比例尺即可算出距离靶心的图上距离.
【解答】解:(1)通过测量距离靶心的图上距离是2厘米,
2÷=2×500=1000(厘米)=10米;
所以:1号运动员的落地点在靶心的西偏南30度方向10米处.
(2)15米=1500厘米,
1500×=3(厘米);
故答案为:西,南30,10.
27.探索规律.
正方体个数
1
2
3
4
5
6
…
N
…
正方形个数
6
10
14
18
…
62
…
【考点】数与形结合的规律.
【分析】通过分析可知:每增加一个正方体,正方形的个数增加4个,10=6+4,14=6+2×4,18=6+3×4,所以N个正方体的正方形的个数是6+(N﹣1)×4,据此解答即可.
【解答】解:根据分析:第五个正方体:6+(5﹣1)×4=22
第六个正方体:6+(6﹣1)×4=26
有62个正方形时:6+(N﹣1)×4=62
4N=62﹣2
N=15
第N个正方体:6+(N﹣1)×4
如图:
探索规律.
正方体个数
1
2
3
4
5
6
…
15
N
…
正方形个数
6
10
14
18
22
26
…
62
6+(N﹣1)×4
…
六、灵活运用,解决问题(8+20=28分)
28.只列式,不计算.
(1)小李存了20000元三年定期储蓄,年利率是4.25%,到期时应得利息多少元?
(2)电冰箱厂五月计划生产5000台电冰箱,实际比计划多生产了400台,超产了百分之几?
(3)一辆汽车从甲地开往乙地,行了全程的,两地相距240千米,这是汽车离甲地多少千米?
(4)某养殖厂养鸡300只,养鸡的只数和鸭的只数比是2:3.养殖厂养鸭多少只?
【考点】百分数的实际应用;简单的行程问题;比的应用.
【分析】(1)根据:利息=本金×年利率×时间,由此代入数据求出利息;注意时间和利率的对应.
(2)用超产的量除以原计划的量,即为超产了百分之几.
(3)行了全程的,两地相距240千米;根据分数乘法的意义,运用乘法求出已行驶的路程,即为汽车离甲地多少千米.
(4)鸡的只数和鸭的只数比是2:3;则鸭的只数是鸡的只数,已知鸡300只,根据分数乘法的意义,运用乘法即可求出鸭的只数.
【解答】解:(1)20000×4.25%×3=2550(元)
答:到期时应得利息2550元.
(2)400÷5000
=0.08
=8%
答:超产了8%.
(3)240×=180(千米)
答:这时汽车离甲地180千米.
(4)300×=450(只)
答:养殖厂养鸭450只.
29.修路队修一条长600米的路,第一天修了全长的20%,第二天再修多少米就正好修完全长的一半?
【考点】百分数的实际应用.
【分析】把全长看作单位“1”,则第二天再修50%﹣20%时正好修完全长的一半,已知全长600米,运用乘法即可求出第二天再修多少米.
【解答】解:600×(50%﹣20%)
=600×30%
=180(米)
答:第二天再修180米就正好修完全长的一半.
30.甲乙两车同时从相距120千米的A、B两地相对开出,小时相遇,甲车每小时行100千米,乙车每小时行多少千米?
【考点】简单的行程问题.
【分析】先根据路程=速度时间,求出甲车小时行驶的路程,再求出乙车行驶的路程,最后根据速度=路程÷时间即可解答.
【解答】解:(120-100×)÷
=×
=80(千米)
答:乙车每小时行80千米.
31.一个圆锥形小麦堆,把这堆小麦装进圆柱形粮屯正好装满,粮屯的底面直径是4米,高3米,这个圆锥形小麦堆的体积是多少立方米?
【考点】关于圆锥的应用题.
【分析】根据题干,此题就是求底面直径为4米,高为3米的圆柱的体积,利用圆柱的体积=底面积×高,代入数据计算即可.
【解答】解:3.14×(4÷2)2×3
=3.14×12
=37.68(立方米),
答:这个圆锥形小麦堆的体积是137.68立方米.
32.银桥小学有3个同样大的花圃和3个同样大的苗铺,一共是180平方米,每个花圃比苗圃小10平方米,每个花圃和苗圃的面积分别是多少平方米?
【考点】和差问题.
【分析】根据题干,每块花圃比每块苗圃大10平方米,那么花圃的总面积比苗圃的总面积就多10×3=30平方米,如果花圃的总面积减去这30平方米,就与苗圃的总面积相等,由此即可求得苗圃的总面积.
【解答】解:苗圃的总面积为:(180-10×3)÷2
=150÷2
=75(平方米)
则花圃的总面积为:180﹣75=105(平方米),
所以每块花圃的面积是105÷3=35(平方米),
每块苗圃的面积是:75÷3=25(平方米),
答:每块花圃面积35平方米,每块苗圃面积25平方米.
33.一种足球,甲、乙、丙三家商店的价格都是每个25元,学校要买60个,三个商店促销方式如下:甲商店是买10个送2个,不足10个不送;乙商店可以打八五折;丙商店是购物每满100元,返还20元.学校到哪家商店购买比较合算?最少需要多少元?
【考点】最优化问题.
【分析】根据题意,分别算出,到甲、乙、丙三个商店买球所花的钱数,看哪家商店需要的钱最少,就到哪家商店购买.
【解答】解:甲:买50个,送50÷10×2=10个球,
50×25=1250(元)
乙:60×25×85%=1275(元)
丙:60×25÷100=15
15×20=300(元)
25×60﹣300=1200(元)
因为1200<1250<1275
所以,学校应该在丙商店购买.
答:学校应该在丙商店购买比较合算,最少需要1200元.
苏教版数学六年级下学期期末测试卷4: 这是一份数学六年级下册本册综合课时训练,共18页。试卷主要包含了用心思考,认真填写,反复比较,慎重选择,仔细推敲,认真辨析,认真审题,细心计算,观察思考,动手操作,灵活运用,解决问题等内容,欢迎下载使用。
苏教版数学六年级下学期期中测试卷4(含答案解析): 这是一份苏教版数学六年级下学期期中测试卷4(含答案解析),共21页。试卷主要包含了填空题,择优选择,我公心!,无误计算,我细心!,实践操作,我精心!,合情推理,我开心!等内容,欢迎下载使用。
苏教版数学六年级下学期期末测试卷7(含答案): 这是一份苏教版数学六年级下学期期末测试卷7(含答案),共21页。试卷主要包含了想想填填.,认真判断.,细心选择.,正确计算.,动手,解决问题.等内容,欢迎下载使用。













