初中人教版18.1.2 平行四边形的判定试讲课ppt课件

这是一份初中人教版18.1.2 平行四边形的判定试讲课ppt课件，共27页。PPT课件主要包含了情景引入，导入新课，讲授新课，你能证明吗，一组对应边相等，两组对边分别相等，证一证，ABCD，ACCA，∠1∠2等内容，欢迎下载使用。
1.掌握“一组对边平行且相等的四边形是平行四边形” 的判定方法.（重点）2.会进行平行四边形的性质与判定的综合运用.（难点）
数学来源于生活，高铁被外媒誉为我国新四大发明之一，我们知道铁路的两条直铺的铁轨互相平行，那么铁路工人是怎样的确保它们平行的呢？
只要使互相平行的夹在铁轨之间的枕木长相等就可以了
那这是为什么呢？会不会跟我们学过的平行四边形有关呢？
问题 我们知道，两组对边分别平行或相等的是平行四边形.如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢？
猜想1：一组对边相等的四边形是平行四边形.
等腰梯形不是平行四边形，因而此猜想错误.
猜想2：一组对边平行的四边形是平行四边形.
梯形的上下底平行，但不是平行四边形，因而此猜想错误.
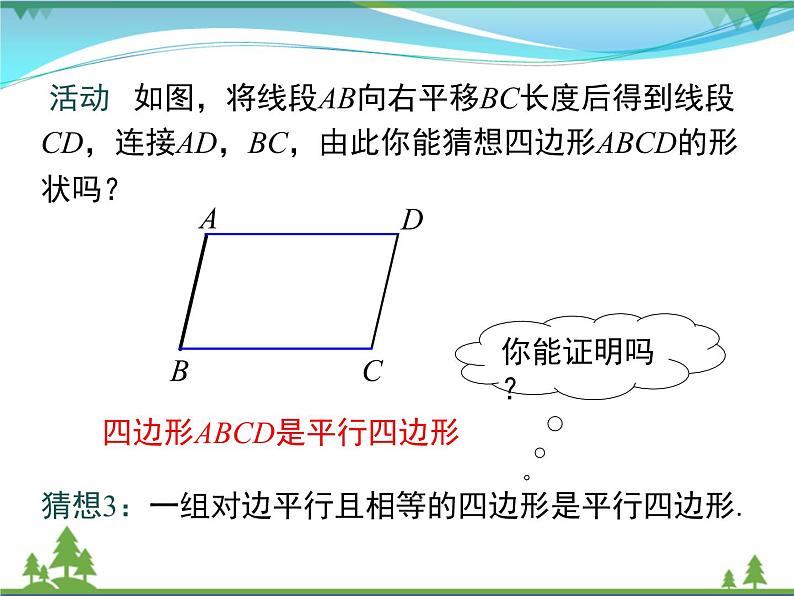
活动 如图，将线段AB向右平移BC长度后得到线段 CD，连接AD，BC，由此你能猜想四边形ABCD的形状吗？
四边形ABCD是平行四边形
猜想3：一组对边平行且相等的四边形是平行四边形.
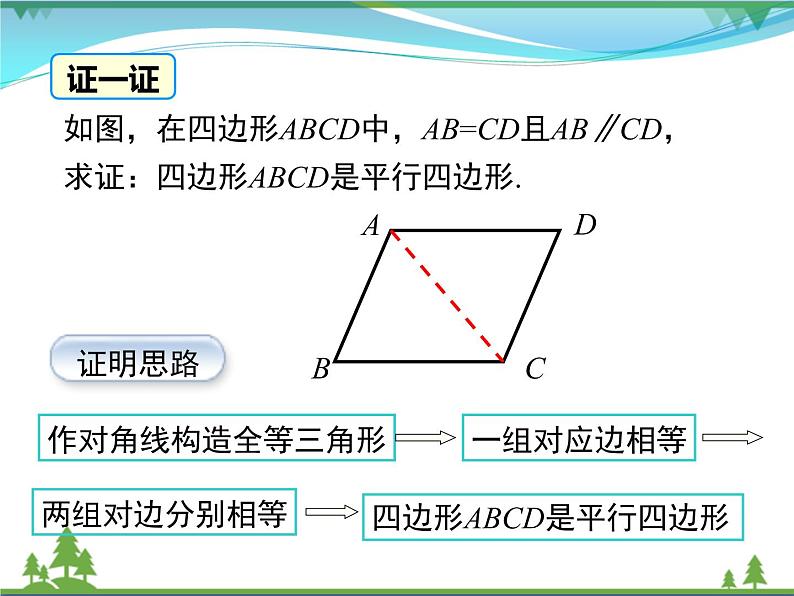
作对角线构造全等三角形
如图，在四边形ABCD中，AB=CD且AB∥CD，求证：四边形ABCD是平行四边形.
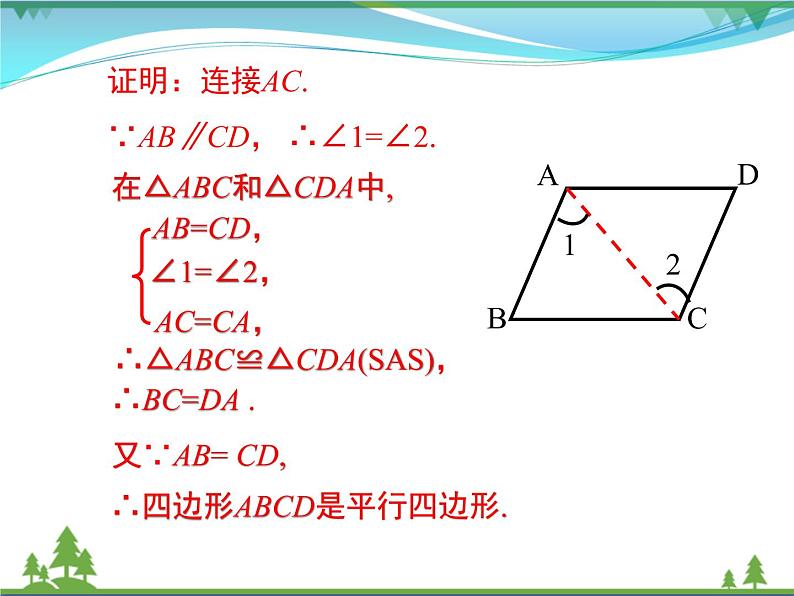
证明：连接AC.∵AB∥CD， ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS)，
∴BC=DA .又∵AB= CD,
∴四边形ABCD是平行四边形.
平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形.
证明： ∵四边形ABCD是平行四边形，∴AB =CD，EB //FD．又∵EB = AB ，FD = CD，∴EB =FD ．∴四边形EBFD是平行四边形．
例1 如图 ，在平行四边形ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形.
例2 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，AE=DF，∠A=∠D，AB=DC．求证：四边形BFCE是平行四边形．
证明：∵AB=CD，∴AB+BC=CD+BC，即AC=BD，在△ACE和△DBF中， AC＝BD ,∠A＝∠D, AE＝DF ,∴△ACE≌△DBF(SAS)，∴CE=BF，∠ACE=∠DBF，∴CE∥BF，∴四边形BFCE是平行四边形．
【变式题】 如图，点C是AB的中点，AD=CE，CD=BE．（1）求证：△ACD≌△CBE；（2）连接DE，求证：四边形CBED是平行四边形．
证明：（1）∵点C是AB的中点，∴AC=BC.在△ADC与△CEB中， AD＝CE , CD＝BE , AC＝BC ,∴△ADC≌△CEB（SSS），（2）∵△ADC≌△CEB，∴∠ACD=∠CBE，∴CD∥BE.又∵CD=BE，∴四边形CBED是平行四边形．
1.已知四边形ABCD中有四个条件：AB∥CD，AB=CD，BC∥AD，BC=AD，从中任选两个，不能使四边形ABCD成为平行四边形的选法是 （　　）A．AB∥CD，AB=CDB．AB∥CD，BC∥AD C．AB∥CD，BC=AD D．AB=CD，BC=AD
证明：∵四边形AEFD和EBCF都是平行四边形，∴AD∥ EF，AD=EF， EF∥ BC， EF=BC.∴AD∥ BC，AD=BC.∴四边形ABCD是平行四边形.
2.四边形AEFD和EBCF都是平行四边形，求证：四边形ABCD 是平行四边形.
例3 如图，△ABC中，BD平分∠ABC，DF∥BC，EF∥AC，试问BF与CE相等吗？为什么？解：BF＝CE．理由如下：∵DF∥BC，EF∥AC，∴四边形FECD是平行四边形，∠FDB=∠DBE，∴FD=CE.∵BD平分∠ABC，∴∠FBD=∠EBD，∴∠FBD=∠FDB.∴BF=FD.∴BF＝CE.
例4 如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．求证：四边形BCED′是平行四边形.
证明：由题意得∠DAE=∠D′AE，∠DEA=∠D′EA，∠D=∠AD′E，∵DE∥AD′，∴∠DEA=∠EAD′，∴∠DAE=∠EAD′=∠DEA=∠D′EA，∴∠DAD′=∠DED′，∴四边形DAD′E是平行四边形，∴DE=AD′.
∵四边形ABCD是平行四边形，∴AB∥DC，AB=DC，∴CE∥D′B，CE=D′B，∴四边形BCED′是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA，再结合平行四边形的判定及性质进行解题.
1.四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD＝BC；③OA＝OC；④OB＝OD.从中任选两个条件，能使四边形ABCD为平行四边形的选法有(　　)A．3种　　B．4种　　C．5种　　D．6种
2.如图，在▱ABCD中，E，F分别是AB，CD的中点，连接DE，EF，BF，写出图中除▱ABCD以外的所有的平行四边形.
解：∵四边形ABCD是平行四边形,∴AD∥BC，AD=BC.∵E，F分别是AB，CD的中点，∴AE=BF=DE=FC，∴四边形ADFE是平行四边形，四边形EFCB是平行四边形，四边形BEDF是平行四边形.
1.在▱ABCD中，E、F分别在BC、AD上，若想要使四边形AFCE为平行四边形，需添加一个条件，这个条件不可以是 （　　）A．AF=CE B．AE=CF C．∠BAE=∠FCD D．∠BEA=∠FCE
2. 已知四边形ABCD中，AB∥CD，AB=CD，周长为40cm，两邻边的比是3：2，则较大边的长度是（　 ） A．8cm B．10cm C．12cm D．14cm
3.如图，在平行四边形ABCD中，EF∥AD，HN∥AB，则图中的平行四边形共有____个.
4.如图，点E，C在线段BF上，BE=CF，∠B=∠DEF，∠ACB=∠F，求证：四边形ABED为平行四边形．
证明：∵BE=CF，∴BE+EC=CF+EC．即BC=EF．又∵∠B=∠DEF,∠ACB=∠F，∴△ABC≌△DEF，∴AB=DE.∵∠B=∠DEF，∴AB∥DE．∴四边形ABED是平行四边形．
5.如图，△ABC中，AB=AC=10，D是BC边上的任意一点，分别作DF∥AB交AC于F，DE∥AC交AB于E，求DE+DF的值．
解：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴DE=AF.又∵AB=AC=10，∴∠B=∠C.∵DF∥AB，∴∠CDF=∠B，∴∠CDF=∠C，∴DF=CF，∴DE+DF=AF+FC=AC=10．
6.如图，在四边形ABCD中，AD∥BC，AD=12cm，BC=15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t(s)．（1）用含t的代数式表示： AP=_____； DP=________； BQ=________；CQ=________；
（2）当t为何值时，四边形APQB是平行四边形？
解：根据题意有AP=tcm，CQ=2tcm，PD=(12-t)cm，BQ=(15-2t)cm．∵AD∥BC，∴当AP=BQ时，四边形APQB是平行四边形．∴t=15-2t，解得t=5．∴t=5s时四边形APQB是平行四边形．
解：∵AP=tcm，CQ=2tcm，AD=12cm，∴PD=AD-AP=(12-t)cm，∵AD∥BC，∴当PD=QC时，四边形PDCQ是平行四边形．即12-t=2t，解得t=4，∴当t=4s时，四边形PDCQ是平行四边形．
（3）当t为何值时，四边形PDCQ是平行四边形？