






华师大版八年级下册2. 一次函数的图象课堂教学课件ppt
展开在未知函数图象的具体形状的情况下,怎样画出一个给定的函数的图象?一般可以分为哪几个步骤?
用“描点法”画函数图象,可以分成“列表、描点、连线”三个步骤.
根据画图象的基本步骤,要求学生分别画出y1=2x+1和y2=-2x+1的图象.
在同一个平面直角坐标系中画出下列函数的图像: (2) (3) (4)
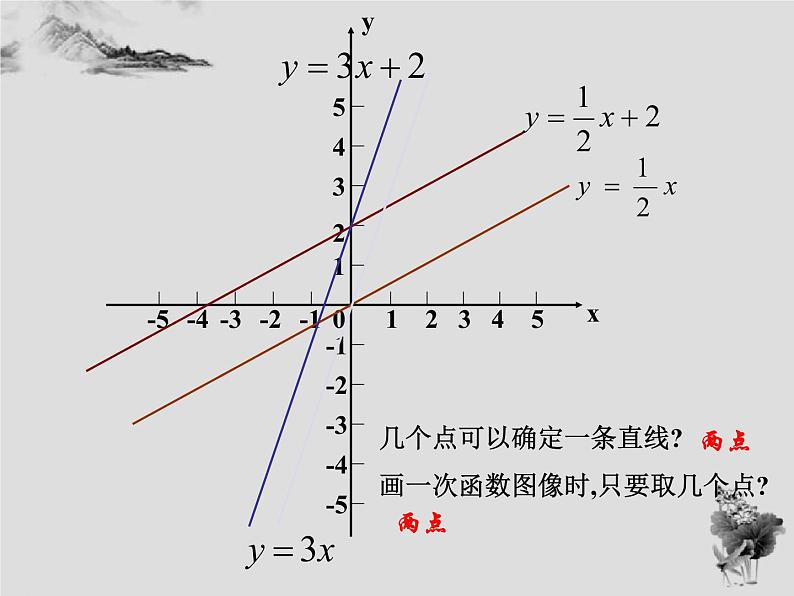
认真观察上面画出的四个函数图象的特点,比较下列各对函数图象的相同点和不同点:
观察:这些函数的图像有什么特点?
一次函数 y=kx+b(k≠0)的图象是一条直线.通常也称为直线y=kx+b .特别地,正比例函数y=kx(k≠0 )的图象是经过原点(0,0)的一条直线.值得注意的是:一次函数的图象不可能与坐标轴平行.
几个点可以确定一条直线? 画一次函数图像时,只要取几个点?
由于一次函数是直线,因此在画其图象时,只要在图象上找到两点,便可以画出它的图象,通常所取的两点是图象与坐标轴的两个交点;特别地,由于正比例函数的图象是经过原点的一条直线,因此画其图象时,只要找到异于原点(0,0)的一点的坐标即可,通常所取的点是(1,k).
特别地,由于正比例函数的图象是经过原点的一条直线,因此画其图象时,只要找到异于原点(0,0)的一点的坐标即可,通常所取的点是(1,k).
两个一次函数,当k一样、b不一样时,如 与 时,有什么共同点与不同点?
两个一次函数,当k不一样、b一样时,如 与 时,有什么共同点与不同点?
对于一次函数y=kx+b和y=k1x+b1 , (1)当k=k1,b≠b1时,两条直线平行,可以通过平移其中一条直线得到另一条直线. (2)当k≠k1,b=b1时,两条直线相交,且交点在y轴上,是(0,b).
例1在同一平面直角坐标系中画下列函数的图象:
例2求直线y= -2x-3与x轴和y轴的交点,并画出这条直线.
例3画出小明距北京的路程s与开车时间t之间函数s=570-95t的图象.
讨论: (1)这个函数是不是一次函数? (2)这个函数中自变量t的取值范围是什么?函数图象是什么? (3)在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形?能不能找出几个例子加以说明?
1 已知关于x的函数y=(m-1)x|m|+n-3
(1)当m和n取何值时,该函数是关于x的一次函数?
解: 根据一次函数的定义可知:|m|=1,且m-1≠0,故m=-1,且n为全体实数.
2.已知关于x的函数y=(m-1)x|m|+n-3
(2)当m和n取何值时,该函数是关于x的正比例函数?
解: 根据正比例函数的定义可知,在(1)的条件下还要满足n-3=0,故m=-1,n=3.
3.已知一次函数y=(6+3m)x+(m-4),y随x的增大而增大,函数的图象与y轴的交点在y轴的负半轴上,求m的取值范围.
【分析】 根据一次函数的特征可知,6+3m>0, m-4<0,解得 -2<m<4
4.直线l1和直线l2在同一直角坐标系中的位置如图所示,点P1(x1,y1)在直线l1上,点P3(x3,y3)在直线l2上,点P2(x2,y2)为直线l1,l2的交点,其中x2<x1,x2<x3则( ). A.y1<y2<y3 B.y3<y1<y2 C. y3<y2<y1 D.y2<y1<y3
【分析】 观察直线l1,y随x的增大而减小,因为x2<x1,则有y2>y1;观察直线l2知,y随x的增大而增大,因为x2<x3,则有y2<y3,故y1<y2<y3,故选A.
2、已知一次函数y=mx+|m+1|的图象与y轴交于点(0,3),且y随x值的增大而增大,则m的值为( ). A.2 B.-4 C. -2或-4 D.2或-4
3、已知一次函数y=mx-(m-2)过原点,则m的值为( ) A.m>2 B.m<2 C.m=2 D.不能确定
4、下列关系:①面积一定的长方形的长s与宽a;②圆的周长s与半径a;③正方形的面积s与边长a;④速度一定时行驶的路程s与行驶时间a,其中s是a的正比例函数的有( ) A.1个 B.2个 C.3个 D.4个
5、函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),则k= ,b= .
6、已知点A(a+2,1-a)在函数y=2x-1的图象上,求a的值.
1.一次函数的图象是一条直线.2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下移动得到,不同之处是它们与y轴的交点不同;当b一样,k不一样时,共同之处是它们与y轴交于同一点(0,b),不同之处是直线不平行.
4.一次函数y=kx+b,当x=0时,y=b;当y=0时,x= .所以直线y=kx+b与y轴的交点坐标是(0,b),与x轴的交点坐标是( ,0);5.在画实际问题中的一次函数图象时,要考虑自变量的取值范围,画出的图象往往不再是一条直线.
初中数学华师大版八年级下册3. 一次函数的性质作业ppt课件: 这是一份初中数学华师大版八年级下册3. 一次函数的性质作业ppt课件,共17页。
数学八年级下册第17章 函数及其图象17.3 一次函数2. 一次函数的图象作业ppt课件: 这是一份数学八年级下册第17章 函数及其图象17.3 一次函数2. 一次函数的图象作业ppt课件,共21页。
初中数学华师大版八年级下册4. 求一次函数的表达式教学演示ppt课件: 这是一份初中数学华师大版八年级下册4. 求一次函数的表达式教学演示ppt课件,共29页。PPT课件主要包含了一次函数,问题1,想一想,一次函数呢,b的值,待定系数法,利用图像求函数关系式,问题2,问题3等内容,欢迎下载使用。













