初中数学华师大版八年级下册18.2 平行四边形的判定教学演示ppt课件

这是一份初中数学华师大版八年级下册18.2 平行四边形的判定教学演示ppt课件，共15页。PPT课件主要包含了你有几种证明的方法等内容，欢迎下载使用。

我们学习了哪些判定平行四边形的方法？
1、平行四边形的定义：2、两组对边相等的四边形是平行四边形；3、两组对边分别相等的四边形是平行四边形 。
平行四边形的对角线具有什么性质？
平行四边形的对角线互相平分。这个命题的逆命题是什么？
已知：如图，在四边形ABCD中，对角线AC和BD相交于点O，AO＝CO， BO＝DO． 求证：四边形ABCD是平行四边形．
分析：要证明四边形ABCD是平行四边形，可以用定义，也可以用平行四边形的两条判定方法，请你选择一种方法完成证明．
对角线互相平分的四边形是平行四边形．它是真命题吗？
证明：∵OA=CO.∠AOD=∠COB(对顶角相等).∴OB=OD.∴△AOD≌△COB.∴AD=BC.同理△AOB≌△COD,∴AB=CD.∴四边形ABCD是平行四边形
例2如图，在□ABCD中， 点E、F是对角线AC上的两点，且AE＝CF， 求证：四边形BFDE是平行四边形．
分析连结BD，交AC于点O，由于OB＝OD 因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当，根据题意只需证明OE＝OF．
证明连结BD，交AC于点O ∵ 四边形ABCD是平行四边形 ∴ OB＝OD， OA＝OC。 ∵ AE＝FC，∴ OE＝OF，∴ 四边形BFDE是平行四边形（对角线互相平分的四边形是平行四边形）．
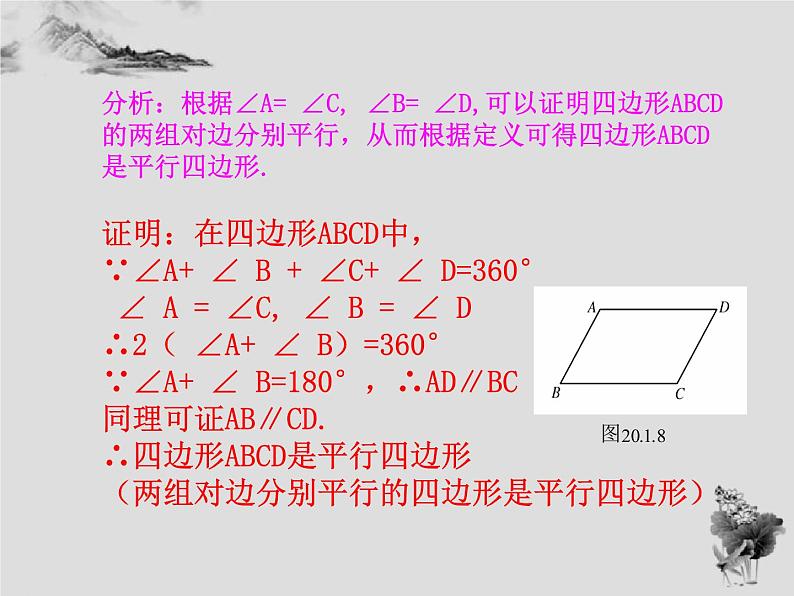
已知： 如图，四边形ABCD中，已知∠A＝∠C， ∠B＝∠D． 求证： 四边形ABCD是平行四边形．
两组对角分别相等的四边形是平行四边形。
分析：根据∠A= ∠C, ∠B= ∠D,可以证明四边形ABCD的两组对边分别平行，从而根据定义可得四边形ABCD是平行四边形.证明：在四边形ABCD中，∵∠A+ ∠ B + ∠C+ ∠ D=360° ∠ A = ∠C, ∠ B = ∠ D∴2（ ∠A+ ∠ B）=360°∵∠A+ ∠ B=180°，∴AD∥BC同理可证AB∥CD.∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）
下列条件中，不能判定四边形ABCD是平行四边形的是（ ）A.∠A=∠C，∠B=∠DB.∠A=∠B=∠C=900C.∠A+∠B=1800 ，∠B+∠C=1800D.∠A+∠B=1800 ，∠C+∠D=1800
如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．求证：四边形AECF是平行四边形．
证明：连接AC交BD于点O，∵四边形ABCD为平行四边形，∴OA=OC，OB=OD．∵BE=DF，∴OE=OF．∴四边形AECF为平行四边形．
练习如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．
1.如图所示，□AECF的对角线相交于点O，DB经过点O，分别与AE，CF交于B，D．求证：四边形ABCD是平行四边形．
证明：∵四边形AECF是平行四边形∴OE=OF，OA=OC，AE∥CF，∴∠DFO=∠BEO，∠FDO=∠EBO，∴△FDO≌△EBO，∴OD=OB，∵OA=OC，∴四边形ABCD是平行四边形．
2.已知：如图所示，平行四边形ABCD的对角线AC，BD相交于点O，EF经过点O并且分别和AB，CD相交于点E，F，点G，H分别为OA，OC的中点．求证：四边形EHFG是平行四边形．
证明：如图所示，∵点O为平行四边形ABCD对角线AC，BD的交点，
∴OA=OC，OB=OD．∵G，H分别为OA，OC的中点，∴OG= OC，∴OG=OH．
又∵AB∥CD，∴∠1=∠2．在△OEB和△OFD中，∠1=∠2，OB=OD，∠3=∠4，∴△OEB≌△OFD，∴OE=OF．∴四边形EHFG为平行四边形．
通过这节课的学习活动，你有什么收获？