初中数学华师大版八年级下册18.1 平行四边形的性质课文内容课件ppt

这是一份初中数学华师大版八年级下册18.1 平行四边形的性质课文内容课件ppt，共30页。PPT课件主要包含了讨论，如何证明，平行四边形的性质等内容，欢迎下载使用。

平行四边形是我们常见的一种图形，它具有十分和谐的对称美.它是什么样的对称图形呢？它具有哪些性质，又如何识别平行四边形呢？读下去，你就会发现这些答案了.
观察下列生活的平行四边形物体，你能说说什么是平行四边形吗？
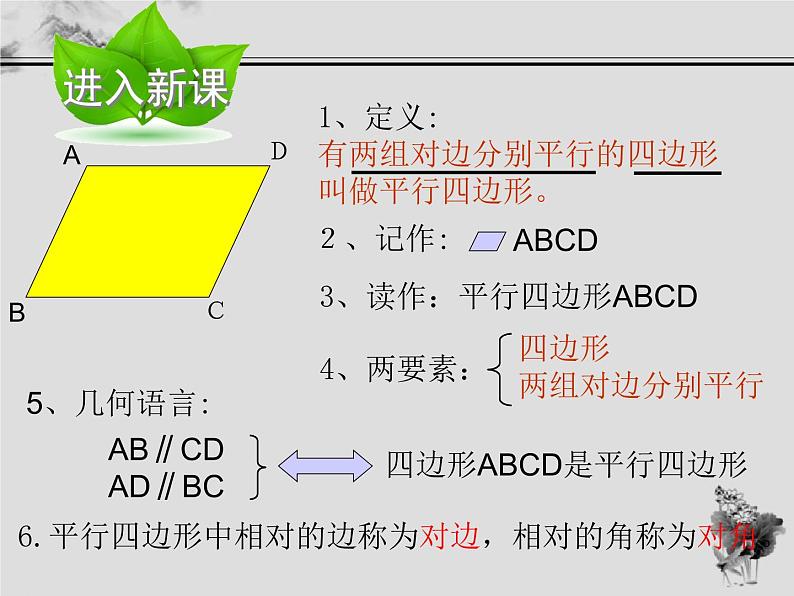
1、定义:有两组对边分别平行的四边形 叫做平行四边形。
四边形ABCD是平行四边形
AB∥CD AD∥BC
3、读作：平行四边形ABCD
6.平行四边形中相对的边称为对边，相对的角称为对角。
(1)要识别一个图形是平行四边形，目前的方法有几个？(2)平行四边形首先应该是几边形？(3)应该有几组对边平行？
定义既是性质也是判定方法，现在判定一个四边形是平行四边形的方法只有一个，就是利用定义判定.
你能从下列图形中找出平行四边形吗？说说你的理由.
剪下平行四边形，沿平行四边形的各边再在一张纸上画一个平行四边形，各顶点记为A、B、C、D.通过连接对角线得交点O，用一枚图钉穿过点O，把其中一个平行四边形绕点O旋转，观察旋转180°后的图形与原来图形是否重合.重复旋转几次，观察结果.
平行四边形是中心对称图形，对角线的交点O就是对称中心。
1.平行四边形的边具有哪些性质？说说你的理由。
2.平行四边形的角具有哪些性质？说说你的理由。
１．平行四边形对边平行且相等
猜一猜：平行四边形的性质
２．平行四边形的对角相等．
平行四边形的对边相等，对角相等.
求证：AB=CD，AD=BC，∠A=∠C，∠ABC=∠CDA.
证明：连结BD.∵四边形ABCD是平行四边形，∴AB∥DC，AD∥BC，∴∠ABD=∠CDB， ∠ADB=∠CBD.又∵ BD=DB，∴△ABD≌△CDB.∴ AB=CD，AD=BC， ∠A=∠C.由∠ABD=∠CDB和∠ADB=∠CBD得， ∠ABC=∠CDA.
平行四边形的对边相等；
平行四边形的对角相等；
∵四边形ABCD是平行四边形
平行四边形的对边平行；
如图，在 ABCD中，∠A=40°.求其他各内角的大小.
分析：要求平行四边形ABCD的各内角的大小，就是要知道∠B与∠A的关系，∠C与∠A的关系，∠D与∠A的关系.
我们知道四边形ABCD是平行四边形，那么∠A=∠C， ∠B=∠D.又因为AB∥CD ，所以∠A+∠B=180°，即得∠B=140°.同理其他角都可以求出.
如图，在 ABCD中，AB=8，周长等于24.求其余三条边的长.
分析：要求AD、BC、DC的长，就要知道这三边与已知边AB的关系，由于四边形ABCD是平行四边形，所以可得AB=DC，AD=BC.由于AB=8，所以DC=8，这样AD+BC =24-16=8，即可得到AD与BC的长.
解：在 ABCD中，AB=DC，AD=BC.∵AB=8，∴DC=8. 又∵AB+BC+DC+AD=24，∴AD=BC=4.
(1)想一想：在笔直的铁轨上，夹在两根铁轨之间的枕木是否一样长？
(2)试一试：准备一张方格纸，按下面步骤完成如下作图并按要求回答问题：
问题1：经过测量你发现 的长度有何关系？问题2：在直线AB上再取一点E，试一试.
发现：这些平行线之间的垂线段的长度相等.(1)两条直线平行，其中一条直线的任一点到另一条直线的距离，叫做这两条平行线之间的距离.(2)平行线的性质：平行线之间的距离处处相等.
如图，如果直线 l1∥ l2，那么△ABC的面积和△DBC的面积是相等的.你能说明理由吗？你还能在这两条平行线间画出其他与△ABC面积相等的三角形吗？
理由：BC共边，两直线平行，所以高相等.在直线l1上任取一点E，则△BCE的面积都与△ABC面积相等.
1. 在□ABCD中, ∠A=65°, 则∠B= °, ∠C= °, ∠D= °.
2. 在□ABCD中, AB+CD=28cm. □ABCD的周长等于96cm, 则AB= , BC= , CD= , AD= .
⒈平行四边形的两组对边分别平行。 （ ）⒉平行四边形的四个内角都相等。 （ ）⒊平行四边形的相邻两个内角的和等于180° （ ）⒋□ABCD中,如果∠A=30°，那么∠B=60° （ ）
已知平行四边形ABCD中, ∠1=15°, ∠2=25°,且AB=5cm，AO=2cm，求∠DAB和∠ABC的度数，并找出长度分别为5cm和2cm的线段.
解: ∵在□ABCD中，AB∥DC ∴∠ABD＝∠1= 15° ∴∠ABC＝15°+ 25°= 40 ° 则∠DAB＝180°- 40°= 140 ° 而 DC=AB= 5cm, CO=AO= 2cm .
在□ABCD中, ∠A=3∠B, 求∠C和∠D 的度数 .
解: ∵在□ABCD中, AD∥BC ∴∠A+∠B= 180° 又已知 ∠A=3∠B 则 3∠B +∠B= 180° 解得：∠B= 45°, ∠A=3×45°=135 ° 所以 ∠C=∠A=135 °, ∠D=∠B= 45°
已知平行四边形ABCD的周长为60cm，两邻边AB，BC长的比为3：2，求AB和BC的长度 .
解：∵在□ABCD中, 对边相等 又∵□ABCD的周长为60cm. ∴AB + BC=30cm 又AB：BC=3：2，即AB=1.5BC 则 1.5BC + BC=30 , 解得 BC=12 (cm) 而 AB=1.5×12=18 (cm)
□ABCD中, ∠DAB:∠ABC=1:3 , ∠ACD= 25°,求∠DAB, ∠DCB和∠ACB的度数 .
解：∵在□ABCD中, 相邻内角互补 又∵ ∠DAB:∠ABC=1:3 ∴ ∠DAB= 45°, ∠ABC=135° 又∵ □ABCD中，对角相等 ∴ ∠DCB =∠DAB=45° 而∠ACB=∠DCB-∠ACD= 45°- 25°= 20°
两组对边分别平行的四边形叫做 平 行 四边形。其不相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。
平行四边形的对边相等，对角相等， 相邻两角互补。