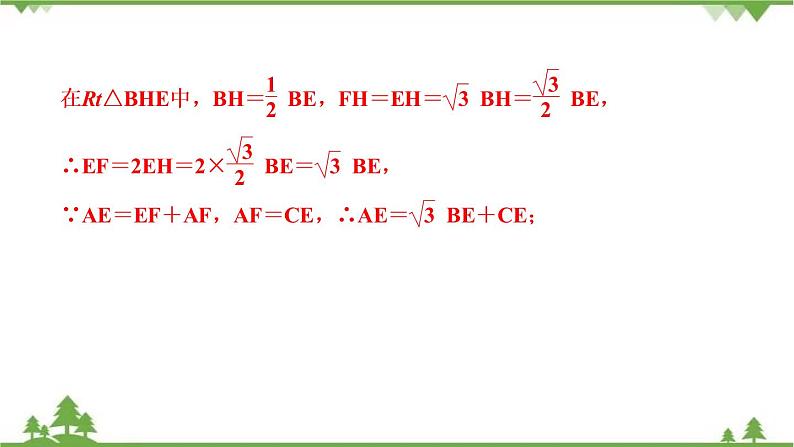
2021年中考数学总复习 拉分题训练课件 动态几何图形综合探究

这是一份2021年中考数学总复习 拉分题训练课件 动态几何图形综合探究，共50页。PPT课件主要包含了OE＝OF，AF＝2DM等内容，欢迎下载使用。

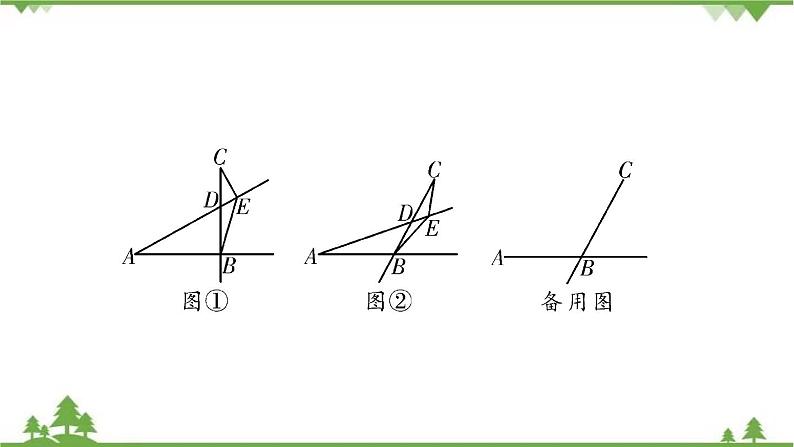
1．动点问题【例3】(2020·抚顺本溪辽阳25题12分)如图，射线AB和射线CB相交于点B，∠ABC＝α(0°＜α＜180°)，且AB＝CB.点D是射线CB上的动点(点D不与点C和点B重合)，作射线AD，并在射线AD上取一点E，使∠AEC＝α，连接CE，BE.(1)如图①，当点D在线段CB上，α＝90°时，请直接写出∠AEB的度数；(2)如图②，当点D在线段CB上，α＝120°时，请写出线段AE，BE，CE之间的数量关系，并说明理由；
∴△ABF≌△CBE(SAS)，∴∠ABF＝∠CBE，BF＝BE，∴∠ABF＋∠FBD＝∠CBE＋∠FBD，∴∠ABD＝∠FBE，∵∠ABC＝120°，∴∠FBE＝120°，∵BF＝BE，∴∠BFE＝∠BEF＝30°，∵BH⊥EF，∴∠BHE＝90°，FH＝EH，
1．(2020·岳阳)如图①，在矩形ABCD中，AB＝6，BC＝8，动点P，Q分别从C点，A点同时以每秒1个单位长度的速度出发，且分别在边CA，AB上沿C→A，A→B的方向运动，当点Q运动到点B时，P，Q两点同时停止运动．设点P运动的时间为t(s)，连接PQ，过点P作PE⊥PQ，PE与边BC相交于点E，连接QE.(1)如图②，当t＝5 s时，延长EP交边AD于点F.求证：AF＝CE；(2)在(1)的条件下，试探究线段AQ，QE，CE三者之间的等量关系，并加以证明；
(1)证明：∵四边形ABCD是矩形，∴AD∥BC，∠ABC＝90°，在Rt△ABC中，AB＝6，BC＝8，根据勾股定理得，AC＝10，由运动知，CP＝t＝5，∴AP＝AC－CP＝5，∴AP＝CP，∵AD∥BC，∴∠PAF＝∠PCE，∠AFP＝∠CEP，∴△APF≌△CPE(AAS)，∴AF＝CE；
(2)解：结论：AQ2＋CE2＝QE2，证明：如图，连接FQ，由(1)知△APF≌△CPE，∴AF＝CE，PE＝PF，∵EF⊥PQ，∴QE＝QF，在Rt△QAF中，根据勾股定理得，AQ2＋AF2＝QF2，∴AQ2＋CE2＝QE2；
(3)解：由运动知，AQ＝t，CP＝t，∴AP＝AC－CP＝10－t，∵FQ平分∠AFE，∴∠AFQ＝∠PFQ，∵∠FAQ＝∠FPQ＝90°，FQ＝FQ，∴△FAQ≌△FPQ(AAS)，∴AQ＝PQ＝t，AF＝PF，∴BQ＝AB－AQ＝6－t，∠FAC＝∠FPA，∵∠DAC＝∠ACB，∠APF＝∠CPE，∴∠ACB＝∠CPE，∴PE＝CE，
2．(2020·乐山)点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A，C重合)，分别过点A，C向直线BP作垂线，垂足分别为点E，F.点O为AC的中点．(1)如图①，当点P与点O重合时，线段OE和OF的关系是___________；(2)当点P运动到如图②所示的位置时，请在图中补全图形并通过证明判断(1)中的结论是否仍然成立？(3)如图③，点P在线段OA的延长线上运动，当∠OEF＝30°时，试探究线段CF，AE，OE之间的关系．
解：(2)补全图形如图①所示，
结论仍然成立，理由如下：延长EO交CF于点G，∵AE⊥BP，CF⊥BP，∴AE∥CF，∴∠EAO＝∠GCO，∵点O为AC的中点，∴AO＝CO，又∵∠AOE＝∠COG，∴△AOE≌△COG(AAS)，∴OE＝OG，∵∠GFE＝90°，∴OE＝OF；
(1) 证明：如图①，在AB上截取AG＝CE，∵AB＝BC，∴BG＝BE，∴∠BGE＝45°，∴∠AGE＝135°，又∵CF平分∠DCN，∴∠DCF＝45°，∴∠ECF＝135°，∴∠AGE＝∠ECF.又∵EF⊥AE，∴∠AEB＋∠FEC＝90°，∠AEB＋∠BAE＝90°，∴∠BAE＝∠FEC，
2．图形变换问题【例4】(2020·沈阳24题12分)在△ABC中，AB＝AC，∠BAC＝α，点P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，连接DB，DC.(1)如图①，当α＝60°时，①求证：PA＝DC；②求∠DCP的度数；(2)如图②，当α＝120°时，请直接写出PA和DC的数量关系；
(1)①证明：∵∠BAC＝∠BPD＝α＝60°，AB＝AC，PB＝PD，∴△ABC与△PBD都是等边三角形．∴∠PBD＝∠ABC＝60°，BA＝BC, BP＝BD .∴∠PBD－∠ABD＝∠ABC－∠ABD，∴∠PBA＝∠DBC.∴△PBA≌△DBC，∴PA＝DC；②解：∵△PBA≌△DBC，∴∠PAB＝∠DCB，∵∠BAC＝∠ACB＝60°，∴∠DCP＝120°－60°＝60°；
(1)如图①，求证：CE⊥BC；(2)连接ED，M为AC的中点，N为ED的中点，连接MN，如图②.①写出DE，AC，MN三条线段的数量关系，并说明理由；②在点D运动的过程中，当BD的长为何值时，M，E两点之间的距离最小？最小值是____，请直接写出结果．
(1)证明：如图①，过点A作AH⊥AC交BC于点H，∵∠ACB＝45°，AH⊥AC，∴∠AHC＝∠ACB＝45°，∴AH＝AC，∵将线段AD绕点A逆时针旋转90°得到线段AE，∴AD＝AE，∠HAC＝∠DAE＝90°，∴∠HAD＝∠CAE，且AD＝AE，AH＝AC，∴△HAD≌△CAE(SAS)，∴∠ACE＝∠AHD＝45°，∴∠HCE＝90°，∴CE⊥BC；
2．(2020·邵阳)已知：如图①，将一块45°角的直角三角板DEF与正方形ABCD的一角重合，连接AF，CE，点M是CE的中点，连接DM.(1)请你猜想AF与DM的数量关系是____________；(2)如图②，把正方形ABCD绕着点D顺时针旋转α角(0°＜α＜90°).①AF与DM的数量关系是否仍成立，若成立，请证明；若不成立，请说明理由；(温馨提示：延长DM到点N，使MN＝DM，连接CN)②求证：AF⊥DM；
(2)①解：AF＝2DM仍然成立，证明：延长DM到点N，使MN＝DM，连接CN，∵M是CE中点，∴CM＝EM，又∠CMN＝∠EMD，∴△MNC≌△MDE(SAS)，∴CN＝DE＝DF，∠MNC＝∠MDE，∴CN∥DE，又AD∥BC，∴∠NCB＝∠EDA，∵四边形ABCD是正方形，∴AD＝DC，∠BCD＝90°＝∠EDF，∴∠ADF＝∠DCN，∴△ADF≌△DCN(SAS)，∴AF＝DN，∴AF＝2DM；
解：(1)如图①，取AC的中点M，连接EM，BF，∵AB＝AC，∠BAC＝60°，∴△ABC为等边三角形，∵线段CE绕点E顺时针旋转60°得到线段EF，∴EC＝EF，∠CEF＝60°，∴△EFC是等边三角形，∴EC＝CF，∠ACB＝∠ECF＝60°，∴∠ACE＝∠BCF，∵AC＝BC，∴△ACE≌△BCF(SAS)，
∵D是BC 的中点，M是AC的中点，∴DF＝EM，∵E是AD的中点，M是AC的中点，
4．(2019·济宁)如图①，在矩形ABCD中，AB＝8，AD＝10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G.(1)求线段CE的长；(2)如图②，M，N分别是线段AG，DG上的动点(与端点不重合)，且∠DMN＝∠DAM，设AM＝x，DN＝y.①写出y关于x的函数解析式，并求出y的最小值；②是否存在这样的点M，使△DMN是等腰三角形？若存在，请求出x的值；若不存在，请说明理由．