初中第十九章 一次函数综合与测试优秀测试题

这是一份初中第十九章 一次函数综合与测试优秀测试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一 选择题


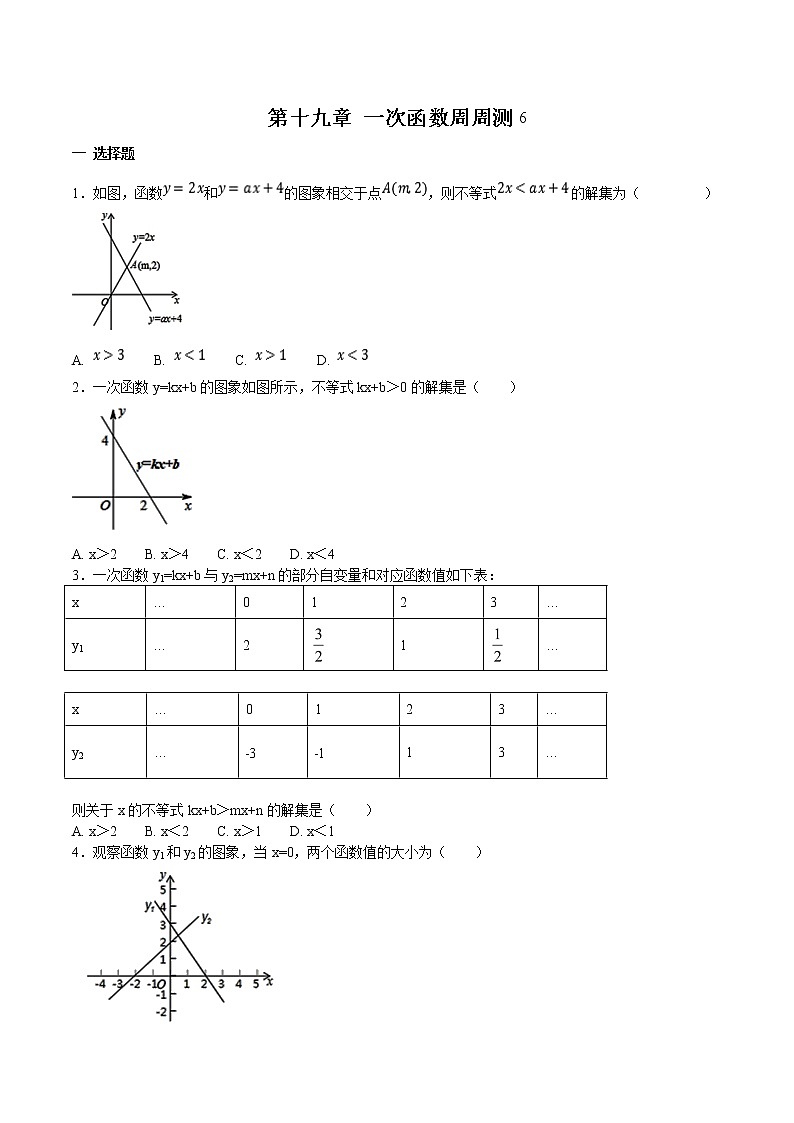
1．如图，函数和的图象相交于点，则不等式的解集为（ ）





A. B. C. D.


2．一次函数y=kx+b的图象如图所示，不等式kx+b＞0的解集是（ ）





A. x＞2 B. x＞4 C. x＜2 D. x＜4


3．一次函数y1=kx+b与y2=mx+n的部分自变量和对应函数值如下表：








则关于x的不等式kx+b＞mx+n的解集是（ ）


A. x＞2 B. x＜2 C. x＞1 D. x＜1


4．观察函数y1和y2的图象，当x=0，两个函数值的大小为（ ）





A. y1＞y2 B. y1＜y2 C. y1=y2 D. y1≥y2


5.6月份以来，猪肉价格一路上涨．为平抑猪肉价格，某省积极组织货源，计划由A、B、C三市分别组织10辆、10辆和8辆运输车向D、E两市运送猪肉，现决定派往D、E两地的运输车分别是18辆、10辆，已知一辆运输车从A市到D、E两市的运费分别是200元和800元，从B市到D、E两市的运费分别是300元和700元，从C市到D、E两市的运费分别是400元和500元．若设从A、B两市都派x辆车到D市，则当这28辆运输车全部派出时，总运费W（元）的最小值和最大值分别是（ ）


A． 8000，13200 B．9000，10000 C．10000，13200 D．13200，15400


6．如图，是一对变量满足的函数关系的图象．有下列3个不同的问题情境：





①小明骑车以400米/分的速度匀速骑了5分钟，在原地休息了4分钟，然后以500米/分的速度匀速骑回出发地，设时间为x分钟，离出发地的距离为y千米；


②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个桶注水，注5分钟后停止，等4分钟后，再以2升/分的速度匀速倒空桶中的水，设时间为x分钟，桶内的水量为y升；


③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S△ABP；当点P与点A重合时，y=0，


其中，符合图中所示函数关系的问题情境的个数为（ ）


A．0 B．1 C．2 D．3


7.．甲、乙二人从学校出发去科技馆，甲步行一段时间后，乙骑自行车沿相同路线行进，两人均匀速前行，他们的路程差s（米）与甲出发时间t（分）之间的函数关系如图所示．下列说法：①乙先到达青少年宫；②乙的速度是甲速度的2.5倍；③b=480；④a=24．其中正确的是（ ）





A．①②③B．①②④ C．①③④ D．①②③④


二 填空题


8．如图，平面直角坐标系中，经过点B（﹣4，0）的直线y=kx+b与直线y=mx+2相交于点A(-,-1)，则不等式mx+2＜kx+b＜0的解集为_____．





9．函数y=kx+b的图象如图所示，则方程kx+b=0的解为________，不等式kx+b>0的解集为_________，不等式kx+b－3>0的解集为________．





10．一次函数y=kx+b的图象经过A(-1，1）和B(- ，0），则不等式组的解为________________.





11．已知一次函数的图象过点与，那么这个函数的解析式是__________，则该函数的图象与轴交点的坐标为__________________.


12．如图，直线y＝kx＋b上有一点P(－1，3)，回答下列问题：


(1)关于x的方程kx＋b＝3的解是_______．


(2)关于x的不等式kx＋b>3的解是________．


(3)关于x的不等式kx＋b－3<0的解是______．


(4)求不等式－3x≥kx＋b的解．


(5)求不等式(k+3)x＋b>0的解．








三 解答题


13．画出函数y＝2x－4的图象，并回答下列问题：


(1)当x取何值时，y＞0?


(2)若函数值满足－6≤y≤6，求相应的x的取值范围．


















































14．已知：直线与轴交于点，与轴交于点，坐标原点为．


（）求点，点的坐标．


（）求直线与轴、轴围成的三角形的面积．


（）求原点到直线的距离．





























15．在平面直角坐标系中，已知一次函数与相交于点，且与轴交于点．


（1）求一次函数和的解析式；


（2）当时，求出的取值范围．





























16．已知直线y=kx+5交x轴于A，交y轴于B且A坐标为（5，0），直线y=2x﹣4与x轴于D，与直线AB相交于点C．


（1）求点C的坐标；


（2）根据图象，写出关于x的不等式2x﹣4＞kx+5的解集；


（3）求△ADC的面积．






































17．水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃，他了解到猕猴桃有精品盒与普通盒两种包装，精品盒的批发价格每盒60元，普通盒的批发价格每盒40元，现小李购得精品盒与普通盒共60盒，费用共为3100元。


（1）问小李分别购买精品盒与普通盒多少盒？


（2）小李经营着甲、乙两家店铺，每家店铺每天部能售出精品盒与普通盒共30盒，并且每售出一盒精品盒与普通盒，在甲店获利分别为30元和40元，在乙店获利分别为24元和35元．现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒，设分配给甲店精品盒a盒，请你根据题意填写下表：


小李希望在甲店获利不少于1000元的前提下，使自己获取的总利润W最大，应该如何分配？最大的总利润是多少？








18．某公司在甲、乙两座仓库分别有农用车12辆和6辆，现要调往A县10辆，调往B县8辆，已知调运一辆农用车的费用如表：


（1）设从乙仓库调往A县农用车x辆，求总运费y关于x的函数关系式。


（2）若要求总运费不超过900元．共有哪几种调运方案？


（3）求出总运费最低的调运方案，最低运费是多少元？


x
…
0
1
2
3
…
y1
…
2
1
…
x
…
0
1
2
3
…
y2
…
﹣3
﹣1
1
3
…
精品盒数量（盒）
普通盒数量（盒）
合计（盒）
甲店
a

30
乙店


30
县名费用仓库
A
B
甲
40
80
乙
30
50
第十九章 一次函数周周测6试题答案


1．B


【解析】∵函数的图象经过点，


∴，


解得：，


∴点，


当时，，


即不等式的解集为．


故选：．


2．C


【解析】kx+b＞0即是一次函数的图象在x轴的上方，由图象可得x＜2，故选C.


3．B


【解析】根据表可得 中y随x的增大而减小；


中y随x的增大而增大．且两个函数的交点坐标是（2，1）．


则当 时，


故选B．


4．A


【解析】由图可知：当x=0时，y1=3，y2=2，


y1＞y2 ．


故选A．


5．D


【解析】由图象知,函数y=3x+1与x轴交于点即当x＞时,函数值y的范围是y＞0,因而当y＞0时,x的取值范围是x＞,函数y=3x+1与x轴交于点（2,0）,即当x＜2时,函数值y的范围是y＞0,因而当y＞0时,x的取值范围是x＜2,所以,原不等式组的解集是＜x＜2,故选D.


6．B


【解析】根据图形，找出直线y1在直线y2上方部分的x的取值范围即可．


解：由图形可，当x>−1时,k1x+m>k2x+n，


即(k1−k2)x>−m+n，


所以，关于x的不等式(k1−k2)x>−m+n的解集是x>−1.


故选B.


7．C


【解析】由于方程kx+b=0的解是x=3，即x=3时，y=0，所以直线y=kx+b经过点（3，0），


故选C.


8．﹣4＜x＜﹣


【解析】根据函数的图像，可知不等式mx+2＜kx+b＜0的解集就是y=mx+2在函数y=kx+b的下面，且它们的值小于0的解集是﹣4＜x＜﹣.


故答案为：﹣4＜x＜﹣.


9． x=1 x<1 x<0


【解析】由图可知，函数y=kx+b的图象和x轴相交于点（1，0），和y轴相交于点（0，3），


∴方程kx+b=0的解为：x=1；


不等式kx+b>0的解集为：x<1；


不等式kx+b－3>0的解集为：x<0.


故答案为：(1). x=1 (2). x<1 (3). x<0.


10．-

【解析】由题意可得：一次函数图象在y=1的下方时x＜-1，在y=0的上方时x＞-，


∴关于x的不等式0＜kx+b＜1的解集是-＜x＜-1．


故答案为：-＜x＜1．


11． y=2x-1 (0，-1)


【解析】设该一次函数的解析式为y=kx+b (k≠0).


将点(3, 5)和(-4, -9)分别代入该一次函数的解析式，得


，


解之，得


，


∴该一次函数的解析式为y=2x-1.


∵函数图象与y轴交点的横坐标为零，


又∵当x=0时， ，


∴该函数的图象与y轴交点的坐标为(0, -1).


故本题应依次填写：y=2x-1；(0, -1).


12．(1)x＝－1;(2)x＞－1;(3)x＜－1;(4)x≤－1;(5)x＞－1.


解析：（1）因为P(-1，3)在一次函数y=kx＋b图像上，所以kx＋b＝3得解为x=-1.


(2) 不等式kx＋b>3,恰好是一次函数y=kx＋b函数值大于3的部分，对应的x＞－1.


(3)因为 kx＋b－3<0所以kx＋b<3, 恰好是一次函数y=kx＋b函数值大小于3的部分对应的x<－1.


(4)观察图象可知，点(－1，3)在函数y＝－3x上，构造函数y＝－3x如解图．y＝－3x比y=kx＋b图像“高”的部分，


∴不等式－3x≥kx＋b的解为x≤－1.


(5)不等式(k＋3)x＋b＞0可变形为kx＋b＞－3x，仿照(4)可得x＞－1.


13．函数y=2x-4的图象如图所示：





（1）令y=0，则2x-4=0，


解得：x=2


由图象得：当x>2时，y>0；


（2）当y=6时，则2x-4=6


解得：x=5；


当y=-6时，则2x-4=-6


解得：x=-1


∵－6≤y≤6，


∴－1≤x≤5.


14．（）∵，


当时，，


．


∴．


当时，，


∴．


（）∵


∴


∴


（）作于点．





∵


,


∴,


∴





,


∴点到直线的距离为．


15．∵一次函数过点


∴


∴；


又∵一次函数经过点，


∴；


解得：


∴；


（2）.


16．（1）根据点A的坐标利用待定系数法可求出直线AB的解析式，联立直线AB、CD的解析式方程组，通过解方程即可求出点C的坐标；


（2）根据直线AB、CD的上下位置关系结合点C的坐标，即可得出不等式2x-4>kx+5的解集；


（3）利用一次函数图形上点的坐标特征可求出点D的坐标，再根据三角形的面积公式即可求出△DC的面积.


解：（1）∵直线y=kx+5经过点A（5，0），


∴5k+5＝0


解得k＝-1


∴直线AB的解析式为：y=-x+5； ，


解得： ，


∴点C（3，2）


（2）观察函数图象可知：当x>3时，直线y=2x-4在直线y=-x+5的上方，


∴不等式2x-4>kx+5的解集为x>3.


（3）把y=0代入y=2x﹣4得2x﹣4=0.


解得x=2∴D（2，0）


∵A（5，0），C（3，2）


∴AD=3


S△ADC =32=3