八年级下册16.3 二次根式的加减优秀课件ppt

这是一份八年级下册16.3 二次根式的加减优秀课件ppt，共33页。PPT课件主要包含了回顾旧知，新课导入，教学目标，教学重难点，化成最简二次根式，分配律，小练习，三合并，课堂小结等内容，欢迎下载使用。

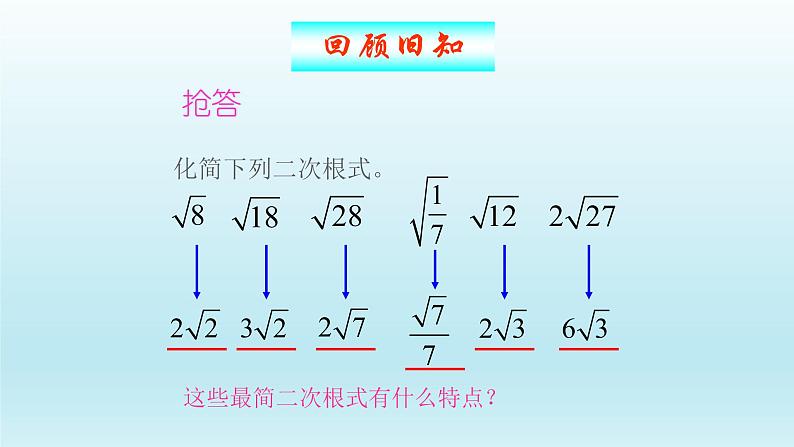
化简下列二次根式。
这些最简二次根式有什么特点？
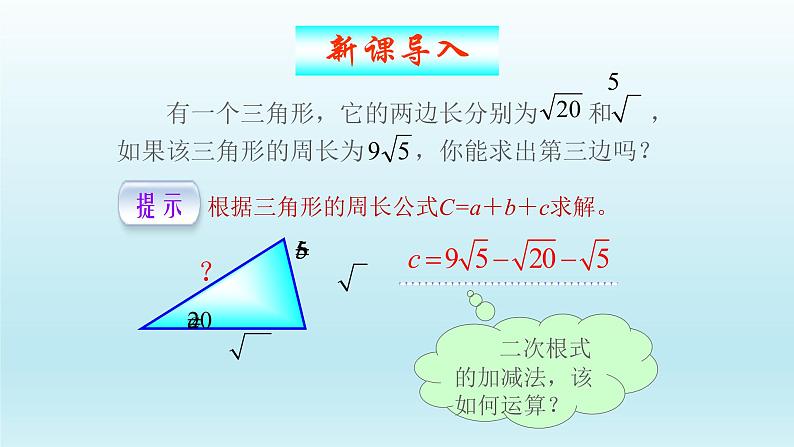
有一个三角形，它的两边长分别为 和 ，如果该三角形的周长为 ，你能求出第三边吗？
根据三角形的周长公式C=a＋b＋c求解。
二次根式的加减法，该如何运算？
【知识与能力】了解最简二次根式的概念并灵活运用它们对二次根式进行加减。 　　
【过程与方法】通过分析前面的计算和化简结果，抓住它们的共同特点，给出最简二次根式的概念。利用最简二次根式的概念，来对相同的二次根式进行合并，达到对二次根式进行计算和化简的目的。
【情感态度与价值观】 利用规定准确计算和化简的严谨的科学精神。经过探索二次根式的重要结论，发展学生观察、分析、发现问题的能力。
二次根式化简为最简二次根式以及二次根式的判定。二次根式的加减、乘除、乘方等运算规律。由整式运算知识迁移到含二次根式的运算。
二次根式的加减类似于什么运算？
以上，是我们以前所学的整式加减——同类项合并。同类项合并就是字母不变，系数相加减。
加法交换律：a+b=b+a乘法交换律：a×b=b×a加法结合律：a+b+c=(a+b)+c=a+(b+c)乘法结合律：(a×b)×c=a×(b×c)左分配律：c·(a+b)=(c·a)+(c·b)右分配律：(a+b)·c=(a·c)+(b·c)
现有一块长7.5dm、宽5dm的木板，能否在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板？
这两块正方形木板的边长分别为
这两块正方形边长的和为
∴木板够长，可以截出这两个正方形木板。
几个二次根式化成最简二次根式后，如果被开方数相同，这几个二次根式就叫做同类二次根式。
判断一组式子是否为同类二次根式，只需看化为最简二次根式后的被开方数是否相同，与最简二次根式前面的因式及符号无关。
1.说出 的三个同类二次根式。
2.下列各式中哪些是同类二次根式？
（1）如果几个二次根式的被开方数相同，那么可以直接根据分配律进行加减运算。
（2）如果所给的二次根式不是最简二次根式，应该先化简，再进行加减运算。
二次根式加减运算的步骤
（3）合并同类二次根式。
（1）将每个二次根式化为最简二次根式。
（2）找出其中的同类二次根式。
如图所示的Rt△ABC中，∠B=90°，点P从点B开始沿BA边以1cm/s的速度向点A移动。同时，点Q也从点B开始沿BC边以2cm/s的速度向点C移动。问：几秒后△PBQ的面积为35cm2？PQ的距离是多少厘米？（结果用最简二次根式）
解：设x秒后△PBQ的面积为35cm2，
则有PB=x，BQ=2x。
（1）加减与乘除的混合运算，先乘除，后加减，使难点分散。
（2）在运算中，对于各根式不一定要先化简，而是先乘除，进行约分，达到化简的目的，但最后结果一定要化简。
观察算式，找出特征，利用多项式乘法法则和乘法公式求解。
如果分母是二次根式，采用分子、分母同乘以分母的的方法进行化简。
（依据分式的基本性质）
如果分母是含二次根式的两个因式的和或差，怎样化简？
分母乘以什么样的式子，就能将分母的根号去掉？
如果分母是含二次根式的两个因式的和或差，采用分子、分母同乘以分母的有理化因式的方法进行化简。
辨别是否互为有理化因式
有关二次根式的除法，可先写成分式的形式，然后通过分母有理化进行运算。
2.二次根式加减运算的步骤：
（1）单独一项 的有理化因式就是它本身 。
（2）出现和、差形式的：如 的有理化因式为