2018版高考数学（人教a版理科）一轮复习真题演练集训：第四章　三角函数与解三角形 4-8 word版含答案

这是一份2018版高考数学（人教a版理科）一轮复习真题演练集训：第四章　三角函数与解三角形 4-8 word版含答案，共6页。
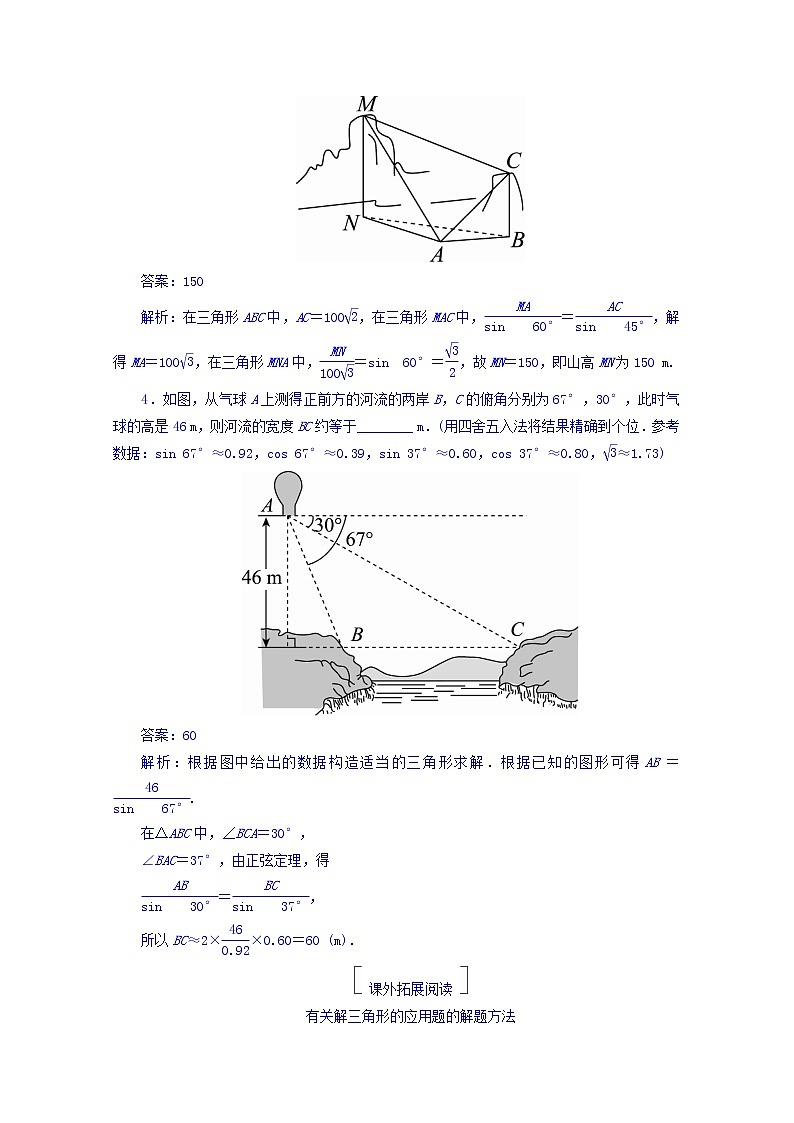
 www.ks5u.com 真题演练集训 1．如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成角)．若AB＝15 m，AC＝25 m，∠BCM＝30°，则tan θ的最大值是(　　)A.   B.  C.   D.答案：D解析：如图，过点P作PO⊥BC于点O，连接AO，则∠PAO＝θ.设CO＝x m，则OP＝x m.在Rt△ABC中，AB＝15 m，AC＝25 m，所以BC＝20 m．所以cos ∠BCA＝.所以AO＝＝(m)．所以tan θ＝＝＝.当＝，即x＝时，tan  θ取得最大值为＝.2．如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD＝________m. 答案：100解析：由题意，在△ABC中，∠BAC＝30°，∠ABC＝180°－75°＝105°，故∠ACB＝45°.又AB＝600 m，故由正弦定理得＝，解得BC＝300 m.在Rt△BCD中，CD＝BC·tan  30°＝300×＝100(m)．3．如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN＝60°，C点的仰角∠CAB＝45°以及∠MAC＝75°；从C点测得∠MCA＝60°，已知山高BC＝100 m，则山高MN＝________m.答案：150解析：在三角形ABC中，AC＝100，在三角形MAC中，＝，解得MA＝100，在三角形MNA中，＝sin  60°＝，故MN＝150，即山高MN为150 m.4．如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46 m，则河流的宽度BC约等于________ m．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80，≈1.73)答案：60解析：根据图中给出的数据构造适当的三角形求解．根据已知的图形可得AB＝.在△ABC中，∠BCA＝30°，∠BAC＝37°，由正弦定理，得＝，所以BC≈2××0.60＝60 (m)． 课外拓展阅读 有关解三角形的应用题的解题方法1．解决关于解三角形的应用问题的步骤2．解三角形的应用题的两种情形及解题方法    (1)实际问题经抽象概括后，已知量与未知量全部集中在一个三角形中，可用正弦定理或余弦定理求解；    (2)实际问题经抽象概括后，已知量与未知量涉及两个或两个以上三角形，这时需作出(或找出)这些三角形，先解能直接解的三角形，然后逐步求出其他三角形的解，有时需设出未知量，利用几个三角形中边角所满足的关系列出方程(组)，解方程(组)得出所要求的解．3．解决关于解三角形的应用问题应注意的事项    (1)要注意仰角、俯角、方位角以及方向角等名词，并能准确地找出这些角；    (2)要注意将平面几何中的性质、定理与正弦、余弦定理结合起来使用，这样可以优化解题过程；    (3)注意题目中的隐含条件以及解的实际意义．　如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m/min.在甲出发2 min后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min，山路AC长为1260 m，经测量，cos A＝，cos C＝.(1)求索道AB的长；(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？ (3)为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？　(1)在△ABC中，因为cos A＝，cos C＝，所以sin A＝，sin C＝.从而sin B＝sin＝sin(A＋C)＝sin Acos C＋cos Asin C＝×＋×＝.由＝，得AB＝×sin C＝×＝1 040(m)．所以索道AB的长为1 040 m.(2)设乙出发t分钟后，甲、乙两游客距离为d，此时，甲行走了(100＋50t) m，乙距离A处130t m，所以由余弦定理，得d2＝(100＋50t)2＋(130t)2－2×130t×(100＋50t)×＝200(37t2－70t＋50)，因为0≤t≤，即0≤t≤8，故当t＝(min)时，d最小，所以乙出发分钟后，甲、乙两游客距离最短．(3)由＝，得BC＝×sinA＝×＝500(m)．乙从B出发时，甲已走了50×(2＋8＋1)＝550(m)，还需走710 m才能到达C.设乙步行的速度为v m/min，由题意得－3≤－≤3，解得≤v≤，所以为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在(单位：m/min)范围内．