高中人教版 (新课标)6.向心力课时作业

这是一份高中人教版 (新课标)6.向心力课时作业，共12页。试卷主要包含了关于向心力的说法中正确的是等内容，欢迎下载使用。
1．关于向心力的说法中正确的是( )


A．物体受到向心力的作用才能做圆周运动


B．向心力是指向圆心方向的合外力，它是根据力的作用效果命名的


C．向心力可以是重力、弹力、摩擦力等各种力的合力，也可以是某种力的分力


D．向心力只改变物体的运动方向，不可能改变物体运动的快慢


解析 向心力是根据力的作用效果命名的，而不是一种性质力，物体之所以能做匀速圆周运动，不是因为物体多受了一个向心力的作用，而是物体所受各种力的合外力始终指向圆心，从而只改变速度的方向而不改变速度的大小，故选项A错误，B、C、D三个选项正确．


答案 BCD


2．用长短不同、材料相同的同样粗细的绳子，各拴着一个质量相同的小球在光滑水平面上做匀速圆周运动，那么( )


A．两小球以相同的线速度运动时，长绳易断


B．两小球以相同的角速度运动时，长绳易断


C．两小球以相同的角速度运动时，短绳易断


D．不管怎样，都是短绳易断


解析 绳子最大承受拉力相同，由向心力公式F＝mω2r＝eq \f(mv2,r)可知，角速度相同，半径越大，向心力越大，故B选项正确．


答案 B


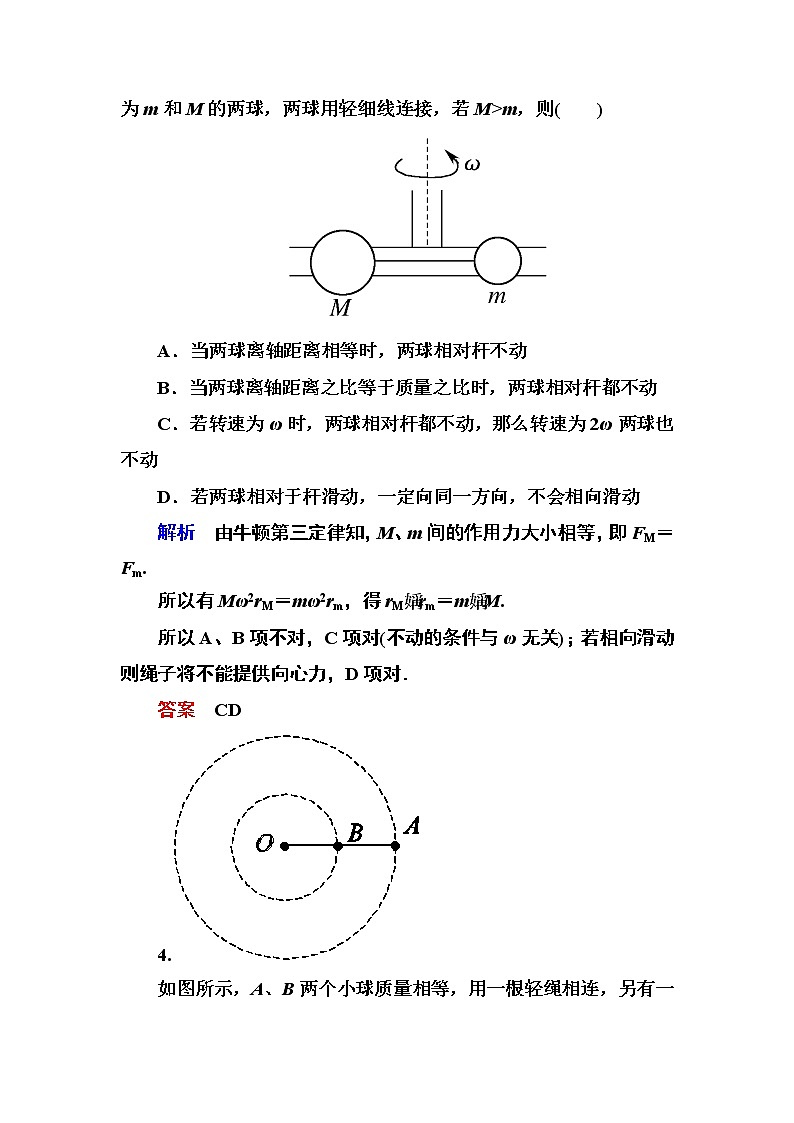
3．如图所示，在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球，两球用轻细线连接，若M>m，则( )





A．当两球离轴距离相等时，两球相对杆不动


B．当两球离轴距离之比等于质量之比时，两球相对杆都不动


C．若转速为ω时，两球相对杆都不动，那么转速为2ω两球也不动


D．若两球相对于杆滑动，一定向同一方向，不会相向滑动


解析 由牛顿第三定律知，M、m间的作用力大小相等，即FM＝Fm.


所以有Mω2rM＝mω2rm，得rMrm＝mM.


所以A、B项不对，C项对(不动的条件与ω无关)；若相向滑动则绳子将不能提供向心力，D项对．


答案 CD


4.


如图所示，A、B两个小球质量相等，用一根轻绳相连，另有一根轻绳的两端分别连接O点和B点，让两个小球绕O点在光滑水平桌面上以相同的角速度做圆周运动，若OB绳上的拉力为F1，AB绳上的拉力为F2，OB＝AB，则( )


A．F1:F2＝2:3 B．F1:F2＝3:2


C．F1:F2＝5:3 D．F1:F2＝2:1


解析 小球在光滑水平桌面上做匀速圆周运动，设角速度为ω，在竖直方向上所受重力与桌面支持力平衡，水平方向不受摩擦力，绳子的拉力提供向心力．由牛顿第二定律，对A球有F2＝mr2ω2，对B球有F1－F2＝mr1ω2，已知r2＝2r1，各式联立解得F1＝eq \f(3,2)F2，故B对，A、C、D错．


答案 B





5．质量为m的A球在光滑水平面上做匀速圆周运动，小球A用细线拉着，细线穿过板上光滑小孔O，下端系一相同质量的B球，如图所示，当平板上A球绕O点分别以ω和2ω角速度转动时，A球距O点距离之比是( )


A．1:2 B．1:4


C．4:1 D．2:1


解析 A球做圆周运动的向心力大小等于B球重力．由F＝mω2r向心力相同，得


eq \f(ω\\al(2,1),ω\\al(2,2))＝eq \f(r2,r1)＝eq \f(ω2,2ω2)＝eq \f(1,4).


答案 C


6．游客乘坐过山车，在圆弧轨道最低点处获得向心加速度达20 m/s2，g取10 m/s2，那么此位置的座椅对游客的作用力相当于游客重力的( )


A．1倍 B．2倍


C．3倍 D．4倍





解析 游客乘坐过山车在圆弧轨道最低点的受力如图所示，


由牛顿第二定律得，


FN－mg＝man，


FN＝man＋mg＝3 mg，


故C选项正确．


答案 C


7.


一质量为m的物体，沿半径为R的向下凹的圆形轨道滑行，如图所示，经过最低点时速度为v，物体与轨道之间的动摩擦因数为μ，则它在最低点时受到的摩擦力为( )


A．μmg B.eq \f(μmv2,R)


C．μmeq \b\lc\(\rc\)(\a\vs4\al\c1(g＋\f(v2,R))) D．μmeq \b\lc\(\rc\)(\a\vs4\al\c1(g－\f(v2,R)))


解析 在最低点由向心力公式FN－mg＝meq \f(v2,R)，得FN＝mg＋meq \f(v2,R)，又由摩擦力公式F＝μFN＝μmeq \b\lc\(\rc\)(\a\vs4\al\c1(g＋\f(v2,R)))，C对．


答案 C


8．如图所示，光滑杆偏离竖直方向的夹角为α，杆以O为支点绕竖直线旋转，质量





为m的小球套在杆上可沿杆滑动，当杆角速度为ω1时，小球旋转平面在A处，当杆角速度为ω2时，小球旋转平面在B处，设杆对小球的支持力在A、B处分别为FN1、FN2，则有( )


A．FN1＝FN2


B．FN1>FN2


C．ω1ω2





解析 小球做圆周运动的向心力由小球重力和杆的弹力的合力提供，垂直轨迹平面方向的合力为零，即如图


FNsinα＝mg，


FNcsα＝mω2r，


解得mω2r＝mgctα，ω＝ eq \r(\f(gctα,r)).


故FN1＝FN2，ω1>ω2，选项A、D正确．


答案 AD





9．如图所示，圆盘上叠放着两个物块A和B.当圆盘和物块绕竖直轴匀速转动时，物块与圆盘始终保持相对静止，则( )


A．A物块不受摩擦力作用


B．物块B受5个力作用


C．当转速增大时，A受摩擦力增大，B所受摩擦力也增大


D．A对B的摩擦力方向沿半径指向转轴


解析 A物块做匀速圆周运动，一定需要向心力，向心力只可能由B对A的静摩擦力提供，故A选项错误；B物体做匀速圆周运动，受到重力、圆盘的支持力、圆盘的静摩擦力，A对B物体的压力和静摩擦力，故B选项正确；当转速增大时，A、B所受向心力均增大，故C选项正确；A对B的静摩擦力背向圆心，故D选项错误．


答案 BC





10．甲、乙两名溜冰运动员，M甲＝80 kg，M乙＝40 kg，面对面拉着弹簧秤做圆周运动的溜冰表演，如图所示，两人相距0.9 m，弹簧秤的示数为9.2 N，下列判断中正确的是( )


A．两人的线速度相同，约为40 m/s


B．两人的角速度相同，为6 rad/s


C．两人的运动半径相同，都是0.45 m


D．两人的运动半径不同，甲为0.3 m，乙为0.6 m


解析 甲、乙两人受到的向心力大小相等，绕两者连线上某一点做匀速圆周运动，其角速度相等，由


Fn＝mω2r可知m甲ω2r甲＝m乙ω2r乙，


r甲＋r乙＝0.9 m.


解得r甲＝0.3 m，r乙＝0.6 m，故D选项正确；


ω＝ eq \r(\f(Fn,mr))＝ eq \r(\f(9.2,80×0.3)) rad/s＝ eq \r(\f(2.3,6)) rad/s，故B选项错误．


答案 D





11．如图所示，在匀速运动的水平圆盘上，沿半径方向放着用细线相连的质量相等的两个物体A和B，它们与盘间的摩擦因数相同，当圆盘转动到两个物体刚好还未发生滑动时，烧断细线，两个物体的运动情况是( )


A．两物体沿切向方向滑动


B．两物体均沿半径方向滑动，离圆盘圆心越来越远


C．两物体仍随圆盘一起做圆周运动，不发生滑动


D．物体B仍随圆盘一起做匀速圆周运动，物体A发生滑动，离圆盘圆心越来越远


解析 当圆盘转动到两个物体刚好未发生滑动时，设圆盘的角速度为ω，则A、B两物体随圆盘转动的角速度都为ω，由于rA>rB，根据Fn＝mω2r.可知，A物体的向心力FnA大于B物体做圆周运动的向心力FnB，且FnA＝f＋T，FnB＝f－T.其中T为绳的拉力，f为A、B物体受到圆盘的最大静摩擦力，当线烧断后，B物体受到静摩擦力随圆盘做匀速圆周运动，而A物体由于所受最大静摩擦力不是提供其椭圆转动的向心力，从而使其发生滑动，做离心运动，离圆盘圆心越来越远，故选项D正确．


答案 D


12．原长为L的轻弹簧一端固定一小铁块，另一端连接在竖直轴OO′上，弹簧的劲度系数为k，小铁块放在水平圆盘上，若圆盘静止，把弹簧拉长后将小铁块放在圆盘上，使小铁块能保持静止的弹簧的最大长度为5L/4，现将弹簧长度拉长到6L/5后，把小铁块放在圆盘上，在这种情况下，圆盘绕其中心轴OO′以一定角速度匀速转动，如图所示，已知小铁块的质量为m，为使小铁块不在圆盘上滑动，圆盘转动的角速度ω最大不得超过多少？





解析 以小铁块为研究对象，圆盘静止时，设铁块受到的最大静摩擦力为fm，有fm＝kL/4.


圆盘转动的角速度ω最大时，铁块受到的摩擦力f与弹簧的拉力kx的合力提供向心力，由牛顿第二定律得kx＋fm＝m(6L/5)ω2.


又x＝L/5，


解以上三式得角速度的最大值ω＝eq \r(3k/8m).


答案 eq \r(3k/8m)


13．如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面，则此时绳的拉力是多少？若要小球离开锥面，则小球的角速度至少多大？





解析 小球在锥面上受到拉力、支持力、重力的作用，如图所示．建立如图所示的平面直角坐标系．





对其受力进行正交分解．


在y轴方向，根据平衡条件，得


Fcsθ＋FNsinθ＝mg，


在x轴方向，根据牛顿第二定律，得


Fsinθ－FNcsθ＝mLω2sinθ，


解得F＝m(gcsθ＋Lω2sin2θ)．


要使球离开锥面，则


FN＝0，解得ω＝ eq \r(\f(g,Lcsθ)).


答案 m(gcsθ＋Lω2sin2θ) eq \r(\f(g,Lcsθ))





14．如图所示，两绳系一个质量为m＝0.1 kg的小球．上面绳长l＝2 m，两绳都拉直时与轴夹角分别为30°与45°.问球的角速度满足什么条件，两绳始终张紧？





解析 分析两绳始终张紧的制约条件：当ω由零逐渐增大时可能出现两个临界值，其一是BC恰好拉直，但不受拉力；其二是AC仍然拉直，但不受拉力．设两种情况下的转动角速度分别为ω1和ω2，小球受力情况如图所示．





对第一种情况，有


eq \b\lc\{\rc\ (\a\vs4\al\c1(FT1cs30°＝mg，,FT1sin30°＝mlsin30°ω\\al(2,1)，))


可得ω1＝2.4 rad/s.


对第二种情况，有


eq \b\lc\{\rc\ (\a\vs4\al\c1(FT2cs45°＝mg，,FT2sin45°＝mlsin30°ω\\al(2,2)，))


可得ω2＝3.16 rad/s.


所以要使两绳始终张紧，ω必须满足的条件是：


2．4 rad/s≤ω≤3.16 rad/s.


答案 2.4 rad/s≤ω≤3.16 rad/s