浙教版八年级下册4.3 中心对称精品练习

这是一份浙教版八年级下册4.3 中心对称精品练习，共8页。试卷主要包含了3《中心对称》，如图所示，该图案是经过，求CD的长．等内容，欢迎下载使用。
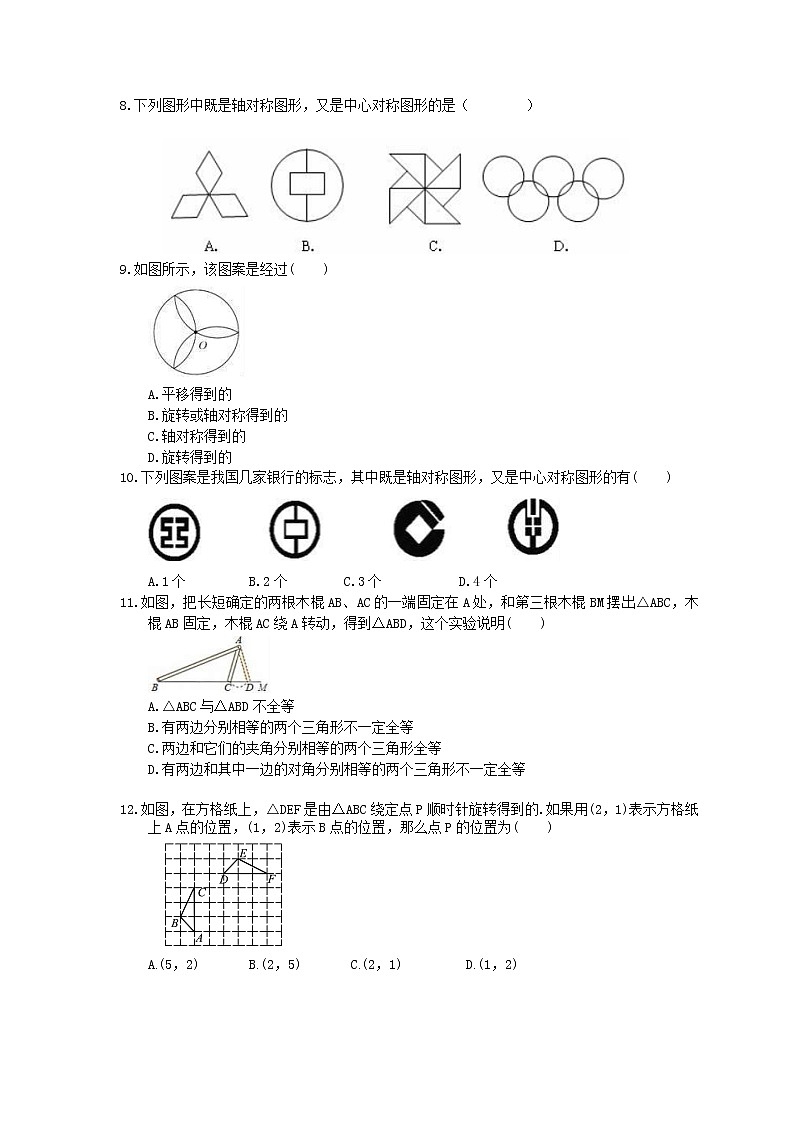
浙教版数学八年级下册4.3《中心对称》精选练习一、选择题1.在下列图形中，既是轴对称图形又是中心对称图形的是                  （ ） 2.下列四个图案中，是中心对称图形的是(　　)A．   B．    C．    D． 3.下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是(　　)A.  B.   C.   D.4.下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（  ）5.下列图形中，你认为既是中心对称图形又是轴对称图形的是（        ）   6.由图所示的地板砖各两块所铺成的下列图案中,既是轴对称图形,又是中心对称图形的是（   ）      A.              B.              C.              D.7.下列四个图形中，不是中心对称图形的是(       )A．                   B．                  C．                   D．8.下列图形中既是轴对称图形，又是中心对称图形的是（        ）  9.如图所示，该图案是经过(    )A.平移得到的B.旋转或轴对称得到的C.轴对称得到的D.旋转得到的10.下列图案是我国几家银行的标志，其中既是轴对称图形，又是中心对称图形的有(　　)A.1个                       B.2个                      C.3个                         D.4个11.如图，把长短确定的两根木棍AB、AC的一端固定在A处，和第三根木棍BM摆出△ABC，木棍AB固定，木棍AC绕A转动，得到△ABD，这个实验说明(　　)A.△ABC与△ABD不全等              B.有两边分别相等的两个三角形不一定全等              C.两边和它们的夹角分别相等的两个三角形全等              D.有两边和其中一边的对角分别相等的两个三角形不一定全等 12.如图，在方格纸上，△DEF是由△ABC绕定点P顺时针旋转得到的.如果用(2，1)表示方格纸上A点的位置，(1，2)表示B点的位置，那么点P的位置为(    )A.(5，2)       B.(2，5)       C.(2，1)         D.(1，2)   二、填空题13.在平面直角坐标系中，若点P(x－2，x)关于原点的对称点在第四象限，则x的取值范围是________．14.如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′(点B′与点B是对应点，点C′与点C是对应点)，点B′恰好落在BC边上，则∠C=     度. 15.如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是           ．16.如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为，则图中阴影部分的面积是 ______ ．17.在平面直角坐标系中，设点P到原点的距离为ρ(希腊字母读作“柔”)，OP看作由x轴的正半轴逆时针旋转而成的夹角α，则用[ρ，α]表示点P的雷达坐标，则点P(﹣7，7)的雷达坐标为　   　.18.如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA=6，PB=8，PC=10，则四边形APBQ的面积为　　     ．三、作图题19.如图所示，已知点O是四边形ABCD的边DC的中点，请你作出四边形ABCD关于点O成中心对称的四边形.    四、解答题20.如图，将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，AB与A1C1相交于点D，AC与A1C1、BC1分别交于点E、F.(1)求证：△BCF≌△BA1D.(2)当∠C=α度时，判定四边形A1BCE的形状并说明理由.           21.如图，△AEC绕A点顺时针旋转60°得△APB，∠PAC=20°，求∠BAE.     22.如图，在△ABC中，∠C=90°，AC=2cm，AB=3cm，将△ABC绕点B顺时针旋转60°得到△FBE，求点E与点C之间的距离.       23.如图，在四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．线段CD绕点C顺时针旋转60°得到线段CE，连接AE.(1)求证：AE=BD；(2)若∠ADC=30°，AD=3，BD=4.求CD的长．       24.问题发现：如图1，△ABC是等边三角形，点D是边AD上的一点，过点D作DE∥AC交AC于E，则线段BD与CE有何数量关系？拓展探究：如图2，将△ADE绕点A逆时针旋转角α（0°＜α＜360°），上面的结论是否仍然成立？如果成立，请就图中给出的情况加以证明．问题解决：如果△ABC的边长等于2，AD=2，直接写出当△ADE旋转到DE与AC所在的直线垂直时BD的长． 
参考答案1.C2.答案为：A.3.B.4.答案为：B5.A6.A7.C8.B9.答案为：B  10.B.11.答案为：D.12.答案为：A；13.答案为：0＜x＜2　14.答案为：10515.答案为：（﹣4，3）．16.答案为：   17.答案为：[7，135°]. 18.答案为：24+9．19.解：如图所示，连接AO并延长AO到A1，使OA1=AO，连接BO并延长BO到B1，使OB1=BO，连接CA1，A1,B1，B1D，则四边形A1B1DC就是所求作的四边形.20.(1)证明：∵△ABC是等腰三角形，∴AB=BC，∠A=∠C，∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，∴A1B=AB=BC，∠A=∠A1=∠C，∠A1BD=∠CBC1，在△BCF与△BA1D中，，∴△BCF≌△BA1D；(2)解：四边形A1BCE是菱形，∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，∴∠A1=∠A，∵∠ADE=∠A1DB，∴∠AED=∠A1BD=α，∴∠DEC=180°﹣α，∵∠C=α，∴∠A1=α，∴∠A1BC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α，∴∠A1=∠C，∠A1BC=∠A1EC，∴四边形A1BCE是平行四边形，∴A1B=BC，∴四边形A1BCE是菱形.21.解：根据旋转的性质可得△ABP≌△ACE，AC与AB是对应边，∠BAC=∠BAP+∠PAC=60°，∵∠PAC=20°，∴∠CAE=∠BAP=40°，∴∠BAE=∠BAC+∠CAE=100°.22.解：连接EC，即线段EC的长是点E与点C之间的距离，在Rt△ACB中，由勾股定理得：BC===将△ABC绕点B顺时针旋转60°得到△FBE，∴BC=BE，∠CBE=60°∴△BEC是等边三角形∴EC=BE=BC= 23.解：(1)易证△ACE≌△BCD(SAS)，∴AE=BD.(2)连接DE.∵CD=CE，∠DCE=60°，∴△DCE是等边三角形．∴∠CDE=60°，DC=DE.∵∠ADC=30°，∴∠ADC＋∠CDE=90°.∵AD=3，BD=4，∴AE=BD=4.∴DE=.∴DC=DE=.24.