


人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.1 平行线的性质一等奖ppt课件
展开∵∠2+∠4=180°
方法4:如图1,若a∥b,b∥c,则a∥c.( ) 方法5:如图2,若a⊥b,a⊥c,则b∥c.( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
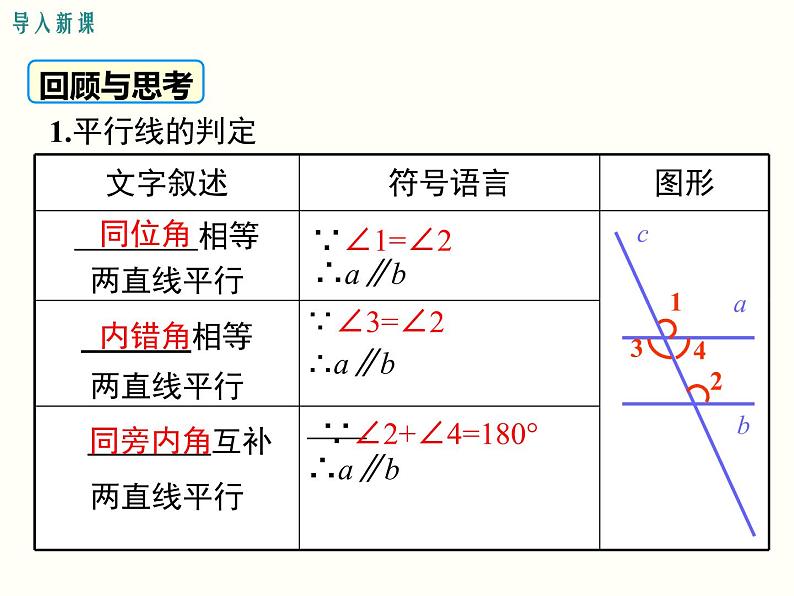
2.平行线的其它判定方法
∠2+∠4=180 °
例1:如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°. (1)DE和BC平行吗?为什么?(2)∠C是多少度?为什么?
解:(1) DE∥BC.理由如下: ∵ ∠ADE=60°,∠B = 60° ∴ ∠ADE=∠B ∴ DE∥BC (同位角相等,两直线平行 ).
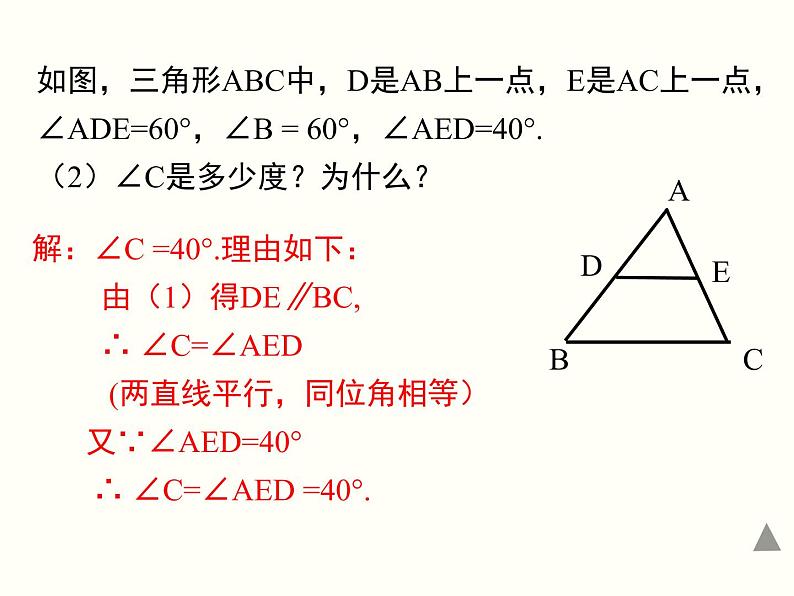
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°. (2)∠C是多少度?为什么?
解:∠C =40°.理由如下: 由(1)得DE∥BC, ∴ ∠C=∠AED (两直线平行,同位角相等) 又∵∠AED=40° ∴ ∠C=∠AED =40°.
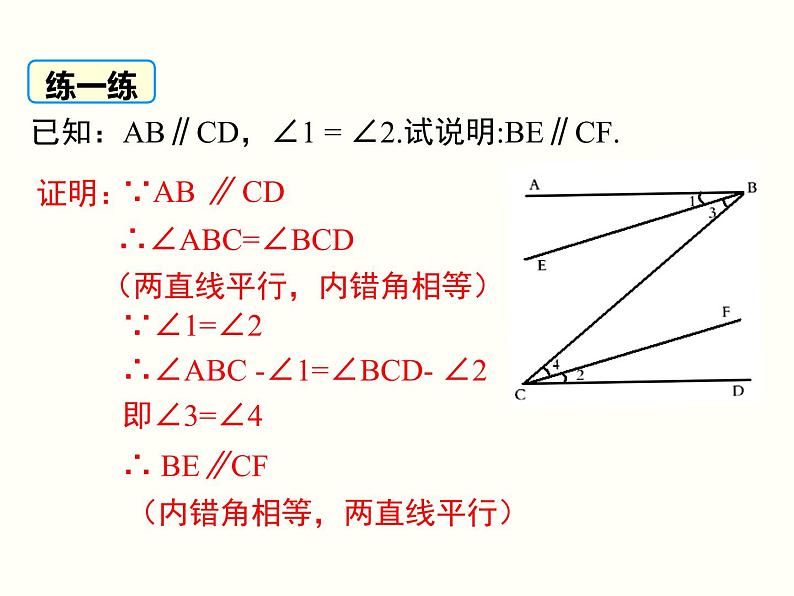
已知:AB∥CD,∠1 = ∠2.试说明:BE∥CF.
(两直线平行,内错角相等)
∴∠ABC -∠1=∠BCD- ∠2
(内错角相等,两直线平行)
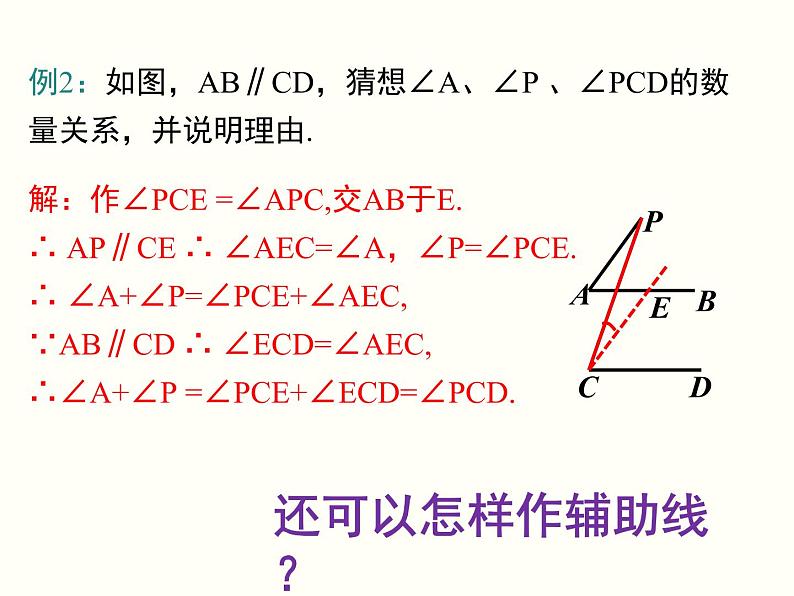
例2:如图,AB∥CD,猜想∠A、∠P 、∠PCD的数量关系,并说明理由.
解:作∠PCE =∠APC,交AB于E.∴ AP∥CE ∴ ∠AEC=∠A,∠P=∠PCE.∴ ∠A+∠P=∠PCE+∠AEC,∵AB∥CD ∴ ∠ECD=∠AEC,∴∠A+∠P =∠PCE+∠ECD=∠PCD.
例2:如图,AB∥CD,猜想∠BAP、∠APC 、∠PCD的数量关系,并说明理由.
解法2:作∠APE =∠BAP.∴ EP∥AB,∵AB∥CD ∴ EP∥CD,∴∠EPC=∠PCD∴ ∠APE+∠APC= ∠PCD即∠BAP+∠APC =∠PCD.
例3:如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
解:过点E 作EF//AB. ∴∠B=∠BEF. ∵AB//CD. ∴EF//CD. ∴∠D =∠DEF. ∴∠B+∠D=∠BEF+∠DEF =∠DEB. 即∠B+∠D=∠DEB.
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
解:过点E 作EF//AB. ∴∠B+∠BEF=180°. ∵AB//CD. ∴EF//CD. ∴∠D +∠DEF=180°. ∴∠B+∠D+∠DEB =∠B+∠D+∠BEF+∠DEF =360°. 即∠B+∠D+∠DEB=360°.
变式2:如图,AB∥CD,则 :
若有n个拐点,你能找到规律吗?
变式3:如图,若AB∥CD, 则:
若左边有n个角,右边有m个角;你能找到规律吗?
(1)∠1= 时,AB∥CD.
(2)∠3= 时,AD∥BC.
2.直线a,b与直线c相交,给出下列条件: ①∠1= ∠2; ②∠3= ∠6; ③∠4+∠7=180; ④∠3+ ∠5=180°,其中能判断a//b的是( )A. ①②③④ B .①③④ C. ①③ D. ④
3. 有这样一道题:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数. 请补全下列解答过程
解:过点E作EF//AB.∵AB//CD(已知),∴ // (平行于同一直线的两直线平行).∴∠A+∠ =180,∠C+∠ =180(两直线平行,同旁内角互补).又∵∠A=100°,∠C=110°(已知), ∴∠ = °, ∠ = °.∴∠AEC=∠1+∠2= °+ ° = °.
4.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
(内错角相等,两直线平行).
∵AB⊥BF,CD⊥BF,
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
5.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD 的度数.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(两直线平行,同旁内角互补)
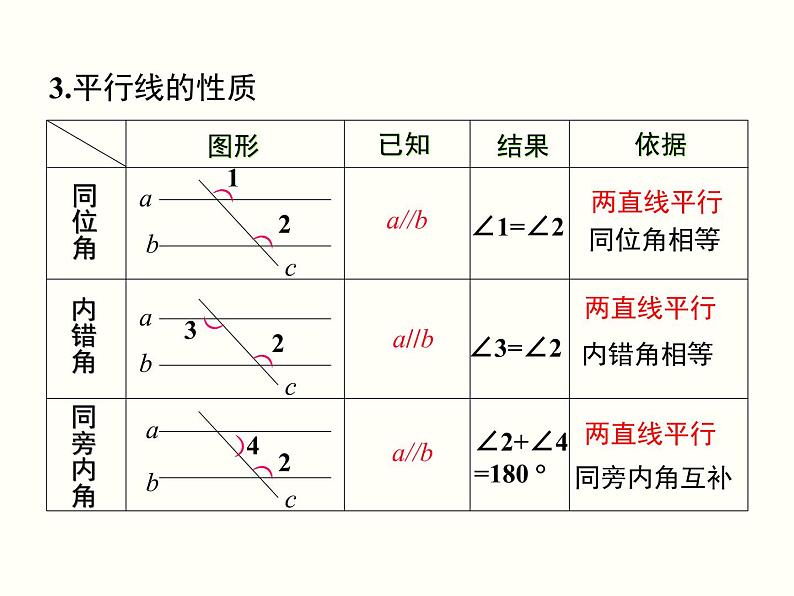
初中数学人教版七年级下册5.3.1 平行线的性质教学演示课件ppt: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c88546_t3/?tag_id=26" target="_blank">5.3.1 平行线的性质教学演示课件ppt</a>,共13页。PPT课件主要包含了学习目标,同位角,内错角,同旁内角,∵∠1∠2,∠3∠2,平行线的判定,自主学习,两直线平行,同位角相等等内容,欢迎下载使用。
人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.1 平行线的性质公开课课件ppt: 这是一份人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.1 平行线的性质公开课课件ppt,共21页。PPT课件主要包含了3平行线的性质,内错角,同位角,两条直线平行,同旁内角,角之间的关系,∠1∠2,AB∥EF,CD⊥BF,AB∥CD等内容,欢迎下载使用。
人教版七年级下册5.3.1 平行线的性质优秀课件ppt: 这是一份人教版七年级下册5.3.1 平行线的性质优秀课件ppt,共18页。PPT课件主要包含了角的数量关系,证明AD∥EF,角之间的关系,∵AB∥CD,∴∠ABC∠BCD,∵∠1∠2,即∠3∠4,∴BE∥CF,∴EF∥CD,过点E作EF∥AB等内容,欢迎下载使用。













