人教版八年级下册18.2.1 矩形一等奖ppt课件

这是一份人教版八年级下册18.2.1 矩形一等奖ppt课件，共21页。PPT课件主要包含了温故知新，一个角是直角，两组对边分别平行，情景创设，矩形的定义，∴ACBD，矩形的性质，矩形对边平行且相等，相等的角，试一试等内容，欢迎下载使用。

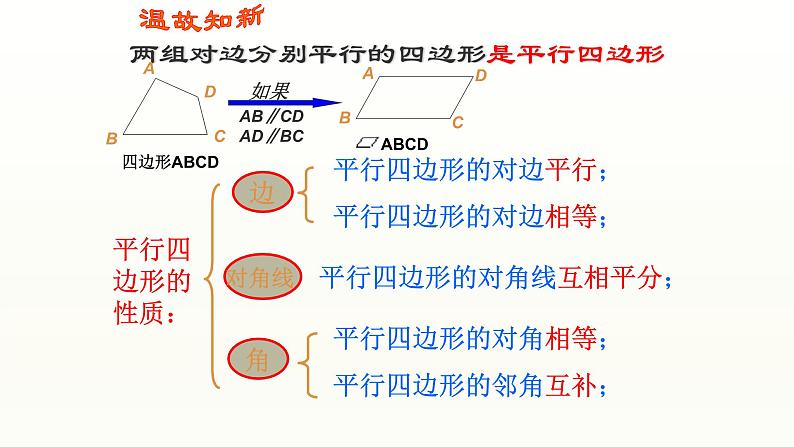
两组对边分别平行的四边形是平行四边形
平行四边形的对边平行；
平行四边形的对边相等；
平行四边形的对角相等；
平行四边形的邻角互补；
平行四边形的对角线互相平分；
两组对边分别平行的四边形；
两组对边分别相等的四边形；
两组对角分别相等的四边形；
对角线互相平分的四边形；
一组对边平行且相等的四边形；
平行四边形的判定定理：
定义：把连接三角形两边中点的线段叫做三角形的中位线
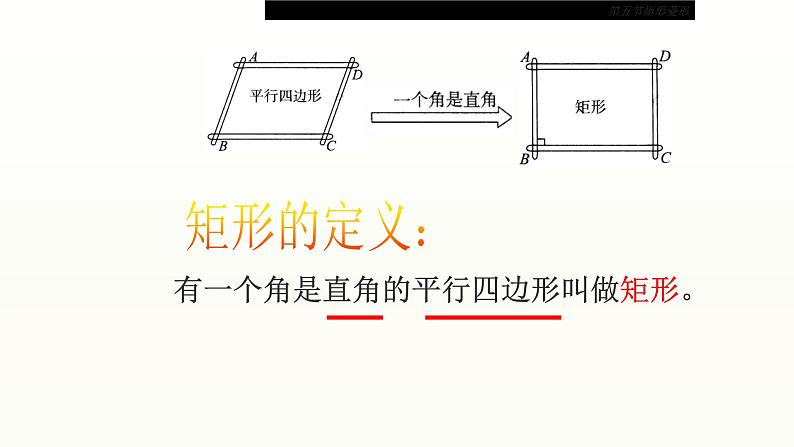
我们已经知道平行四边形是特殊的四边形，因此平行四边形除具有四边形的性质外，还有它的特殊性质，同样对于平行四边形来说有特殊情况即特殊的平行四边形，也，这堂课我们就来研究一种恃殊的平行四边形——
有一个角是直角的平行四边形叫做矩形。
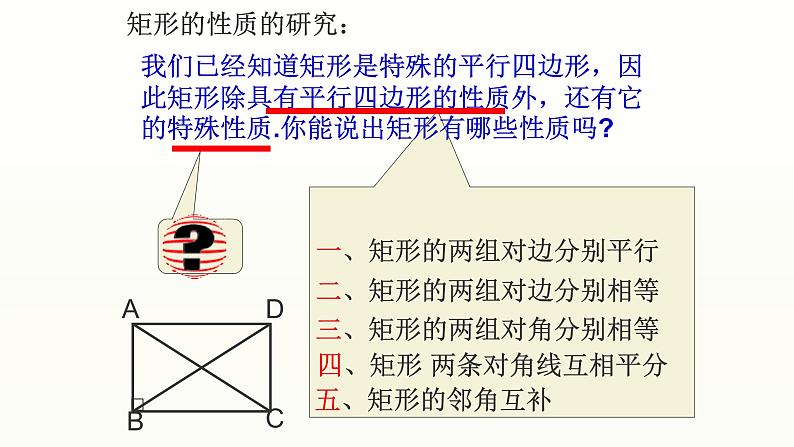
我们已经知道矩形是特殊的平行四边形，因此矩形除具有平行四边形的性质外，还有它的特殊性质.你能说出矩形有哪些性质吗?
四、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
命题1:矩形的四个角都是直角；
已知：四边形ABCD是矩形求证：∠A=∠B=∠C=∠D=90°
证明：∵四边形ABCD是平行四边形， ∠C=90° ∴∠A=∠C=90° ∠B+∠C=180 ° ∴∠B=180－∠C=90° ∴∠D=∠B=90° 即∠A=∠B=∠C=∠D=90°
已知：四边形ABCD是矩形 求证：AC = BD
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
∴△ABC≌△DCB（SAS）
命题2:矩形的对角线相等；
矩形的四个角都是直角；
矩形的对角线相等且平分；
直角三角形性质定理：直角三角形斜边上的中线等于斜边的一半．
如图，矩形ABCD中，对角线AC、BD相交于点O，请探讨OC与BD的关系
推论：直角三角形斜边上的中线等于斜边的一半.
证明：延长CD到E使DE=CD，连结AE、BE.
∵AD = BD ， DE =CD∴四边形ACBE是平行四边形
∠DAB=∠ABC=∠BCD=∠CDA=90° ∠AOB=∠DOC ∠AOD=∠BOC∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
△OAB △ OBC △OCD △OAD
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
思考：矩形ABCD是轴对称图形吗？
矩形是中心对称图形吗？对称中心是？
例1： 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°,AB=4㎝,求矩形对角线的长？
解：∵四边形ABCD是矩形 ∴ OA=OB ∵∠AOB=60° ∴△AOB是等边三角形 ∴OA=AB=4(㎝) ∴矩形的对角线长 AC=BD=2OA=8(㎝)
例2：如图，△ABC中，∠ACB=900，点D、E分别为AC、AB的中点，点F在BC延长线上，且∠CDF=∠A，求证：四边形DECF是平行四边形；
四边形ABCD是矩形若已知AB=8㎝，AD=6㎝， 则AC＝ ㎝ OB= ㎝若已知∠CAB=40°，则∠OCB= ∠OBA= ∠AOB= ∠AOD= 若已知AC＝10㎝，BC=6㎝，则矩形的周长＝ ㎝ 矩形的面积＝ ㎝24 若已知 ∠DOC=120°，AD＝6㎝，则AC= ㎝
已知△ABC是Rt△，∠ABC=Rt∠，BD是斜边AC上的中线
若BD=3㎝则AC＝ ㎝2 若∠C=30°，AB＝5㎝，则AC＝ ㎝， BD＝ ㎝，∠BDC＝
练一练：书本P104：练习3
练习：如图四边形ABCD中，∠ABC=∠ADC=900，E是AC中点，EF平分∠BED交BD于点F，（1）猜想EF与BD具有怎样的关系？（2）试证明你的猜想。
如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm，对角线的长是13cm，那么矩形的周长是多少？