初中数学人教版八年级下册19.2.3一次函数与方程、不等式优质课ppt课件

这是一份初中数学人教版八年级下册19.2.3一次函数与方程、不等式优质课ppt课件，共20页。PPT课件主要包含了复习回顾，探究新知，动手操作，数形结合分析，ax+b0的解，ax+bt的解，x-2，ax+b0的解集，ax+bt的解集，针对性练习等内容，欢迎下载使用。

学习目标：　1．认识一次函数与一元一次方程、一元一次不等式之间的联系．会用函数观点解释方程和不等式及其解(解集)的意义；　2．经历用函数图象表示方程、不等式解的过程，进一步体会“以形表数，以数释形”的数形结合思想．学习重点：　 理解一次函数与一次方程、一次不等式的关系；
【活动1】我们学习了平面直角坐标系，请同学们回顾下：对于点P（x,y），当y=0,y>0,y<0时，点P位于坐标平面内什么位置？
【活动2】请同学们快速解下面3个方程！
【思考】(1)上面三个方程有什么共同点和不同点？(2)你能从函数的角度对解这3个方程进行解释吗？
请画出一次函数y=2x+6的图象
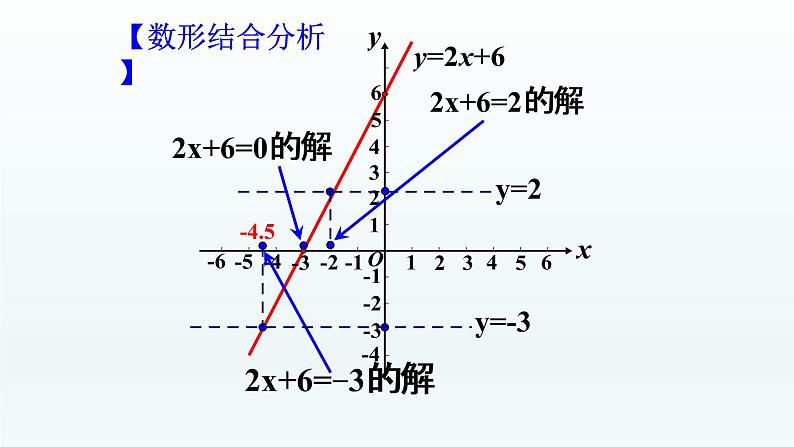
【观察-思考-讨论】观察图象回答下列问题：
问题1：在图象上怎么找函数值y=0对应的点？如何读出该点的横坐标x的值是多少？该点横坐标的值与一元一次方程2x+6=0的解有何关系？
问题2：类比问题1，如何找y=-3或2时对应点的位置？读出该点的横坐标x的值，它与一元一次方程2x+6=-3或2的解有何关系？
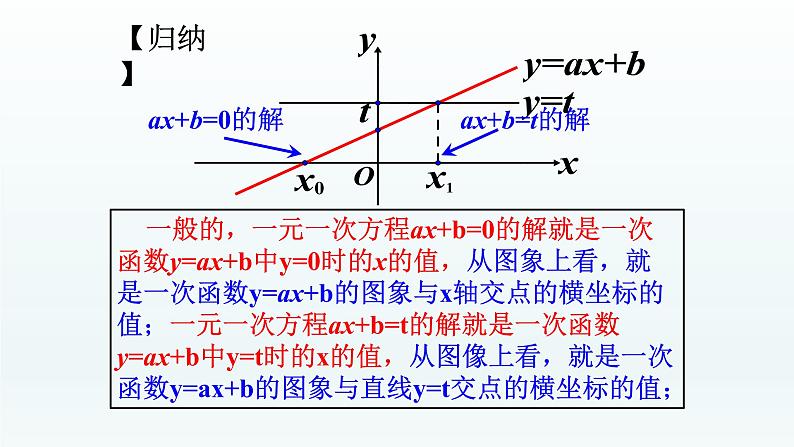
一般的，一元一次方程ax+b=0的解就是一次函数y=ax+b中y=0时的x的值，从图象上看，就是一次函数y=ax+b的图象与x轴交点的横坐标的值；一元一次方程ax+b=t的解就是一次函数y=ax+b中y=t时的x的值，从图像上看，就是一次函数y=ax+b的图象与直线y=t交点的横坐标的值；
针对性练习：1.已知一次函数y=0.5x-2与x轴交点为(4,0),那么方程0.5x-2=0的解是 .2.已知一次函数y=kx-b与x轴交点为(-2,0)，那么方程kx-b=0的解是 .3.已知方程kx+b=0的解是x=3，那么一次函数y=kx+b与x轴交点为 .
【活动3】请同学们快速解下列不等式的解集！
【思考】(1)上面三个不等式有什么共同点和不同点？(2)你能从函数的角度对解这3个不等式进行解释吗？
【观察-思考-讨论】观察图象回答下列问题
问题2：根据图象，你能说出函数值y<0时自变量x的取值范围吗？它与不等式2x+6<0的解集相同吗？
问题3：根据图象，如何找函数值y>2时自变量的取值范围？你找出来的自变量的范围与2x+6>2的解集是否相同？
问题1：根据图象，你能说出函数值y>0时自变量x的取值范围吗？它与不等式2x+6>0的解集相同吗？
从图象上看ax+b>0的解集是使直线y=ax+b位于x轴上方相应x的取值范围； ax+b<0的解集是使直线y=ax+b位于x轴下方相应x的取值范围。
不等式ax+b>t的解集等价于直线y=ax+b在直线y=t上方的部分对应的x的取值范围；不等式ax+b 1.一次函数y=-x+2的图象如图，你能说出-x+2<0的解集么？
2.一次函数y=kx+b的图象如图所示，你能说出关于x的不等式kx+b<0的解集么？
3.根据函数y=-3x+6的图象，回答问题：（1）求方程-3x+6=0的解;（2）求不等式-3x+6>0 和 -3x+6<0的解集;（3）当x取何值时，0(1)x=2(2)x<2;x>2(3)1（1）请用函数的观点，说说你对一元一次方程有什么新的认识；（2）请用函数的观点，说说一次函数与一元一次不等式的联系．
1.一次函数y=ax+b的图象如图所示，则方程ax+b=0的解是( )
A、x=-2 B、x=0C、x=-1 D、x=-3
2.一次函数y=ax+b的图象如图所示，则方程ax+b=2的解是( )
A、x=2 B、x=-2C、x=1 D、x=-1
3.一次函数y=ax+b的图像如图所示，则不等式ax+b≥0的解集是( )
A、x≥2 B、x≤2C、x≥4 D、x≤4
4.一次函数y=ax+b的图像如图所示，则0≤ax+b＜3的解集是( )
A、0≤x<3 B、0≤x<1 C、-2≤x<1 D、-2≤x<3
5.如图，已知直线y=kx-b,则关于x的方程kx-1=b的解是 .
6.已知关于x的方程ax-b=1的解是x=-1，则一次函数y=ax-b-1的图像与x轴交点的坐标是 .