人教版八年级下册第十七章 勾股定理17.1 勾股定理精品课件ppt

这是一份人教版八年级下册第十七章 勾股定理17.1 勾股定理精品课件ppt，共33页。PPT课件主要包含了看谁算得快，S5S1+S24，S6S3+S46，“勾股树”，知识回顾，变式训练1，变式训练2，勾股定理的内容，数学海螺图，例题分析等内容，欢迎下载使用。

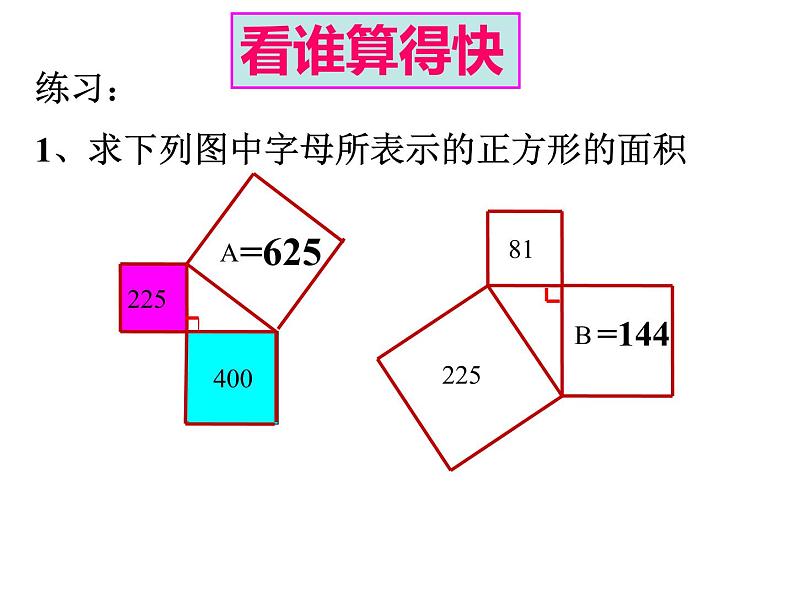
练习：1、求下列图中字母所表示的正方形的面积
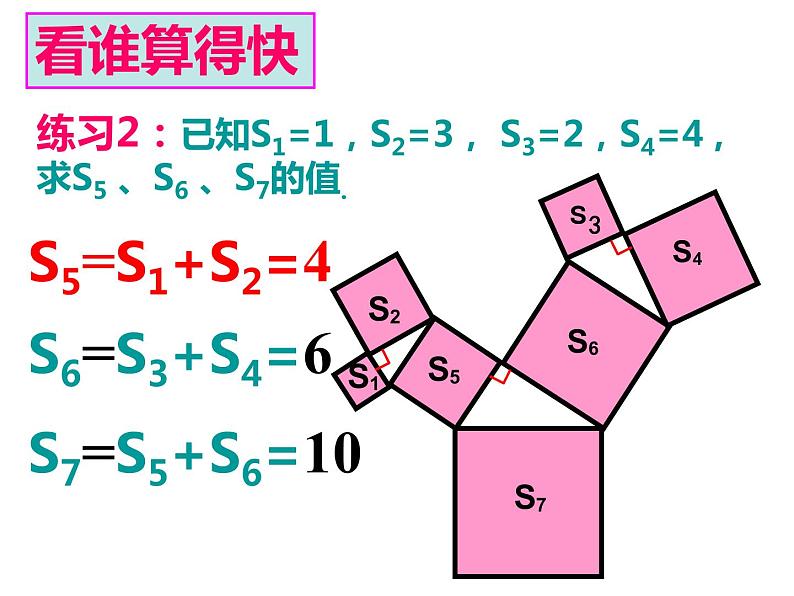
练习2：已知S1=1，S2=3， S3=2，S4=4 , 求S5 、S6 、S7的值.
S7=S5+S6=10
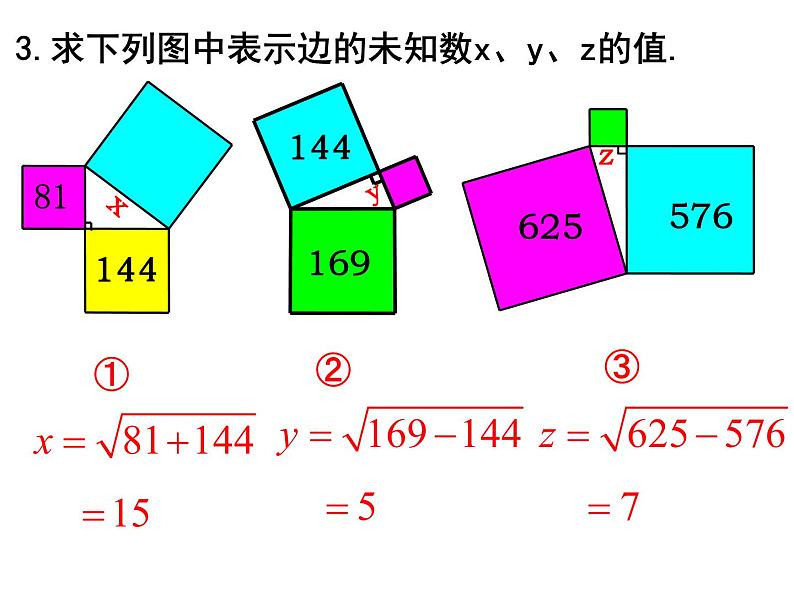
3.求下列图中表示边的未知数x、y、z的值.
勾股定理及其数学语言表达式:
直角三角形两直角边的平方和等于斜边的平方。
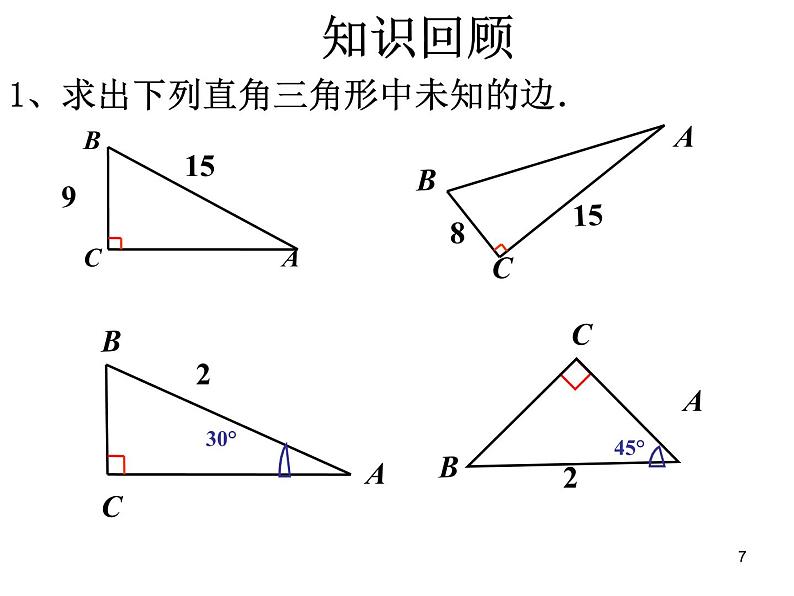
1、求出下列直角三角形中未知的边．
2、在直角三角形中,如果有两边 为3，4，那么另一边为________。
3. 台风袭击中，一棵大树在离地面9米处断裂，树的顶部落在离树根底部12米处。这棵树原来有多高？
一个门框的尺寸如图所示，一块长3m，宽2.2m的薄木板能否从门框内通过?为什么?
解：连结AC,在Rt△ABC中,根据勾股定理,因此,AC= ≈2.236因为AC______木板的宽,所以木板____ 从门框内通过.
一种盛饮料的圆柱形杯（如图），测得内部底面直径为5㎝，高为12㎝，吸管放进杯里，杯口外面露出5㎝，问吸管要做多长？
做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明。
一个2.6m长的梯子AB，斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
3.两点之间　　　最短。
2、把直角三角形两条直角边同时扩大到原来的3倍，则其斜边（ ） A.不变 B.扩大到原来的3倍 C.扩大到原来的9倍 D.减小到原来的1/3
例1：有一个圆柱,它的高等于12厘米，底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁，它想从点A爬到点B ， 蚂蚁沿着圆柱侧面爬行的最短路程是多少？(π的值取3)
长18cm (π的值取3)
∵ AB2=92+122=81+144=225=
∴ AB=15(cm)
蚂蚁爬行的最短路程是15厘米.
◆在长30cm、宽50 cm、高40 cm的木箱中，如果在箱内的A处有一只昆虫，它要在箱壁上爬行到B处，至少要爬多远？
例： 如图，边长为1的正方体中，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是（ 　）. （A）3 （B ) （C）2 （D）1
2.如图是6级台阶侧面的示意图，如果要在台阶上铺地毯，那么至少要买地毯多少米？
如图，是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点的最短路程是_________
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B，使AB=2;
你能在数轴上表示出 的点吗？
在数学中也有这样一幅美丽的“海螺型”图案
由此可知,利用勾股定理,可以作出长为
第七届国际数学教育大会的会徽
1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段?
8.一架5长的梯子，斜立靠在一竖直的墙上，这是梯子下端距离墙的底端3，若梯子顶端下滑了1,则梯子底端将外移（ ）9.如图，要在高3m,斜坡5m的楼梯表面铺地毯，地毯的长度至少需（ ）米10.把直角三角形两条直角边同时扩大到原来的3倍，则其斜边（ ）A.不变 B.扩大到原来的3倍C.扩大到原来的9倍 D.减小到原来的1/3
例：已知:如图,等边△ABC的边长是 6 . (1)求高AD的长; (2)求S△ABC .