初中人教版19.2.3一次函数与方程、不等式获奖课件ppt

这是一份初中人教版19.2.3一次函数与方程、不等式获奖课件ppt，共24页。PPT课件主要包含了知识回顾，解下列一元一次方程，13x+10，25y-23，解∵3x+10，∴3x-1，解∵5y-23，∴5y5，解得y1，解得x4等内容，欢迎下载使用。

（4）3(y-2) +1=2y
∴2(2x+1)-3x=6，即4x-3x=6-2
解：∵3(y-2) +1=2y
∴3y-6+1=2y，即3y-2y=6-1
1.理解一次函数与一元一次方程的关系.2.会根据一次函数图象求解一元一次方程.
下面 3 个方程有什么共同点和不同点？
(1) 2x+1=3；(2) 2x+1=0；(3) 2x+1=-1.
你能从函数的角度对解这 3 个方程进行解释吗？
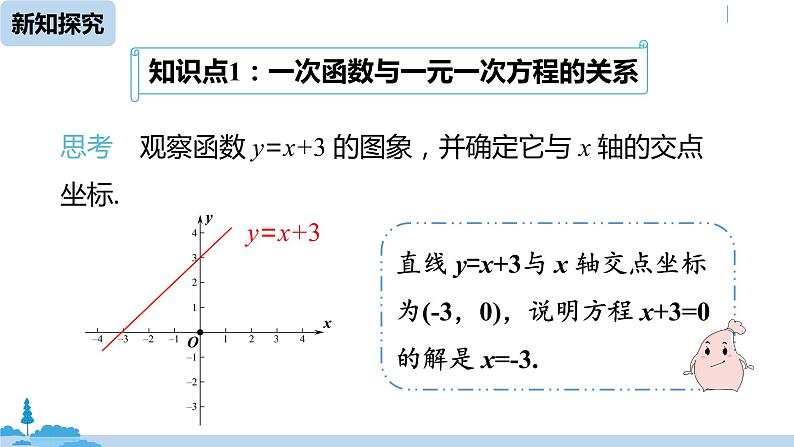
思考 观察函数 y=x+3 的图象，并确定它与 x 轴的交点坐标.
函数 y=kx+b（k≠0）中，当 y=0时，x 的值.
方程 kx+b=0（k≠0）的解.
函数 y=kx+b（k≠0）的图象与 x 轴交点的横坐标.
方程kx+b=0（k≠0）的解.
思考 观察下列函数图象，你能说出一元一次方程的解吗？
一元一次方程-x-2=0的解为 x=-2.
一元一次方程2x-2=0的解为 x=1.
利用一次函数的图象解一元一次方程的步骤：
（1）转化：将一元一次方程转化为一次函数；
（2）画图象：画出一次函数的图象；
（3）找交点：找出一次函数图象与 x 轴的交点，则交点的横坐标即一元一次方程的解.
1.已知一元一次方程 ax+b=0 的解为 x=4，则一次函数 y=ax+b的图象与 x 轴的交点坐标为 .
解：∵ 一元一次方程 ax+b=0 的解为 x=4
∴ 当 x=4 时，一次函数 y=ax+b 的函数值为 0
∴ 一次函数图象与 x 轴的交点坐标为（4，0）
2.已知一次函数 y=kx+b 的图象与 x 轴的交点坐标为（-3，0），一元一次方程 kx+b=0 的解为 .
解：∵ 一次函数 y=kx+b 的图象与 x 轴的交点坐标为（-3，0）
∴ 当 x=-3 时，一次函数 y=kx+b 的函数值为0，也即 kx+b=0 的解.
1.若一次函数 y=kx+b 的图象经过点（2，0）和（0，-3），则方程 kx+b=0 的解为（ ）.
A. x=0 B. x=2 C. x=-3 D. 不能确定
2.一次函数 y=kx+b 的图象如图所示，则方程 kx+b=0 的解为 ，方程 kx+b=2 的解为 .
解析：∵直线 y=kx+b 与 x 轴的交点坐标是(-1，0)，与 y 轴的交点坐标为(0，2)，即当y=0 时，x=-1；当 y=2 时，x=0.
∴方程 kx+b=0 的解是 x=-1，方程 kx+b=2 的解是 x=0.
3.利用图象法解方程 6x-3 = x+2.
解：将方程 6x-3=x+2 变形为 5x-5=0，
画出函数 y=5x-5 的图象.
由图象可知：直线 y=5x-5 与 x 轴的交点为（1，0）
即 x=1 是方程的解.
一次函数与一元一次方程
①从“数”上看；②从“形”上看.
①转化；②画图象；③找交点.
1.一次函数 y=kx+b 的图象如图所示，则方程 kx+b=1 的解为（ ）.
2.如图，已知直线 y=kx+b，求关于 x 的方程 kx-2=-b 的解.
解：由图可知：一次函数 y=kx+b 经过点（1，2），也即当 x=1时，kx+b=2.
因为关于 x 的方程 kx-2=-b 可以化简为 kx+b=2，所以方程的解为 x=1.
3.已知一个机器的运行速度为 3 转/s，每过 1s 其运行的速度增加 2 转，试问再过多少秒它的速度能到 23 转/s？
解：设再过 x 秒机器的速度能达到 23 转/s
由题意可得：3+2x=23
所以再过 10s 它的速度能达到 23 转/s.