



2020---2021学年北师大版七年级数学下册 期末综合测试卷
展开一、选择题(本大题共10小题,每小题3分,共30分)
1.(2020·遵义)下列计算正确的是( C )
A.x2+x=x3
B.(-3x)2=6x2
C.8x4÷2x2=4x2
D.(x-2y)(x+2y)=x2-2y2
2.(2019秋·中山市期末)下列事件中,属于必然事件的是( C )
A.任意购买一张电影票,座位号是奇数
B.明天晚上会看到太阳
C.五个人分成四组,这四组中有一组必有2人
D.三天内一定会下雨
3.如图,直线l是一条河,A,B是两个新农村定居点.欲在l上的某点处修建一个水泵站,由水泵站直接向A,B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( D )
4.(2020·揭西县模拟)下列图形中:①等腰梯形;②等边三角形;③平形四边形;④圆,一定是轴对称图形而且对称轴不止一条的有( B )
A.1个 B.2个
C.3个 D.4个
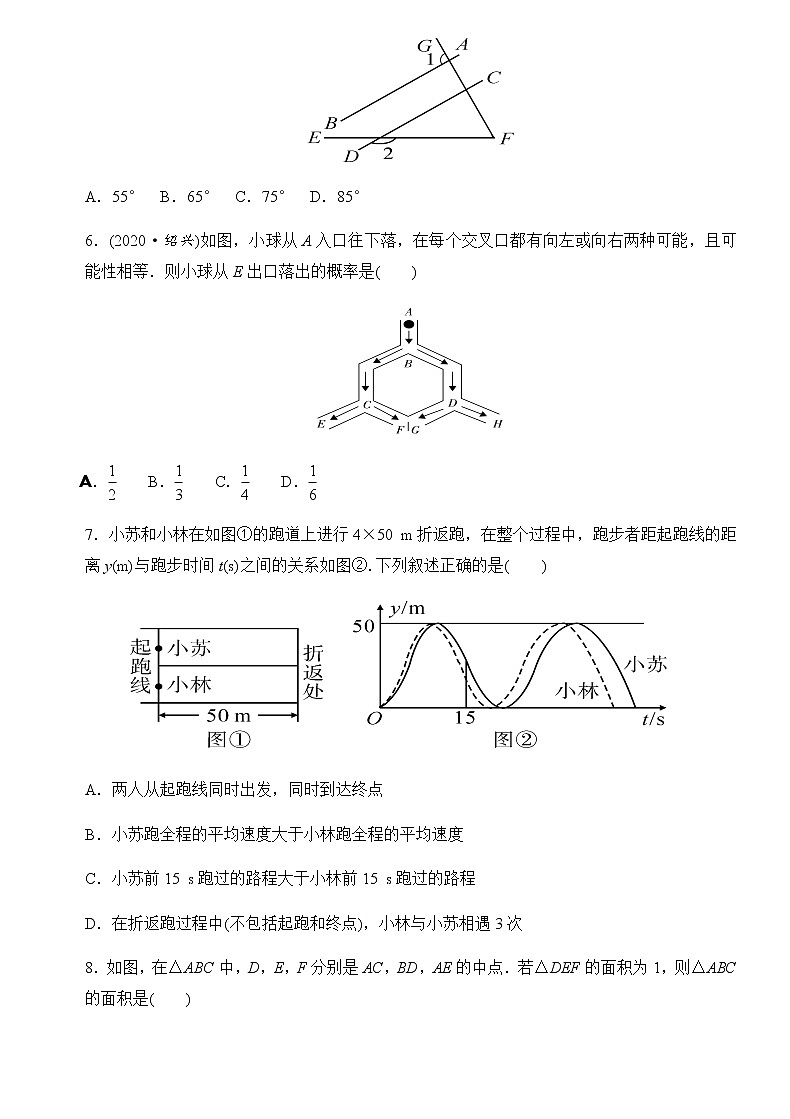
5.如图,已知AB∥CD,∠1=100°,∠2=145°,那么∠F=( B )
A.55° B.65° C.75° D.85°
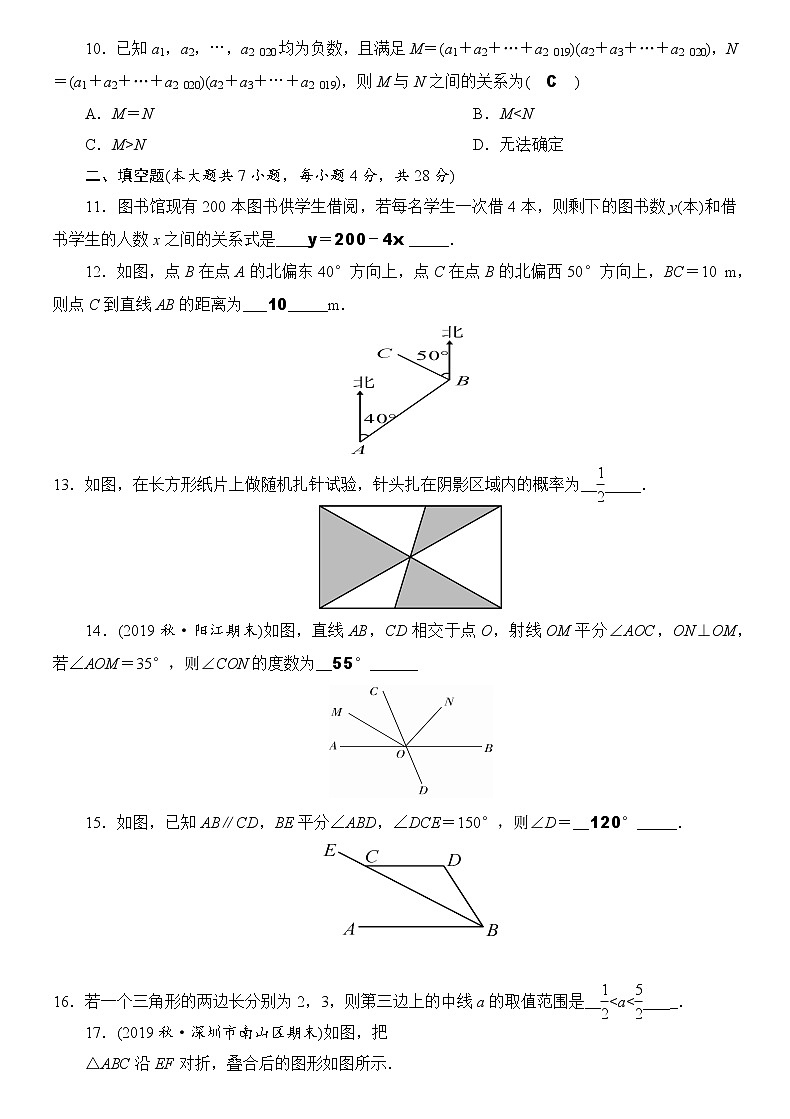
6.(2020·绍兴)如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球从E出口落出的概率是( C )
eq \f(1,2) B.eq \f(1,3) C.eq \f(1,4) D.eq \f(1,6)
7.小苏和小林在如图①的跑道上进行4×50 m折返跑,在整个过程中,跑步者距起跑线的距离y(m)与跑步时间t(s)之间的关系如图②.下列叙述正确的是( D )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15 s跑过的路程大于小林前15 s跑过的路程
D.在折返跑过程中(不包括起跑和终点),小林与小苏相遇3次
8.如图,在△ABC中,D,E,F分别是AC,BD,AE的中点.若△DEF的面积为1,则△ABC的面积是( C )
A.3 B.4 C.8 D.12
9.(2019秋·佛山市南海区期末)如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,BC交于D,DE∥AB,交AC于E,则∠ADE的大小是( A )
A.40° B.45° C.50° D.54°
10.已知a1,a2,…,a2 020均为负数,且满足M=(a1+a2+…+a2 019)(a2+a3+…+a2 020),N=(a1+a2+…+a2 020)(a2+a3+…+a2 019),则M与N之间的关系为( C )
A.M=N B.M
C.M>N D.无法确定
二、填空题(本大题共7小题,每小题4分,共28分)
11.图书馆现有200本图书供学生借阅,若每名学生一次借4本,则剩下的图书数y(本)和借书学生的人数x之间的关系式是____y=200-4x _____.
12.如图,点B在点A的北偏东40°方向上,点C在点B的北偏西50°方向上,BC=10 m,则点C到直线AB的距离为___10_____m.
13.如图,在长方形纸片上做随机扎针试验,针头扎在阴影区域内的概率为__eq \f(1,2)____.
14.(2019秋·阳江期末)如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为__55°______
15.如图,已知AB∥CD,BE平分∠ABD,∠DCE=150°,则∠D=__120°_____.
16.若一个三角形的两边长分别为2,3,则第三边上的中线a的取值范围是__eq \f(1,2)
17.(2019秋·深圳市南山区期末)如图,把
△ABC沿EF对折,叠合后的图形如图所示.
若∠A=60°,∠1=85°,则∠2的度数为___35°_____.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.计算:(2x2)3-3x2·4x4+2x8÷x2.
解:原式=8x6-12x6+2x6=-2x6.
19.(2020·花都区一模)已知A=(x+2)2+(x+1)(x-1)-3.
(1)化简A;
(2)若x2=(eq \f(1,4))-1,求A的值.
解:(1)A=(x+2)2+(x+1)(x-1)-3=x2+4x+4+x2-1-3=2x2+4x;
(2):∵x2=(eq \f(1,4))-1=4,∴x=±2,
∴A=2x2+4x=2×4+4×2=8+8=16,或A=2x2+4x=2×4+4×(-2)=8-8=0,即A的值是0或16.
20.今年“五一”,小明外出爬山,他在从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用的时间为t(min),所走的路程为s(m),s与t之间的关系如图.
(1)小明中途休息用了___20_____min;
(2)小明在上述过程中所走的路程为__3800______m;
(3)分别求小明休息前、后爬山的平均速度.
解:由图象,得当t=40时,s=2 800,
所以小明休息前爬山的平均速度为2 800÷40=70(m/min).
小明休息后爬山的平均速度为
(3 800-2 800)÷(100-60)=25(m/min).
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥CD于点O,∠1=40°.求∠2和∠4的度数.
解:∵OF⊥CD,∴∠DOF=90°,
∴∠2=∠BOD=90°-∠1=50°.
∵OE平分∠AOD,
∴∠4=eq \f(1,2)∠AOD=eq \f(1,2)(180°-∠BOD)=65°.
22.如图,已知∠1+∠2=180°,∠3=∠B,则AB与DE平行吗?请说明理由.
解:AB∥DE.理由如下:
∵∠1+∠ADC=180°,∠1 +∠2=180°,
∴∠ADC=∠2,∴CD∥EF,∴∠3=∠CDE.
∵∠3=∠B,∴∠CDE=∠B,∴AB∥DE.
23.“五一”假期期间,某超市计划开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5或就中三等奖;指向其余数字不中奖.
(1)转动转盘中一等奖、二等奖、三等奖的概率是分别是多少?
(2)“五一”这天有1 800人参与这项活动,估计获得一等奖的人数是多少?
解:(1)由题意可知:P(一等奖)=eq \f(1,8); P(二等奖)=eq \f(1,4);P(三等奖)=eq \f(3,8);
:∵获得一等奖的概率是eq \f(1,8),∴“五一”这天有1 800人参与这项活动,估计获得一等奖的人数为1 800×eq \f(1,8)=225(人).
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,
∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△ABC和△ADE中,eq \b\lc\{(\a\vs4\al\c1(AB=AD,,∠BAC=∠DAE,,AC=AE,))
所以△ABC≌△ADE(SAS);
(2):∵∠CAE=90°,AC=AE,∴∠E=45°,
由(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CFA=90°,∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°;
(3):如答图,延长BF到G,使得FG=FB,
连接AG.
∵AF⊥BG,∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,eq \b\lc\{(\a\vs4\al\c1(BF=GF,,∠AFB=∠AFG,,AF=AF,))
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∵△ABC≌△ADE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,
∵∠GCA=∠DCA=45°,
在△CGA和△CDA中,eq \b\lc\{(\a\vs4\al\c1(∠GCA=∠DCA,,∠CGA=∠CDA,,AG=AD,))
∴△CGA≌△CDA(AAS),∴CG=CD,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数;
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
解:(1)∵AM∥BN,
∴∠ABN=180°-∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=eq \f(1,2)(∠ABP+∠PBN)=eq \f(1,2)∠ABN=60°;
(2):∵AM∥BN,∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,∴∠CBN=∠ABD,
∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=eq \f(1,4)∠ABN=30°;
(3):不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=eq \f(1,2)∠PBN=eq \f(1,2)∠APB,
即∠APB∶∠ADB=2∶1.
初中数学北师大版八年级下册第二章 一元一次不等式和一元一次不等式组综合与测试精品精练: 这是一份初中数学北师大版八年级下册第二章 一元一次不等式和一元一次不等式组综合与测试精品精练,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版七年级下册第二章 相交线与平行线综合与测试精品单元测试课堂检测: 这是一份初中数学北师大版七年级下册第二章 相交线与平行线综合与测试精品单元测试课堂检测,文件包含第二章相交线与平行线原卷版docx、第二章相交线与平行线答案版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
北师大版七年级下册第三章 变量之间的关系综合与测试优秀单元测试随堂练习题: 这是一份北师大版七年级下册第三章 变量之间的关系综合与测试优秀单元测试随堂练习题,文件包含第三章变量之间的关系单元测试卷原卷版docx、第三章变量之间的关系单元测试卷答案版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。













