2018-2019学年天津河东区九年级上期末数学模拟检测试题（含答案）

天津市河东区2018-2019学年九年级（上）期末数学模拟检

测试题

一．选择题（共12小题，满分36分）

1．方程 （x﹣5）（x﹣6）=x﹣5 的解是（　　）

A．x=5 B．x=5  或x=6 

C．x=7 D．x=5    或 x=7

2．下列抛物线中，与抛物线y=﹣3x2+1的形状、开口方向完全相同，且顶点坐标为（﹣1，2）的是（　　）

A．y=﹣3（x+1）2+2 B．y=﹣3（x﹣1）2+2 

C．y=﹣（3x﹣1）2+2 D．y=﹣（3x﹣1）2+2

3．下列图案中既是中心对称图形，又是轴对称图形的是（　　）

A． B． 

C． D．

4．抛物线y=3（x﹣2）2+5的顶点坐标是（　　）

A．（﹣2，5） B．（﹣2，﹣5） C．（2，5） D．（2，﹣5）

5．在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是，则n的值为（　　）

A．10 B．8 C．5 D．3

6．已知关于x的一元二次方程3x2+4x﹣5=0，下列说法正确的是（　　）

A．方程有两个相等的实数根 

B．方程有两个不相等的实数根 

C．没有实数根 

D．无法确定

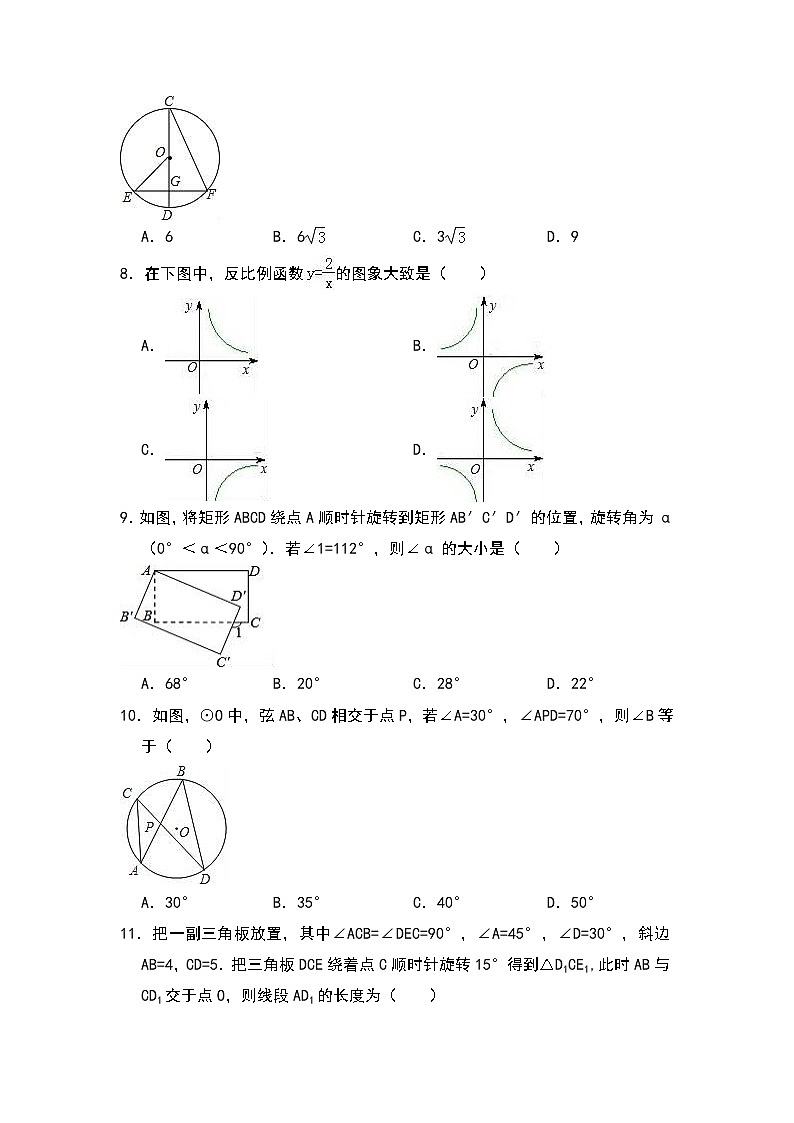
7．如图，⊙O的半径为6，直径CD过弦EF的中点G，若∠EOD=60°，则弦CF的长等于（　　）

A．6 B．6 C．3 D．9

8．在下图中，反比例函数的图象大致是（　　）

A． B． 

C． D．

9．如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°）．若∠1=112°，则∠α的大小是（　　）

A．68° B．20° C．28° D．22°

10．如图，⊙O中，弦AB、CD相交于点P，若∠A=30°，∠APD=70°，则∠B等于（　　）

A．30° B．35° C．40° D．50°

11．把一副三角板放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=4，CD=5．把三角板DCE绕着点C顺时针旋转15°得到△D1CE1,此时AB与CD1交于点O，则线段AD1的长度为（　　）

A． B． C． D．4

12．点P反比例函数y=﹣的图象上，过点P分别作坐标轴的垂线段PM、PN，则四边形OMPN的面积=（　　）

A． B．2 C．2 D．1

二．填空题（共6小题，满分18分，每小题3分）

13．点A（x1，y1）、B（x2，y2）在二次函数y=x2﹣4x﹣1的图象上，若当1＜x1＜2，3＜x2＜4时，则y1与y2的大小关系是y1　   　y2．（用“＞”、“＜”、“=”填空）

14．若函数y=的图象在其所在的每一象限内，函数值y随自变量x的增大而减小，则m的取值范围是　   　．

15．小明掷一枚均匀的骰子，骰子的六个面上分别刻有1，2，3，4，5，6点，得到的点数为奇数的概率是　   　．

16．如图，PA、PB分别与⊙O相切于A、B两点，若∠C=65°，则∠P的度数为　   　．

17．如图，正五边形ABCDE和正三角形AMN都是⊙O的内接多边形，则∠BOM=　   　．

18．已知二次函数y=ax2+bx+c（a≠0）的图象如图，有下列6个结论：

①abc＜0；

②b＜a﹣c；

③4a+2b+c＞0；

④2c＜3b；

⑤a+b＜m（am+b），（m≠1的实数）

⑥2a+b+c＞0，其中正确的结论的有　   　．

三．解答题（共7小题，满分66分）

19．（8分）用适当的方法解下列方程：

（1）x2﹣3x=0

（2）x2﹣4x+2=0

（3）x2﹣x﹣6=0

（4）（x+1）（x﹣2）=4﹣2x

20．（8分）已知A=（ab≠0且a≠b）

（1）化简A；

（2）若点P（a，b）在反比例函数y=﹣的图象上，求A的值．

21．（10分）如图，在一个可以自由转动的转盘中，指针位置固定，三个扇形的面积都相等，且分别标有数字1，2，3．

（1）小明转动转盘一次，当转盘停止转动时，指针所指扇形中的数字是奇数的概率为　   　；

（2）小明先转动转盘一次，当转盘停止转动时，记录下指针所指扇形中的数字；接着再转动转盘一次，当转盘停止转动时，再次记录下指针所指扇形中的数字，求这两个数字之和是3的倍数的概率（用画树状图或列表等方法求解）．

22．（10分）如图，已知⊙O是以AB为直径的△ABC的外接圆，过点A作⊙O的切线交OC的延长线于点D，交BC的延长线于点E．

（1）求证：∠DAC=∠DCE；

（2）若AB=2，sin∠D=，求AE的长．

23．（10分）小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．

（1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．

（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？

（3）如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本=进价×销售量）

24．（10分）如图，△ABC中，AB=AC，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D

（1）求证：BE=CF；

（2）当四边形ACDE为平行四边形时，求证：△ABE为等腰直角三角形．

25．（10分）如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．

（1）求二次函数的表达式；

（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；

（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从 点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．

参考答案

一．选择题

1．解：方程移项得：（x﹣5）（x﹣6）﹣（x﹣5）=0，

分解因式得：（x﹣5）（x﹣7）=0，

解得：x=5或x=7，

故选：D．

2．解：

∵抛物线顶点坐标为（﹣1，2），

∴可设抛物线解析式为y=a（x+1）2+2，

∵与抛物线y=﹣3x2+1的形状、开口方向完全相同，

∴a=﹣3，

∴所求抛物线解析式为y=﹣3（x+1）2+2，

故选：A．

3．解：A、是轴对称图形，不是中心对称图形，故错误；

B、是轴对称图形，不是中心对称图形，故错误；

C、是轴对称图形，又是中心对称图形，故正确；

D、是轴对称图形，不是中心对称图形，故错误．

故选：C．

4．解：抛物线y=3（x﹣2）2+5的顶点坐标为（2，5），

故选：C．

5．解：∵在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是，

∴=，

解得n=8．

故选：B．

6．解：∵△=42﹣4×3×（﹣5）=76＞0，

∴方程有两个不相等的实数根．

故选：B．

7．解：连接DF，

∵直径CD过弦EF的中点G，

∴=，

∴∠DCF=∠EOD=30°，

∵CD是⊙O的直径，

∴∠CFD=90°，

∴CF=CD•cos∠DCF=12×=6，

故选：B．

8．解：∵k=2，可根据k＞0，反比例函数图象在第一、三象限；

∴在每个象限内，y随x的增大而减小．

故选：D．

9．解：∵四边形ABCD为矩形，

∴∠BAD=∠ABC=∠ADC=90°，

∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α，

∴∠BAB′=α，∠B′AD′=∠BAD=90°，∠AD′C′=∠ADC=90°，

∵∠2=∠1=112°，

而∠ABC=∠D′=90°，

∴∠3=180°﹣∠2=68°，

∴∠BAB′=90°﹣68°=22°，

即∠α=22°．

故选：D．

10．解：∵∠APD是△APC的外角，

∴∠APD=∠C+∠A；

∵∠A=30°，∠APD=70°，

∴∠C=∠APD﹣∠A=40°；

∴∠B=∠C=40°；

故选：C．

11．解：由题意易知：∠CAB=45°，∠ACD=30°．

若旋转角度为15°，则∠ACO=30°+15°=45°．

∴∠AOC=180°﹣∠ACO﹣∠CAO=90°．

在等腰Rt△ABC中，AB=4，则AC=BC=2．

同理可求得：AO=OC=2．

在Rt△AOD1中，OA=2，OD1=CD1﹣OC=3，

由勾股定理得：AD1=．

故选：A．

12．解：∵点P反比例函数y=﹣的图象上，

∴过点P分别作坐标轴的垂线段PM、PN，所得四边形OMPN的面积为|﹣2|=2．

故选：C．

二．填空题（共6小题，满分18分，每小题3分）

13．解：由二次函数y=x2﹣4x﹣1=（x﹣2）2﹣5可知，其图象开口向上，且对称轴为x=2，

∵1＜x1＜2，3＜x2＜4，

∴A点横坐标离对称轴的距离小于B点横坐标离对称轴的距离，

∴y1＜y2．

故答案为：＜．

14．解：∵函数y=的图象在每一象限内y的值随x值的增大而减小，

∴m﹣2＞0，

解得m＞2．

故答案为：m＞2．

15．解：根据题意知，掷一次骰子6个可能结果，而奇数有3个，所以掷到上面为奇数的概率为．

故答案为：．

16．解：∵PA、PB是⊙O切线，

∴PA⊥OA，PB⊥OB，

∴∠PAO=∠PBO=90°，

∵∠P+∠PAO+∠AOB+∠PBO=360°，

∴∠P=180°﹣∠AOB，

∵∠ACB=65°，

∴∠AOB=2∠ACB=130°，

∴∠P=180°﹣130°=50°，

故答案为50°．

17．解：连接OA，

∵五边形ABCDE是正五边形，

∴∠AOB==72°，

∵△AMN是正三角形，

∴∠AOM==120°，

∴∠BOM=∠AOM﹣∠AOB=48°，

故答案为：48°．

18．解：①∵该抛物线开口方向向下，

∴a＜0．

∵抛物线对称轴在y轴右侧，

∴a、b异号，

∴b＞0；

∵抛物线与y轴交于正半轴，

∴c＞0，

∴abc＜0；

故①正确；

②∵a＜0，c＞0，

∴a﹣c＜0，

∵b＞0，

∴b＞a﹣c，

故②错误；

③根据抛物线的对称性知，当x=2时，y＞0，即4a+2b+c＞0；故③正确；

④∵对称轴方程x=﹣=1，

∴b=﹣2a，

∴a=﹣b，

∵当x=﹣1时，y=a﹣b+c＜0，

∴﹣b+c＜0，

∴2c＜3b，

故④正确；

⑤∵x=m对应的函数值为y=am2+bm+c，

x=1对应的函数值为y=a+b+c，

又x=1时函数取得最大值，

当m≠1时，a+b+c＞am2+bm+c，即a+b＞am2+bm=m（am+b），

故⑤错误．

⑥∵b=﹣2a，

∴2a+b=0，

∵c＞0，

∴2a+b+c＞0，

故⑥正确．

综上所述，其中正确的结论的有：①③④⑥．

故答案为：①③④⑥．

三．解答题（共7小题，满分66分）

19．解：（1）x2﹣3x=0，

x（x﹣3）=0，

x=0，x﹣3=0，

x1=0，x2=3；

（2）移项，得

x2﹣4x=﹣2，

配方，得

x2﹣4x+4=2，

即（x﹣2）2=2，

开方，得

x﹣2=，

x1=2+，x2=2﹣；

（3）x2﹣x﹣6=0

（x﹣3）（x+2）=0，

x﹣3=0，x+2=0，

x1=3，x2=﹣2；

（4）（x+1）（x﹣2）=4﹣2x

（x+1）（x﹣2）﹣2（x﹣2）=0

（x﹣2）（x+1﹣2）=0，

x﹣2=0或x﹣1=0，

x1=2，x2=1．

20．解：（1）A=，

=，

=，

=．

（2）∵点P（a，b）在反比例函数y=﹣的图象上，

∴ab=﹣5，

∴A==﹣．

21．解：（1）∵在标有数字1、2、3的3个转盘中，奇数的有1、3这2个，

∴指针所指扇形中的数字是奇数的概率为，

故答案为：；

（2）列表如下：

由表可知，所有等可能的情况数为9种，其中这两个数字之和是3的倍数的有3种，

所以这两个数字之和是3的倍数的概率为=．

22．解：（1）∵AD是圆O的切线，

∴∠DAB=90°．

∵AB是圆O的直径，

∴∠ACB=90°．

∵∠DAC+∠CAB=90°，∠CAB+∠ABC=90°，

∴∠DAC=∠B．

∵OC=OB，

∴∠B=∠OCB．

又∵∠DCE=∠OCB．

∴∠DAC=∠DCE．

（2）∵AB=2，

∴AO=1．

∵sin∠D=，

∴OD=3，DC=2．

在Rt△DAO中，由勾股定理得AD==2．

∵∠DAC=∠DCE，∠D=∠D，

∴△DEC∽△DCA．

∴，即．

解得：DE=．

∴AE=AD﹣DE=．

23．解：（1）由题意，得：w=（x﹣20）•y=（x﹣20）•（﹣10x+500）=﹣10x2+700x﹣10000，即w=﹣10x2+700x﹣10000（20≤x≤32）

（2）对于函数w=﹣10x2+700x﹣10000的图象的对称轴是直线．

又∵a=﹣10＜0，抛物线开口向下．∴当20≤x≤32时，W随着X的增大而增大，

∴当x=32时，W=2160

答：当销售单价定为32元时，每月可获得最大利润，最大利润是2160元．

（3）取W=2000得，﹣10x2+700x﹣10000=2000

解这个方程得：x1=30，x2=40．

∵a=﹣10＜0，抛物线开口向下．

∴当30≤x≤40时，w≥2000．

∵20≤x≤32

∴当30≤x≤32时，w≥2000．

设每月的成本为P（元），由题意，得：P=20（﹣10x+500）=﹣200x+10000

∵k=﹣200＜0，

∴P随x的增大而减小．

∴当x=32时，P的值最小，P最小值=3600．

答：想要每月获得的利润不低于2000元，小明每月的成本最少为3600元．

24．解：（1）证明：∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，

∴AE=AB，AF=AC，∠EAF=∠BAC，

∴∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，

∵AB=AC，

∴AE=AF，

∴△AEB可由△AFC绕点A按顺时针方向旋转得到，

∴BE=CF；

（2）在□ABCD中，∠EAC+∠ACF=180°

∴∠EAF=∠BAC=45°

∴∠FAB+∠ACF=90°

又AF=AC

∴∠F=∠ACF

∴∠FAB+∠F=90°

∴∠ACF=45°

∴△AFC为等腰直角三角形

∴△ABE为等腰直角三角形

25．解：（1）把A（1，0）和C（0，3）代入y=x2+bx+c，

解得：b=﹣4，c=3，

∴二次函数的表达式为：y=x2﹣4x+3；

（2）令y=0，则x2﹣4x+3=0，

解得： x=1或x=3，

∴B（3，0），

∴BC=3，

点P在y轴上，当△PBC为等腰三角形时分三种情况进行讨论：如图1，

①当CP=CB时，PC=3，∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3

∴P1（0，3+3），P2（0，3﹣3）；

②当BP=BC时，OP=OB=3，

∴P3（0，﹣3）；

③当PB=PC时，

∵OC=OB=3

∴此时P与O重合，

∴P4（0，0）；

综上所述，点P的坐标为：（0，3+3）或（0，3﹣3）或（0，﹣3）或（0，0）；

（3）如图2，设A运动时间为t，由AB=2，得BM=2﹣t，则DN=2t，

∴S△MNB=×（2﹣t）×2t=﹣t2+2t=﹣（t﹣1）2+1，

即当M（2，0）、N（2，2）或（2，﹣2）时△MNB面积最大，最大面积是1．