2018-2019学年福建省龙岩市上杭县九年级上期中考试数学试题（含答案）

龙岩市上杭县2018-2019学年上学期期中考试九年级数学试题

（考试时间：120分钟   满分150分）

一、选择题（每小题4分，共40分）

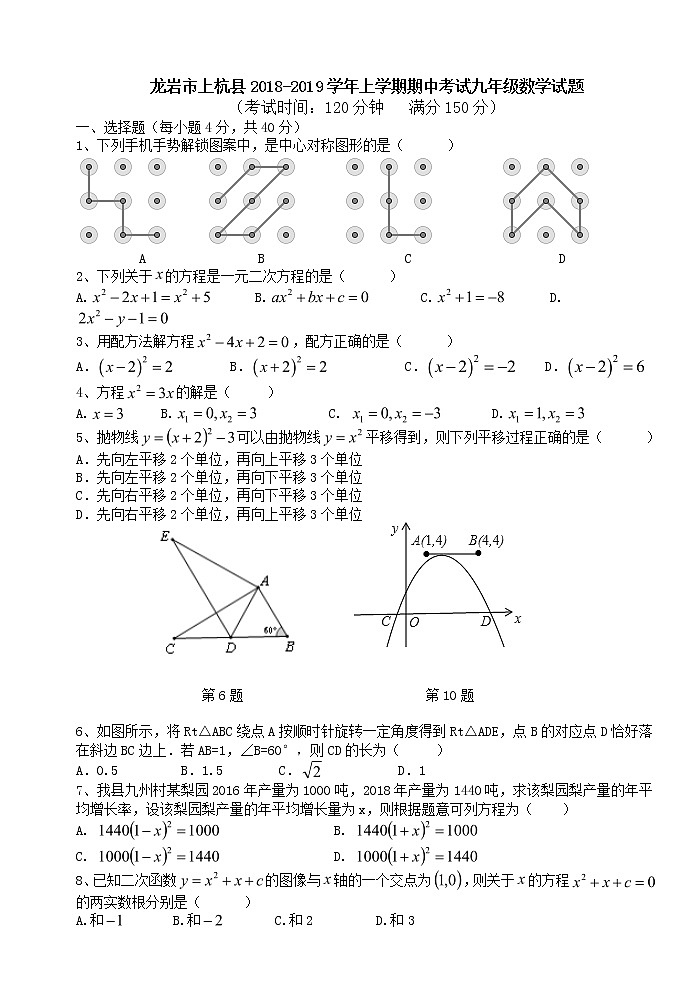
1、下列手机手势解锁图案中，是中心对称图形的是（      ）

         A                B                    C                     D

2、下列关于的方程是一元二次方程的是（      ）

A.      B.       C.      D.

3、用配方法解方程，配方正确的是（      ）

A．       B．     C．    D．

4、方程的解是（     ）

A.     B.          C.        D.

5、抛物线可以由抛物线平移得到，则下列平移过程正确的是（　  　）

A．先向左平移2个单位，再向上平移3个单位 

B．先向左平移2个单位，再向下平移3个单位

C．先向右平移2个单位，再向下平移3个单位 

D．先向右平移2个单位，再向上平移3个单位

第6题                          第10题

6、如图所示，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在斜边BC边上．若AB=1，∠B=60°，则CD的长为（     ）

A．0.5     B．1.5   C．     D．1

7、我县九州村某梨园2016年产量为1000吨，2018年产量为1440吨，求该梨园梨产量的年平均增长率，设该梨园梨产量的年平均增长量为x，则根据题意可列方程为（　　）

A.                 B.

C.                 D.

8、已知二次函数的图像与轴的一个交点为，则关于的方程的两实数根分别是（      ）

A.和       B.和       C.和2         D.和3

9、若函数的图象与坐标轴有三个交点，则b的取值范围是（　  　）
A.b＜1且b≠0 B.b＞1      C.0＜b＜1    D.b＜1

10、如图，点 A，B 的坐标分别为（1，4）和（4，4）， 抛物线 的顶点在线段 AB 上运动（抛物线随顶点一起平移），与 x 轴交于 C、 D 两点（C 在 D 的左侧），点C 的横坐标最小值为，则点 D 的横坐标最大值为（      ）

A．﹣3          B．1               C．5              D．8

二、填空题（每小题4分，共24分）

11、若是二次函数，则=       。

12、菱形的两条对角线分别是方程的两实根，则菱形的面积为          。

13、已知是关于的方程的一个根，则        。

14、已知抛物线经过点，，则_____（填“＞”，“=”，或“＜”）．

15、如图，在平面直角坐标系中，点A在抛物线上运动，过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连接BD，则对角线BD的最小值为　   　。

第15题                                    第16题

16、如图，二次函数的图象与轴交于两点，与轴交于点，且，则下列结论：

其中正确的结论是       。（只填写序号）

三、解答题（9小题，共86分）

17、（8分）解方程

（1）                   

（2）

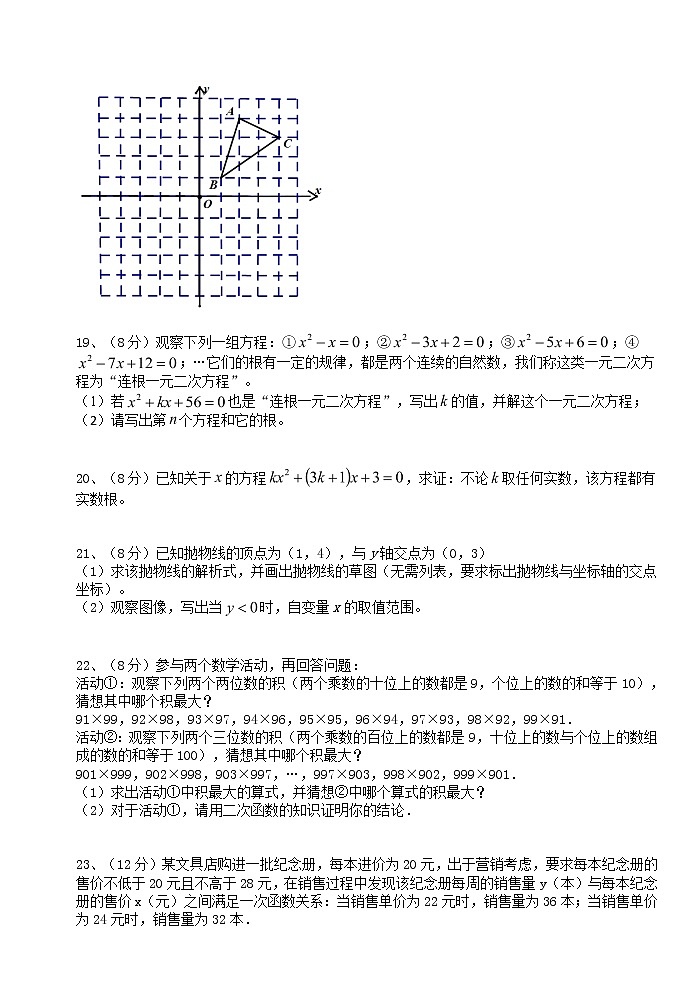
18、（8分）如图，三个顶点的坐标分别为，，.

（1）请画出关于原点对称的，并写出的坐标；

（2）请画出绕点逆时针旋转后的。

19、（8分）观察下列一组方程：①；②；③；④；…它们的根有一定的规律，都是两个连续的自然数，我们称这类一元二次方程为“连根一元二次方程”。

（1）若也是“连根一元二次方程”，写出的值，并解这个一元二次方程；

（2）请写出第个方程和它的根。

20、（8分）已知关于的方程，求证：不论取任何实数，该方程都有实数根。

21、（8分）已知抛物线的顶点为（1，4），与y轴交点为（0，3）

（1）求该抛物线的解析式，并画出抛物线的草图（无需列表，要求标出抛物线与坐标轴的交点坐标）。

（2）观察图像，写出当时，自变量x的取值范围。

22、（8分）参与两个数学活动，再回答问题：
活动①：观察下列两个两位数的积（两个乘数的十位上的数都是9，个位上的数的和等于10），猜想其中哪个积最大？
91×99，92×98，93×97，94×96，95×95，96×94，97×93，98×92，99×91．
活动②：观察下列两个三位数的积（两个乘数的百位上的数都是9，十位上的数与个位上的数组成的数的和等于100），猜想其中哪个积最大？
901×999，902×998，903×997，…，997×903，998×902，999×901．
（1）求出活动①中积最大的算式，并猜想②中哪个算式的积最大？
（2）对于活动①，请用二次函数的知识证明你的结论．

23、（12分）某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

（1）请直接写出y与x的函数关系式；

（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

（3）设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

24、（12分）（1）如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，求∠EAF的度数．

（2）如图②，在Rt△ABD中，∠BAD=90°，AB=AD，点M，N是BD边上的任意两点，且∠MAN=45°，将△ABM绕点A逆时针旋转90°至△ADH位置，连接NH，试判断MN，ND，DH之间的数量关系，并说明理由．

（3）在图①中，连接BD分别交AE，AF于点M，N，若EG=4，GF=6，BM=，求AG，MN的长．

25、（14分）已知，抛物线与直线有一个公共点M（1，0），且a＜b．

（1）求与的关系式和抛物线的顶点D坐标（用的代数式表示）；

（2）直线与抛物线的另外一个交点记为N，求△DMN的面积（用的代数式表示）；

（3）时，直线与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移个单位，若线段GH与抛物线有两个不同的公共点，请直接写出t的取值范围．

参考答案

一、选择题（本大题共10小题，每小题4分，共40分）

二、填空题（本大题共6小题，每小题3分，共18分）

11．；     12．24；     13．6;      14．>   15、8    16、①③④   

三、解答题

17．解： （1）因式分解得   ……………2 分 

……………3 分

……………4 分

（2） ……………1 分

             ……………2 分

……………3 分

……………4 分

18、（1）( -2   ,  -4  )  (  -1  ,  -1  )   ( -4   , -3   ) ………3 分

         画出……………5 分

    （2）画出……………8 分

19、（1）   ……………2 分 

         解方程得 ……………4 分 

    （2）   ……………6 分   

           ……………8 分 

20、证明：当时，方程为 解得 方程有实数根……………2 分 

         当时，方程有两个实数根…………7 分 

  综上所述，方程总有实数根   ...........................8分

21、解：（1）依题意可设：，……………1 分

把（0,3）代入上式得，解得：……………2 分

　　  ∴二次函数的解析式为：． ……………3 分

画草图……………5分

（2）……………8 分

22、解：①∵91×99=9009，92×98=9016，93×97=9021，94×96=9024，95×95=9025，…
∴95×95的积最大；…………2 分
②由①中规律可得950×950的积最大；……………3 分

（2）证明：将①中的算式设为（90+x）（90-x）（x=1，2，3，4，5，6，7，8，9），
（90+x）（90-x）……………5 分

……………6 分

∵a<0，
∴当x=5时，它有最大值9025，
即95×95的积最大．..............................8分

23、解：y＝－2x＋80(20≤x≤28)．……………3 分

(2)   设当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是x元，根据题意，得(x－20)y＝150，则(x－20)(－2x＋80)＝150，

整理，得x2－60x＋875＝0，(x－25)(x－35)＝0，……………5 分

解得x1＝25，x2＝35(不合题意舍去)，……………6 分

答：每本纪念册的销售单价是25元．……………7 分

(3)    由题意可得w＝(x－20)(－2x＋80)

＝－2x2＋120x－1600

＝－2(x－30)2＋200，……………10 分

此时当x＝30时，w最大，又∵售价不低于20元且不高于28元，x＜30时，y随x的增大而增大，∴当x＝28时，w最大＝－2(28－30)2＋200＝192(元)，…………11 分

答：该纪念册销售单价定为28元时，才能使文具店销售该纪念册所获利润最大，最大利润是192元． ……………12 分

24、（1）在Rt△ABE和Rt△AGE中，AB=AG，AE=AE，
∴Rt△ABE≌Rt△AGE（HL）．
∴∠BAE=∠GAE．……………1 分
同理，∠GAF=∠DAF．
∴．……………3分

（1）MN2=ND2+DH2．……………4 分
∵∠BAM=∠DAH，∠BAM+∠DAN=45°，
∴∠HAN=∠DAH+∠DAN=45°．
∴∠HAN=∠MAN．
又∵AM=AH，AN=AN，
∴△AMN≌△AHN．
∴MN=HN．     ……………6 分

∵∠BAD=90°，AB=AD，
∴∠ABD=∠ADB=45°．
∴∠HDN=∠HDA+∠ADB=90°．
∴NH2=ND2+DH2．
∴MN2=ND2+DH2．……………7 分
（3）由（1）知，BE=EG，DF=FG．
设AG=x，则CE=x-4，CF=x-6．
在Rt△CEF中，
∵，
∴．
解这个方程，得（舍去）．
即AG=12．      ……………9 分
在Rt△ABD中，
∴．
由（2）可知，……………10 分
设MN=a，则，
解得即．……………12 分

25、解：（1）∵抛物线有一个公共点M（1，0），

∴，即，……………2 分

∴

，

∴抛物线顶点D的坐标为；……………4分

（2）∵直线经过点M（1，0），

∴0=2×1+m，解得m=﹣2，……………5分

∴y=2x﹣2，

由，

得，

解得x=1或，

∴N点坐标为，……………7分

∵a＜b，即a＜﹣2a，   ∴a＜0，

设抛物线对称轴交直线于点E，

∵抛物线对称轴为，∴E（﹣，﹣3），……………8分

∵M（1，0），N，

设△DMN的面积为S，

∴……………10分

(3)、t的取值范围是2≤t＜．……………14分