





2021版《5年中考3年模拟》全国版中考数学:§3.4 二次函数
展开考点一 二次函数的图象与性质
1.(2018山西,9,3分)用配方法将二次函数y=x2-8x-9化为y=a(x-h)2+k的形式为( )A.y=(x-4)2+7 B.y=(x-4)2-25C.y=(x+4)2+7 D.y=(x+4)2-25
答案 B y=x2-8x-9=x2-8x+16-16-9=(x-4)2-25,故选B.
2.(2019甘肃兰州,11,4分)已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是 ( )A.2>y1>y2 B.2>y2>y1C.y1>y2>2 D.y2>y1>2
答案 A 由y=-(x+1)2+2知,抛物线开口向下,对称轴为直线x=-1,y的最大值为2,在对称轴右侧,y随x的增 大而减小,又∵1<2,∴2>y1>y2,故选A.
3.(2020四川成都,10,3分)关于二次函数y=x2+2x-8,下列说法正确的是 ( )A.图象的对称轴在y轴的右侧B.图象与y轴的交点坐标为(0,8)C.图象与x轴的交点坐标为(-2,0)和(4,0)D.y的最小值为-9
4.(2020陕西,10,3分)在平面直角坐标系中,将抛物线y=x2-(m-1)x+m(m>1)沿y轴向下平移3个单位,则平移 后得到的抛物线的顶点一定在 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限
5.(2019陕西,10,3分)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对 称,则符合条件的m、n的值分别为( )A. ,- B.5,-6 C.-1,6 D.1,-2
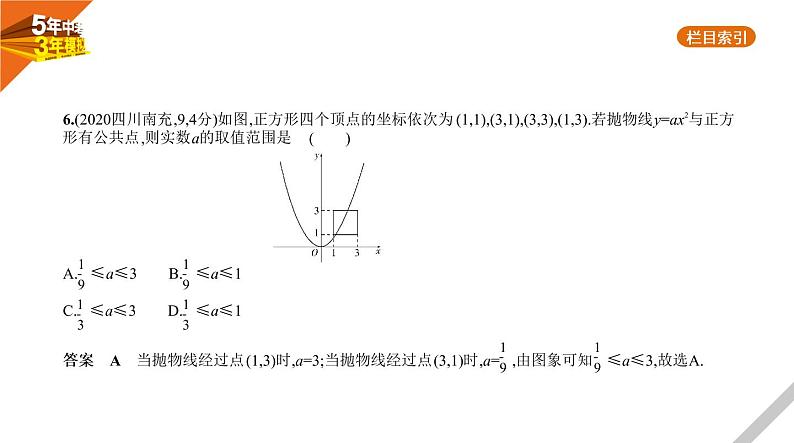
6.(2020四川南充,9,4分)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方 形有公共点,则实数a的取值范围是 ( ) A. ≤a≤3 B. ≤a≤1C. ≤a≤3 D. ≤a≤1
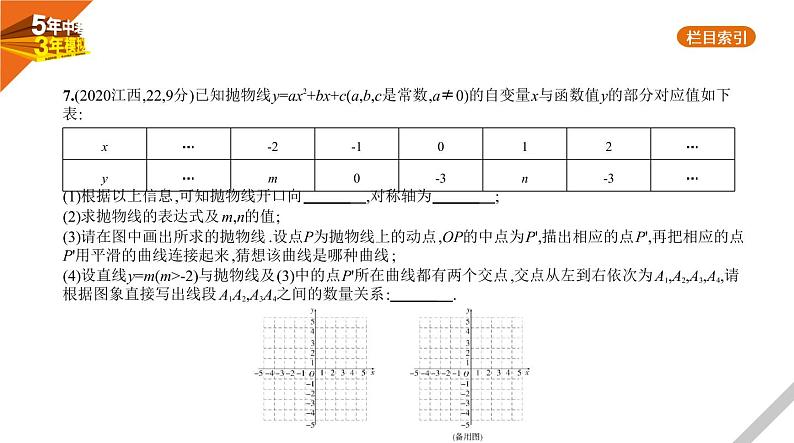
7.(2020江西,22,9分)已知抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下 表:
(1)根据以上信息,可知抛物线开口向 ,对称轴为 ;(2)求抛物线的表达式及m,n的值;(3)请在图中画出所求的抛物线.设点P为抛物线上的动点,OP的中点为P',描出相应的点P',再把相应的点 P'用平滑的曲线连接起来,猜想该曲线是哪种曲线;(4)设直线y=m(m>-2)与抛物线及(3)中的点P'所在曲线都有两个交点,交点从左到右依次为A1,A2,A3,A4,请 根据图象直接写出线段A1A2,A3A4之间的数量关系: .
解析 (1)上;直线x=1.详解:由x=-1,y=0;x=0,y=-3;x=2,y=-3,可知抛物线开口向上.由题表可知:x=0,y=-3;x=2,y=-3,根据二次函数图象的对称性可知抛物线的对称轴为直线x= =1.(2)由题表可知抛物线过点(0,-3).∴y=ax2+bx-3.将(-1,0),(2,-3)代入,得 解得 ∴y=x2-2x-3.当x=-2时,m=(-2)2-2×(-2)-3=5;当x=1时,n=12-2×1-3=-4.(3)如图1所示,点P'所在曲线是抛物线.详解:设P(x',y'),P'(x,y),∵P'是OP的中点,∴x'=2x,y'=2y,代入点P所在图象的表达式可得2y=(2x)2-2×2x-3,即
y=2x2-2x- ,为点P'所在曲线的表达式,∴点P'所在曲线是抛物线.(4)A3A4-A1A2=1.详解:如图2.设点A1,A2,A3,A4对应的横坐标分别为x1,x2,x3,x4,∴A1A2=x2-x1,A3A4=x4-x3,∴A3A4-A1A2=x4-x3-(x2-x1) =x4+x1-(x3+x2),令y=x2-2x-3=m,可得x2-2x-3-m=0,它对应的两个根应为x1,x4,∴x1+x4=2,令y=2x2-2x- =m,可得2x2-2x- -m=0,它对应的两个根应为x2,x3,∴x2+x3=1,∴A3A4-A1A2=2-1=1.
8.(2019云南,21,8分)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.(1)求k的值;(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
易错警示 (1)抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=- .(2)点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|,二者容易混淆,从而导致失分.
考点二 系数a、b、c的作用
1.(2020云南昆明,13,4分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,-2),点A(-1, m)在抛物线上,则下列结论中错误的是 ( ) A.ab<0B.一元二次方程ax2+bx+c=0的正实数根在2和3之间C.a= D.点P1(t,y1),P2(t+1,y2)在抛物线上,当实数t> 时,y1
答案 D 由抛物线开口向上可得a>0.∵抛物线的对称轴x=- 在y轴右侧,∴- >0,而a>0,∴b<0.由抛物线与y轴的交点在y轴正半轴上可得c>0.当a>0,b<0时,一次函数y=ax+b的图象经过第一、三、四象限;当c>0时,反比例函数y= 的图象经过第一、三象限,故选D.
3.(2019天津,12,3分)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
且当x=- 时,与其对应的函数值y>0.有下列结论:①abc>0;②-2和3是关于x的方程ax2+bx+c=t的两个根;③0
考点三 二次函数与方程、不等式之间的关系
解题关键 明确该抛物线的对称轴为y轴是解题关键.
2.(2020贵州贵阳,10,3分)已知二次函数y=ax2+bx+c的图象经过(-3,0)与(1,0)两点,关于x的方程ax2+bx+c+m =0(m>0)有两个根,其中一个根是3,则关于x的方程ax2+bx+c+n=0(0
答案 C 令ax2-x+1= x+ ,即ax2- x+ =0,若直线与抛物线有两个不同的交点,则有 -4× a>0,解得a< .若抛物线与线段AB有两个不同的交点,则①当a<0时, 解得a≤-2,∴a≤-2;②当a>0时, 解得a≥1,∴1≤a< .综上所述,1≤a< 或a≤-2,故选C.
4.(2019辽宁大连,10,3分)如图,抛物线y=- x2+ x+2与x轴相交于A,B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与抛物线交于P,Q两点,则线段PQ的长为 ( ) A.3 B.1+ C.4 D.2
答案 D 在y=- x2+ x+2中,令x=0,则y=2,∴C(0,2);令y=0,则- x2+ x+2=0,解得x=-2或4,∴A(-2,0).∵CD∥AB,∴点D的纵坐标和点C的纵坐标相同,为2,令y=2,则- x2+ x+2=2,解得x=0或2,∴D(2,2).设直线AD的解析式为y=kx+b(k≠0),将(-2,0),(2,2)代入y=kx+b中,得 解得 ∴直线AD的解析式为y= x+1,令y= x+1中的x=0,则y=1,∴E(0,1).令- x2+ x+2=1,即x2-2x-4=0,解得x=1± ,所以PQ=(1+ )-(1- )=2 ,故选D.
思路分析 根据抛物线的解析式求出抛物线与x轴的交点A,与y轴的交点C的坐标,因为CD∥AB,所以点 D的纵坐标和点C的纵坐标相同,将点D的纵坐标代入抛物线解析式中,从而求出点D的坐标.利用待定系 数法求直线AD的解析式,并进一步求出点E的坐标,将点E的纵坐标代入抛物线的解析式中,求出点P、Q 的横坐标,进而可求出PQ的长.
5.(2018天津,12,3分)已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(-1,0),(0,3),其对称轴在y轴右侧.有 下列结论:①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;③-3
解析 ∵抛物线过点A(-1,m),B(5,m),∴(-1)2-b+1=52+5b+1,解得b=-4,∴y=x2-4x+1=(x-2)2-3,∴抛物线的顶 点坐标为(2,-3).将抛物线y=(x-2)2-3向上平移n(n是正整数)个单位,使平移后的图象与x轴没有交点,则n>3. ∴n的最小值为4.
7.(2020宁夏,10,3分)若二次函数y=-x2+2x+k的图象与x轴有两个交点,则k的取值范围是 .
解析 若二次函数y=-x2+2x+k的图象与x轴有两个交点,则Δ=4+4k>0,解得k>-1.
8.(2019湖北武汉,15,3分)抛物线y=ax2+bx+c经过A(-3,0),B(4,0)两点,则关于x的一元二次方程a(x-1)2+c=b- bx的解是 .
答案 x1=-2,x2=5
1.(2019浙江温州,9,4分)已知二次函数y=x2-4x+2,关于该函数在-1≤x≤3的取值范围内,下列说法正确的 是( )A.有最大值-1,有最小值-2B.有最大值0,有最小值-1C.有最大值7,有最小值-1D.有最大值7,有最小值-2
2.(2018陕西,10,3分)对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限
3.(2018湖北黄冈,6,3分)当a≤x≤a+1时,函数y=x2-2x+1的最小值为1,则a的值为 ( )A.-1 B.2 C.0或2 D.-1或2
答案 D y=x2-2x+1=(x-1)2,当a≥1时,在a≤x≤a+1时,y随x的增大而增大,函数的最小值为a2-2a+1,则a2-2 a+1=1,解得a=2或a=0(舍去);当a+1≤1,即a≤0时,在a≤x≤a+1时,y随x的增大而减小,函数的最小值为(a+ 1)2-2(a+1)+1=a2,则a2=1,解得a=-1或a=1(舍去);当0
答案 A 直接根据二次函数图象“左加右减,上加下减”的平移规律进行解答即可.选A.
5.(2020四川南充,10,4分)关于二次函数y=ax2-4ax-5(a≠0)的三个结论:①对任意实数m,都有x1=2+m与x2=2 -m对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则-
思路分析 由题意可得抛物线的对称轴为直线x=- =2,由对称性可判断①正确;分a>0和a<0两种抛物线开口方向讨论②③,当x=3时,y=-3a-5,当x=4时,y=-5.根据函数图象的性质可得-3a-5≤y≤-5或-5≤y≤-3 a-5.当3≤x≤4时,对应的y的整数值有4个,可以得出-3a-5的取值范围,进而得出a的取值范围,判断出②正 确;抛物线与x轴交于不同两点,说明Δ=16a2+20a>0.然后根据AB≤6,可得当x=5时函数值y满足的条件,得 出a的取值范围,进而可知③正确.
6.(2020内蒙古呼和浩特,7,3分)关于二次函数y= x2-6x+a+27,下列说法错误的是 ( )A.若将图象向上平移10个单位,再向左平移2个单位后过点(4,5),则a=-5B.当x=12时,y有最小值a-9C.x=2对应的函数值比最小值大7D.当a<0时,图象与x轴有两个不同的交点
答案 C y= x2-6x+a+27= (x-12)2+a-9,将图象向上平移10个单位,再向左平移2个单位后,所得图象对应的二次函数解析式为y= (x-10)2+a+1,当x=4,y=5时,5= ×(4-10)2+a+1,解得a=-5,故A中说法正确.当x=12时,ymin=a-9,故B中说法正确.当x=2时,y= ×(2-12)2+a-9=a+16,a+16-(a-9)=25,故C中说法错误.∵Δ=(-6)2-4× ×(a+27)=36-a-27=9-a,∴当a<0时,Δ>0,图象与x轴有两个不同的交点,故D中说法正确.故选C.
7.(2020江西,6,3分)在平面直角坐标系中,点O为坐标原点,抛物线y=x2-2x-3与y轴交于点A,与x轴正半轴交 于点B,连接AB,将Rt△OAB向右上方平移,得到Rt△O'A'B',且点O',A'落在抛物线的对称轴上,点B'落在抛 物线上,则直线A'B'的表达式为 ( )A.y=x B.y=x+1C.y=x+ D.y=x+2
答案 B 令x=0,则y=-3,故A(0,-3).令y=0,则x2-2x-3=0,解得x1=-1,x2=3,故B(3,0),易得直线AB的表达式为y= x-3.∵将Rt△OAB向右上方平移得到Rt△O'A'B',且点O'、A'落在抛物线的对称轴x=1上,∴点B'的横坐标 为4,代入抛物线表达式可得B'(4,5).∵A'B'∥AB,∴可设直线A'B'的表达式为y=x+b,将点B'(4,5)代入可得b= 1,∴直线A'B'的表达式为y=x+1,故选B.
思路分析 首先求出点A、B的坐标,然后由待定系数法求出直线AB的表达式.因为点O、B在x轴上,所以 向右上方平移后O'B'∥x轴,A'B'∥AB,又点O'、A'落在抛物线的对称轴x=1上,可推出点B'的横坐标为4,从 而可求点B'的坐标,将点B'的坐标代入所设的直线A'B'的表达式中即可得解.
8.(2019安徽,14,5分)在平面直角坐标系中,垂直于x轴的直线l分别与函数y=x-a+1和y=x2-2ax的图象相交 于P,Q两点.若平移直线l,可以使P,Q都在x轴的下方,则实数a的取值范围是 .
答案 a>1或a<-1
解析 解法一:函数y=x2-2ax的图象与x轴的交点为(0,0),(2a,0),函数y=x-a+1的图象与x轴的交点为(a-1,0), 与y轴的交点为(0,1-a).分两种情况:①当a<0时,如图(1),要满足题意,则需a-1>2a,可得a<-1;②当a>0时,如图(2),要满足题意,则需a-1>0,可得a>1.综上,实数a的取值范围是a>1或a<-1.
难点突破 根据二次函数图象的特点分a<0和a>0两种情况考虑是解答本题的突破口.
9.(2019浙江温州,21,10分)如图,在平面直角坐标系中,二次函数y=- x2+2x+6的图象交x轴于点A,B(点A在点B的左侧).(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1 向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
解析 (1)令y=0,则- x2+2x+6=0,∴x1=-2,x2=6,∴A(-2,0),B(6,0).由函数图象得,当y≥0时,-2≤x≤6.(2)由题意得B1(6,m),∴B2(6-n,m),B3(-n,m),函数图象的对称轴为直线x= =2.∵点B2,B3在二次函数图象上且纵坐标相同,∴ =2,∴n=1,∴m=- ×(-1)2+2×(-1)+6= ,∴m,n的值分别为 ,1.
1.(2020天津,12,3分)已知抛物线y=ax2+bx+c(a,b,c是常数,a≠0,c>1)经过点(2,0),其对称轴是直线x= .有下列结论:①abc>0;②关于x的方程ax2+bx+c=a有两个不等的实数根;③a<- .其中,正确结论的个数是 ( )A.0 B.1 C.2 D.3
答案 C 抛物线的对称轴是直线x= ,即- = ,∴- =1,∴a+b=0,ab<0.①∵ab<0,c>1,∴abc<0,①错误;②抛物线经过点(2,0),将(2,0)代入得4a+2b+c=0,又∵a+b=0,∴2a+c=0,即c=-2a,方程ax2+bx+c=a可化为ax2 +bx+c-a=0,Δ=b2-4a(c-a)=b2-4ac+4a2=a2+8a2+4a2=13a2,∵a≠0,∴Δ=13a2>0,∴方程有两个不等的实数根,②正确;③∵c>1,∴c=-2a>1,∴a<- ,③正确.故正确结论的个数是2.故选C.
解题关键 本题结合一元二次方程、一元一次不等式考查二次函数的图象和性质,题目比较综合.根据 对称轴方程找到a,b的关系和将(2,0)代入得到a,c之间的关系是解题的关键.
2.(2020广东,10,3分)如图,抛物线y=ax2+bx+c的对称轴是x=1.下列结论:①abc>0;②b2-4ac>0;③8a+c<0;④5 a+b+2c>0,正确的有 ( ) A.4个 B.3个 C.2个 D.1个
3.(2020山东青岛,8,3分)已知在同一直角坐标系中,二次函数y=ax2+bx和反比例函数y= 的图象如图所示,则一次函数y= x-b的图象可能是 ( )
答案 B 由二次函数的图象可知a<0,b>0,由反比例函数的图象可知c>0,∴ <0,-b<0,∴一次函数y= x-b的图象与y轴负半轴相交且y随x的增大而减小.故选B.
4.(2019四川成都,10,3分)如图,二次函数y=ax2+bx+c的图象经过点A(1,0),B(5,0),下列说法正确的是 ( )A.c<0B.b2-4ac<0C.a-b+c<0D.图象的对称轴是直线x=3
5.(2017四川成都,10,3分)在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确 的是 ( )A.abc<0,b2-4ac>0B.abc>0,b2-4ac>0C.abc<0,b2-4ac<0D.abc>0,b2-4ac<0
思路分析 本题考查二次函数的图象与系数的关系,从抛物线的开口方向,对称轴,以及与y轴的交点位 置来判断a,b,c的符号,由抛物线与x轴的交点个数判断b2-4ac的符号.
6.(2018北京,26,6分)在平面直角坐标系xOy中,直线y=4x+4与x轴、y轴分别交于点A,B,抛物线y=ax2+bx-3a 经过点A,将点B向右平移5个单位长度,得到点C.(1)求点C的坐标;(2)求抛物线的对称轴;(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
图1将x=5代入抛物线的解析式得y=12a,∴12a≥4,∴a≥ .②a<0,且抛物线顶点不在线段BC上时,如图2.
图2将x=0代入抛物线解析式得y=-3a,∵抛物线与线段BC恰有一个公共点,∴-3a>4,∴a<- .若抛物线的顶点在线段BC上,则顶点为(1,4),如图3.
图3将(1,4)代入抛物线的解析式得4=a-2a-3a,∴a=-1.综上所述,a≥ 或a<- 或a=-1.
1.(2020广东广州,9,3分)直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是 ( )A.0个 B.1个C.2个 D.1个或2个
答案 D ∵直线y=x+a不经过第二象限,∴a≤0.当a=0时,方程为2x+1=0,只有一个实数解;当a<0时,方程ax2+2x+1=0为一元二次方程,Δ=4-4a>0,∴方程有两个解.故方程有1个解或2个解.故选D.
易错警示 本题易将a=0的情况漏掉,从而错选C.
2.(2019山东潍坊,12,3分)抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3-t=0(t为 实数)在-1
思路分析 根据所给的抛物线的对称轴求出函数解析式为y=x2-2x+3,将一元二次方程x2+2x+3-t=0有实 数根看作y=x2-2x+3的图象与直线y=t有交点,再由-1
答案 D 不妨设c>0.一段抛物线L:y=-x(x-3)+c(0≤x≤3)可以看作抛物线y=-x(x-3)(0≤x≤3)沿y轴向上 平移c个单位形成的,一段抛物线L:y=-x(x-3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点可以看作直线l:y=x+ 2沿y轴向下平移c个单位形成的直线y=x+2-c与抛物线y=-x(x-3)(0≤x≤3)有唯一公共点.当直线y=x+2-c (即l2)经过原点时,0+2-c=0,c=2;当直线y=x+2-c(即l3)经过点A(3,0)时,3+2-c=0,c=5,根据图象可得当2
5.(2020湖北武汉,15,3分)抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过A(2,0),B(-4,0)两点.下列四个结论:①一元二次方程ax2+bx+c=0的根为x1=2,x2=-4;②若点C(-5,y1),D(π,y2)在该抛物线上,则y1
解题关键 抓住抛物线的对称性和对称轴方程是判断正误的关键.
6.(2019山东潍坊,17,3分)如图,直线y=x+1与抛物线y=x2-4x+5交于A,B两点,点P是y轴上的一个动点,当△ PAB的周长最小时,S△PAB= .
解析 联立直线与抛物线的解析式得方程组 解得 或 ∴点A的坐标为(1,2),点B的坐标为(4,5),∴AB= =3 ,作点A关于y轴的对称点A',则A'(-1,2),连接A'B与y轴交于P',则当点P与P'重合时,△PAB的周长最小, 设直线A'B的解析式为y=kx+b,k≠0,
则 解得 ∴直线A'B的解析式为y= x+ ,当x=0时,y= ,即点P'的坐标为 ,将x=0代入y=x+1中,得y=1,∵直线y=x+1与y轴的夹角是45°,∴点P'到直线AB的距离是 ×sin 45°= × = ,∴△P'AB的面积是 = .∴当△PAB的周长最小时,S△PAB= .
7.(2018湖北黄冈,22,8分)已知直线l:y=kx+1与抛物线y=x2-4x.(1)求证:直线l与该抛物线总有两个交点;(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
8.(2019北京,26,6分)在平面直角坐标系xOy中,抛物线y=ax2+bx- 与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点P ,Q(2,2).若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
解析 (1)∵抛物线y=ax2+bx- 与y轴交于点A,∴点A的坐标为 .∵将点A向右平移2个单位长度,得到点B,∴点B的坐标为 .(2)∵点B 在抛物线上,∴4a+2b- =- ,即b=-2a.∴抛物线的对称轴为直线x=1.(3)点A ,B ,P .
当a>0时,- <0,如图1. 图1设抛物线上的点C .∵当x<1时,y随x的增大而减小,∴yC<- .设抛物线上的点D(xD,2)(xD>1).∵当x>1时,y随x的增大而增大,∴xD>2.
结合函数图象,可知抛物线与线段PQ没有公共点.当a<0时,(i)当-
设抛物线上的点D(xD,2)(xD>1).∵当x>1时,y随着x的增大而减小,∴xD>2.结合函数图象,可知抛物线与线段PQ没有公共点.(ii)当a=- 时,A(0,2),B(2,2),P ,Q(2,2),如图3. 图3结合函数图象,可知抛物线与线段PQ恰有一个公共点Q(2,2).
(iii)当a<- 时,0<- <2,如图4. 图4设抛物线上的点C .∵当x<1时,y随x的增大而增大,∴yC>- .设抛物线上的点D(xD,yD) ,
∵当x>1时,y随x的增大而减小,∴xD<2.结合函数图象,可知抛物线与线段PQ恰有一个公共点.综上所述,a的取值范围为a≤- .
解题关键 解决本题的关键是分情况讨论后精准画图,要在探究的过程中发现点P与点A,B纵坐标相等 的关系,进而关注点Q与抛物线的位置关系.
9.(2019安徽,22,12分)一次函数y=kx+4与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是 该二次函数图象的顶点.(1)求k,a,c的值;(2)过点A(0,m)(0
1.(2020广西崇左江州一模,10)若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-m的图象上的三点,则y1,y2,y3 的大小关系是 ( )A.y1
2.(2020海南琼海一模,7)抛物线y=(x-1)2+3关于x轴对称的抛物线的解析式是 ( )A.y=-(x-1)2+3 B.y=(x+1)2+3C.y=(x-1)2-3 D.y=-(x-1)2-3
答案 D ∵抛物线y=(x-1)2+3的顶点坐标为(1,3),∴此抛物线关于x轴对称的抛物线的顶点坐标为(1,-3),且开口向下,∴所求抛物线解析式为y=-(x-1)2-3.故选D.
3.(2020湖北荆州4月模拟,9)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+ac的图象不经过 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限
4.(2019四川绵阳涪城二诊,6)若抛物线y=x2-6x+m与x轴没有交点,则m的取值范围是 ( )A.m>9 B.m≥9 C.m<-9 D.m≤-9
答案 A ∵抛物线y=x2-6x+m与x轴没有交点,∴Δ=b2-4ac<0,即(-6)2-4×1×m<0,解得m>9,∴m的取值范围 是m>9.故选A.
二、填空题(每小题3分,共12分)5.(2020上海长宁二模,11)如果抛物线y=(a-1)x2-1(a为常数)不经过第二象限,那么a的取值范围是 .
解析 ∵抛物线y=(a-1)x2-1(a为常数)不经过第二象限,且该抛物线交y轴于负半轴,∴a-1<0,解得a<1.
6.(2020吉林长春一模,14)如图,在平面直角坐标系中,抛物线y=a(x+1)2+b与y=a(x-2)2+b+1交于点A.过点A 作y轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为 .
解析 设抛物线y=a(x+1)2+b的对称轴与线段BC交于点E,抛物线y=a(x-2)2+b+1的对称轴与线段BC交于 点F,如图所示. 可知抛物线y=a(x+1)2+b的对称轴为直线x=-1,抛物线y=a(x-2)2+b+1的对称轴为直线x=2.由抛物线的对称性可知BE=AE,CF=AF,∴BC=BE+AE+AF+CF=2(AE+AF)=2×[2-(-1)]=6.
7.(2018上海宝山一模,15)二次函数y=- (x-1)2+ 的图象与y轴的交点坐标是 .
8.(2019四川成都龙泉驿二诊,12)将二次函数y=x2的图象先向上平移1个单位,然后向右平移2个单位,得到 新的二次函数的顶点式为 .
答案 y=(x-2)2+1
解析 将抛物线y=x2先向上平移1个单位,然后向右平移2个单位,得到的抛物线的表达式为y=(x-2)2+1.
三、解答题(共31分)9.(2020上海静安一模,24)在平面直角坐标系xOy中(如图),已知二次函数y=ax2+bx+c(其中a、b、c是常数, 且a≠0)的图象经过点A(0,-3)、B(1,0)、C(3,0),连接AB、AC.(1)求这个二次函数的解析式;(2)点D是线段AC上的一点,连接BD,如果S△ABD∶S△BCD=3∶2,求tan∠DBC的值;(3)如果点E在该二次函数图象的对称轴上,当AC平分∠BAE时,求点E的坐标.
(2)过点D作DH⊥BC于H.在△ABC中,设AC边上的高为h,则 = = = .由作图知DH∥y轴,∴△CHD∽△COA,∴ = = = .∵OA=OC=3,∴CH=DH= ×3= ,∴BH=BC-CH=2- = ,∴tan∠DBC= = .(3)∵y=-x2+4x-3=-(x-2)2+1,∴抛物线的对称轴为直线x=2,设直线x=2与x轴交于点G,过点A作AF垂直于直线x=2,垂足为F.
∵OA=OC=3,∠AOC=90°,∴∠OAC=∠OCA=45°.易知AF∥x轴,∴∠FAC=∠OCA=45°.∵AC平分∠BAE,∴∠BAC=∠EAC.∵∠BAO=∠OAC-∠BAC,∠EAF=∠FAC-∠EAC,∴∠BAO=∠EAF.又∵∠AOB=∠AFE=90°,∴△OAB∽△FAE,∴ = = .∵AF=2,∴EF= ,∴EG=GF-EF=AO-EF=3- = ,∴E点坐标为 .
10.(2020上海奉贤二模,24)如图,在平面直角坐标系xOy中,抛物线y=x2+bx经过点A(2,0).直线y= x-2与x轴交于点B,与y轴交于点C.(1)求这条抛物线的表达式和顶点的坐标;(2)将抛物线y=x2+bx向右平移,使平移后的抛物线经过点B,求平移后抛物线的表达式;(3)将抛物线y=x2+bx向下平移,使平移后的抛物线交y轴于点D,交线段BC于点P、Q(点P在点Q右侧),平移 后抛物线的顶点为M,连接MC,如果DP∥x轴,求∠MCP的正弦值.
解析 (1)由抛物线y=x2+bx经过点A(2,0),得0=4+2b,解得b=-2,∴抛物线的表达式是y=x2-2x.∵y=x2-2x=(x-1)2-1,∴抛物线的顶点坐标是(1,-1).(2)∵直线y= x-2与x轴交于点B,∴令y=0,得x=4,∴点B的坐标是(4,0).①将抛物线y=x2-2x向右平移2个单位长度,使得点A移动到点B,此时平移后的抛物线的表达式是y=(x-3)2- 1.②将抛物线y=x2-2x向右平移4个单位长度,使得点O移动到点B,此时平移后的抛物线的表达式是y=(x-5)2- 1.
(3)如图,设向下平移后的抛物线的表达式是y=x2-2x+n,则点D(0,n).∵DP∥x轴,∴点D、P关于抛物线的对称轴x=1对称,∴P(2,n).∵点P在直线BC上,∴n= ×2-2=-1.∴平移后的抛物线的表达式是y=x2-2x-1.∴新抛物线的顶点M的坐标是(1,-2).由C为直线y= x-2与y轴的交点可得C(0,-2),∴MC∥OB,∴∠MCP=∠OBC.在Rt△OBC中,sin∠OBC= ,∵OC=2,OB=4,∴BC=2 ,
∴sin∠MCP=sin∠OBC= = ,即∠MCP的正弦值是 .
11.(2019云南昆明盘龙一模,20)如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴 为直线x=2.(1)求抛物线的函数表达式;(2)根据图象,直接写出不等式x2+bx+c>0的解集;(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为 .
解析 (1)∵AB=2,抛物线的对称轴为直线x=2,∴点A的坐标是(1,0),点B的坐标是(3,0).把A、B两点的坐标代入抛物线解析式得 解得 ∴抛物线的函数表达式为y=x2-4x+3.(2)不等式x2+bx+c>0即y>0,由题图及(1)得x<1或x>3.故不等式x2+bx+c>0的解集为x<1或x>3.(3)y=x2-4x+3=(x-2)2-1,∴顶点坐标为(2,-1).易知点D,E不可能都在x轴下方.当点E,D均在x轴的上方时,由题意得DE∥AB,AD=AB=BE=DE=2,由抛物线的对称性,不妨设点D在对称 轴左侧,设对称轴与x轴的交点为G,则EG= = ,∴E(2, ).由DE=2得D的坐标为(0, ).当x=0时,y=02-4×0+3=3≠ ,故此时点D不在抛物线上,不合题意.
当点D,E位于x轴两侧时,如图,根据“菱形的对角线互相垂直平分,抛物线的对称性”得点D是抛物线y=x 2-4x+3的顶点,即D(2,-1),故答案是(2,-1).
B组 2018—2020年模拟·提升题组时间:45分钟 分值:50分一、选择题(每小题3分,共12分)1.(2020江西南昌一模,6)对于二次函数y=ax2+(1-2a)x(a>0),下列说法错误的是 ( )A.该二次函数图象的对称轴可以是y轴B.该二次函数图象的对称轴不可能是直线x=1C.当x>2时,y随x的增大而增大D.该二次函数图象的对称轴只能在y轴的右侧
2.(2018湖北黄石模拟,8)若a<0,b>0,c<0,则二次函数y=ax2+bx+c的大致图象为 ( )
3.(2020辽宁大连金州一模,10)如图,抛物线y=x2+2x-3与x轴相交于A、B两点(点A位于点B左侧),与y轴相 交于点C,点D在抛物线上,且CD∥AB,BD与y轴相交于点E,过点E的直线FG平行于x轴,与抛物线交于F,G 两点(点F位于点G左侧),则线段FG的长为 ( ) A.1+ B.3 C.2 D.2+
答案 C y=x2+2x-3=(x+3)(x-1).令x=0,得y=-3,∴C(0,-3).令y=0,则(x+3)(x-1)=0,∴x=-3或1,∴B(1,0).∵y=x2+2x-3=(x+1)2-4,∴抛物线对称轴为直线x=-1.∵CD∥AB,∴C、D两点关于直线x=-1对称,∴D(-2,-3).设直线BD的解析式为y=mx+n(m≠0),则 解得 ∴直线BD的解析式为y=x-1,∴E(0,-1).令x2+2x-3=-1,解得x1,2=-1± ,∴F(-1- ,-1),G(-1+ ,-1),∴FG=(-1+ )-(-1- )=2 ,故选C.
4.(2019辽宁鞍山铁西三模,7)二次函数y=ax2+bx+c(a、b、c为常数且a≠0)的x与y的部分对应值如下表:
给出如下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为-3;(2)当-
二、填空题(每小题3分,共9分)5.(2020上海宝山二模,13)若抛物线y=(x-m)2+(m+1)的顶点在第二象限,则m的取值范围为 .
解析 ∵y=(x-m)2+(m+1),∴顶点坐标为(m,m+1).∵顶点在第二象限,∴m<0,m+1>0,∴-1
7.(2020辽宁鞍山铁东一模,16)已知二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=-1,图象如图所示, 下列结论:①abc>0;②b2-4ac>0;③4a+c>0;④若t为任意实数,则有a-bt≤at2+b;⑤当图象经过点(1,2)时,若方 程ax2+bx+c-2=0的两实根为x1,x2(x1
三、解答题(共29分)8.(2020上海青浦二模,24)如图,在平面直角坐标系xOy中,二次函数y=ax2-4ax+3的图象与x轴正半轴交于 点A、B,与y轴相交于点C,顶点为D,且tan∠CAO=3.(1)求这个二次函数的解析式;(2)点P是对称轴右侧抛物线上的点,连接CP,交对称轴于点F,当S△CDF∶S△FDP=2∶3时,求点P的坐标;(3)在(2)的条件下,将△PCD沿直线MN翻折,当点P恰好与点O重合时,折痕MN交x轴于点M,交y轴于点N, 求 的值.
解析 (1)在y=ax2-4ax+3中,令x=0,得y=3,∴点C的坐标为(0,3),∴OC=3.在Rt△AOC中,tan∠CAO= =3,∴OA=1.∴A(1,0).将点A的坐标代入y=ax2-4ax+3,得a-4a+3=0,解得a=1.∴二次函数的解析式为y=x2-4x+3.(2)如图,过点C作CG⊥DF,过点P作PQ⊥DF,垂足分别为点G、Q.
∵抛物线y=x2-4x+3=(x-2)2-1的对称轴为直线x=2,∴CG=2,∵ = = ,∴PQ=3,∴点P的横坐标为5,把x=5代入y=x2-4x+3,得y=8,∴点P的坐标为(5,8).(3)如图,连接OP,过点P作PH⊥x轴于点H. ∵点P的坐标为(5,8),∴OH=5,PH=8,∵将△PCD沿直线MN翻折,点P恰好与点O重合,∴MN⊥OP,∴∠ONM+∠NOP=90°.
又∵∠POH+∠NOP=90°,∴∠ONM=∠POH,∴tan∠ONM= =tan∠POH= = .
9.(2019云南昆明西山一模,21)如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中A 点的坐标为(-3,0),C为抛物线与y轴的交点.(1)求抛物线的解析式;(2)若点P在抛物线上,且S△POC=2S△BOC,求点P的坐标.
解析 (1)∵抛物线的对称轴为直线x=-1,A点的坐标为(-3,0),∴点B的坐标为(1,0).将点A和点B的坐标代入抛物线的解析式得 解得b=2,c=-3,∴抛物线的解析式为y=x2+2x-3.(2)将x=0代入y=x2+2x-3,得y=-3,∴点C(0,-3),OC=3.∵点B的坐标为(1,0),∴OB=1.设点P的坐标为(a,a2+2a-3),则点P到OC的距离为|a|.∵S△POC=2S△BOC,∴ OC·|a|=2× OC·OB,即 ×3×|a|=2× ×3×1,解得a=±2.
当a=2时,点P的坐标为(2,5);当a=-2时,点P的坐标为(-2,-3).∴点P的坐标为(2,5)或(-2,-3).
10.(2020广东广州一模,24)如图,已知顶点为C(0,-3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+ m过顶点C和点B.(1)求m的值;(2)求函数y=ax2+b(a≠0)的解析式;(3)抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.
解析 (1)将(0,-3)代入y=x+m,可得m=-3.(2)将y=0代入y=x-3,得x=3,∴点B的坐标为(3,0),将(0,-3),(3,0)分别代入y=ax2+b,得 解得 ∴二次函数的解析式为y= x2-3.(3)存在,分以下两种情况:
①若M在B上方,设MC交x轴于点D,则∠ODC=∠OBC+∠MCB=45°+15°=60°,∴OD=OC·tan 30°= ,∴D( ,0).设直线DC的解析式为y=k1x-3(k≠0),将( ,0)代入y=k1x-3,可得k1= .∴直线DC的解析式为y= x-3.由 解得 或 ∴M1(3 ,6).②若M在B下方,设MC交x轴于点E,则∠OCE=45°+15°=60°,∴OE=OC·tan 60°=3 .设直线EC的解析式为y=k2x-3(k≠0),将(3 ,0)代入y=k2x-3,可得k2= .∴直线EC的解析式为y= x-3.
2021年全国中考数学真题分类汇编--函数:二次函数(试卷版): 这是一份2021年全国中考数学真题分类汇编--函数:二次函数(试卷版),共17页。
2021版《5年中考3年模拟》全国版中考数学:21版53中考全国数学教参目录: 这是一份2021版《5年中考3年模拟》全国版中考数学:21版53中考全国数学教参目录,共2页。
2021版《5年中考3年模拟》全国版中考数学:§3.5 二次函数的综合应用: 这是一份2021版《5年中考3年模拟》全国版中考数学:§3.5 二次函数的综合应用,共60页。












