2021版《5年中考3年模拟》全国版中考数学：§6.1　图形的轴对称、平移与旋转

这是一份2021版《5年中考3年模拟》全国版中考数学：§6.1　图形的轴对称、平移与旋转，共60页。
1.(2020山西,2,3分)自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科 学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是 (　　) 
答案    D    根据轴对称图形的定义知只有D选项正确,故选D.
2.(2019湖北武汉,4,3分)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字 是轴对称图形的是(　　) 诚　信　友　善 A　     B　　    C　　    D
答案    D　选项A、B、C中的图形都不是轴对称图形,选项D中的图形是轴对称图形.故选D.
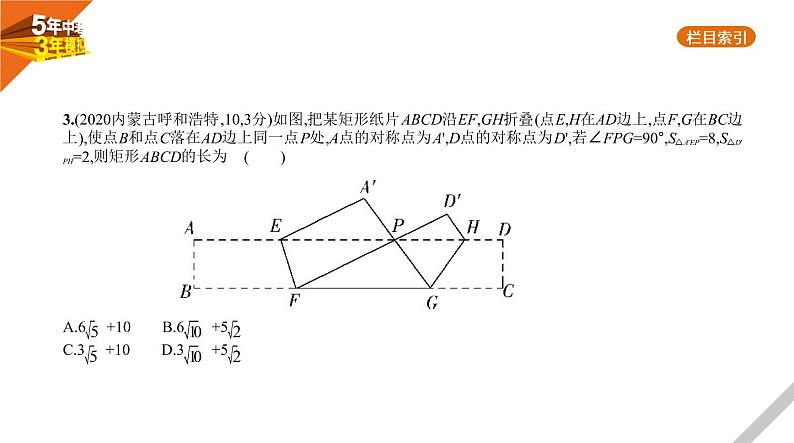
3.(2020内蒙古呼和浩特,10,3分)如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边 上),使点B和点C落在AD边上同一点P处,A点的对称点为A',D点的对称点为D',若∠FPG=90°,S△A'EP=8,S△D' PH=2,则矩形ABCD的长为 (　　) A.6 +10　    B.6 +5 　    C.3 +10　    D.3 +5 
答案    D　由折叠可得,∠A'PF=∠B=90°,∠D'PG=∠C=90°,∵∠FPG=90°,∴∠A'PD'=90°,∴∠A'PE+∠D'PH=∠A'PE+∠A'EP=90°,∴∠A'EP=∠D'PH,又∵∠A'=∠D'=90°,∴△A'EP∽△D'PH,∵四边形ABCD是矩形,∴AB=CD,AD=BC,设AB=CD=x(x>0),由折叠可知PA'=AB=x,PD'=CD=x,∵△A'EP的面积为8,△D'PH的面积为2,且△A'EP∽△D'PH,∴A'P∶D'H=2,∵PA'=x,∴D'H= x,∵S△D'PH= ·x· x=2,
∴x=2 (舍去负根).∴AB=CD=2 ,∴A'E=4 ,D'H= ,∴PE= =2 ,PH= = ,∴AD=4 +2 + + =5 +3 .
方法指导　在翻折过程中,注意等量关系,运用多种性质、定理,从等量关系中寻找相似或全等,利用参数 解决问题.
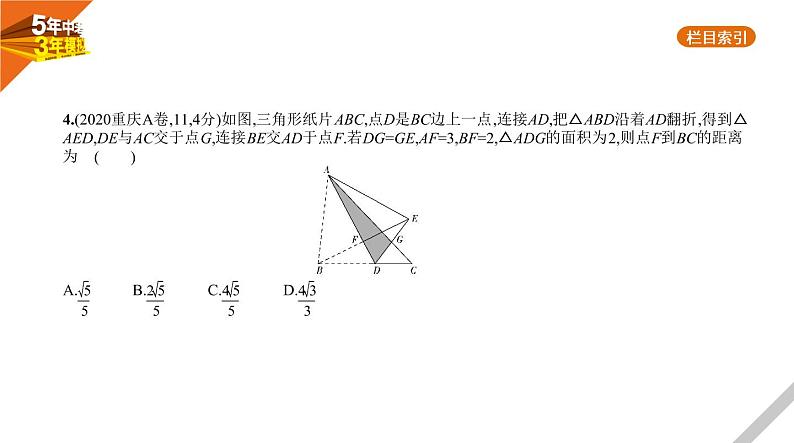
4.(2020重庆A卷,11,4分)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△ AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC的距离 为 (　　) A. 　    B. 　    C. 　    D. 
答案    B　由翻折得BF=EF=2,∠AFB=∠AFE=90°,因为△ADG的面积为2,DG=GE,所以△AGE的面积为 2,所以△ADE的面积为4,所以 AD·EF=4,所以AD=4,所以DF=AD-AF=4-3=1,所以BD= = = ,设点F到BC的距离是h,则S△BDF= DF·BF= BD·h,即1×2= h,所以h= ,即点F到BC的距离为 .
方法总结　求点到直线的距离时,等面积法是一个常用方法.特别是求直角三角形斜边上的高.
5.(2019吉林,12,3分)如图,在四边形ABCD中,AB=10,BD⊥AD.若将△BCD沿BD折叠,点C与边AB的中点E 恰好重合,则四边形BCDE的周长为　　　    . 
解析　根据折叠的性质和E为AB的中点可知,BC=BE=5,CD=DE.∵BD⊥AD,∴CD=DE=5.∴四边形 BCDE的周长为20.
6.(2020四川成都,27,10分)在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上 点F处.(1)如图1,若BC=2BA,求∠CBE的度数;(2)如图2,当AB=5,且AF·FD=10时,求BC的长;(3)如图3,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD时,求 的值. 
解析　(1)由翻折可知BC=BF,∠EBC=∠EBF,∵BC=2BA,∴BF=2AB,又∠A=90°,∴∠AFB=30°,∵AD∥BC,∴∠FBC=∠AFB=30°,∴∠CBE= ∠FBC=15°.(2)由翻折可知BC=BF,∠BFE=∠C=90°,易知△ABF∽△DFE,∴ = ,∴AF·DF=AB·DE.∵AF·DF=10,AB=5,∴DE=2,∴FE=CE=3,∴DF= = ,∴AF=2 .
∴BC=AD=AF+DF=3 .(3)过点N作NG⊥BF于点G,∵BN平分∠ABF,NA⊥BA,∴AN=NG.∵∠NGF=∠A=90°,∠AFB=∠GFN,∴△NFG∽△BFA,∵NF=AN+FD,∴NF= AD= BC= BF,∴ = = = ,∴NG=AN= AB,在Rt△ABF中,AB2+AF2=BF2,∴AB2+ =BC2,化简得5AB2+2AB·BC-3BC2=0,解得 =  .
方法总结　①解决矩形的折叠问题,要注意折叠前后图形间的全等关系及平行线间的内错角相等.②求 长度或比值问题,要注意寻找与所求线段或已知线段有关的相似三角形.③几何证明题中要先注意 “K”“X”“A”型的相似三角形的相似比,再进行线段的等量代换.
7.(2019山西,22,11分)动手操作:第一步:如图1,正方形纸片ABCD沿对角线AC所在的直线折叠,展开铺平.再沿过点C的直线折叠,使点B, 点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一条直线上,折痕分别为 CE,CF,如图2.第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3.第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5.图中的虚 线为折痕.问题解决:(1)在图5中,∠BEC的度数是　　　    , 的值是　　　    ;(2)在图5中,请判断四边形EMGF的形状,并说明理由;(3)在不增加字母的条件下,请你以图5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写 出这个菱形:　　　    .
解析　(1)67.5°; . (4分)(2)四边形EMGF是矩形. (5分)理由如下:∵四边形ABCD是正方形,∴∠B=∠BCD=∠D=90°.由折叠可知,∠1=∠2=∠3=∠4,CM=CG,∠BEC=∠NEC=∠NFC=∠DFC,∴∠1=∠2=∠3=∠4= =22.5°.∴∠BEC=∠NEC=∠NFC=∠DFC=67.5°.由折叠可知,MH,GH分别垂直平分EC,FC,∴MC=ME,GC=GF.∴∠5=∠1=22.5°,∠6=∠4=22.5°,∴∠MEF=∠GFE=90°. (7分)∵∠MCG=90°,CM=CG,∴∠CMG=45°.
又∵∠BME=∠1+∠5=45°,∴∠EMG=180°-∠CMG-∠BME=90°. (8分)∴四边形EMGF是矩形. (9分) (3)答案不唯一,画出正确图形(一个即可). (10分)菱形FGCH(或菱形EMCH). (11分) 　     
解后反思　折叠的性质:①位于折痕两侧的图形关于折痕对称;②折叠前后的两部分图形全等,对应边、 角、线段、周长、面积等均相等;③折叠之后,对应点的连线被折痕垂直平分.
1.(2020河南,9,3分)如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正 方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为 (　　) A. 　    B.(2,2)　    C. 　    D.(4,2)
答案    B　∵A(-2,6),∴OC=2,AC=6,∴正方形OCDE的边长为2,∵B(7,0),∴OB=7,∴BC=9,如图,当点E'在AB边上时,易证Rt△E'O'B∽Rt△ACB,∴ = ,∴O'B= ×2=3,∴OC'=OB-O'B-O'C'=7-3-2=2,∴点D'的坐标为(2,2).即当点E落在AB边上时,点D的坐标为(2,2).故选B. 
思路分析　根据题意作出平移后的正方形O'C'D'E',依据条件证得Rt△E'O'B∽Rt△ACB,由相似的性质 得O'B的长,进而求出D'的坐标,即平移后点D的坐标.
2.(2020广东广州,14,3分)如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移到△ECD,若四边 形ABDC的面积为9,则点C的坐标为　　　    . 
解析　∵△CED由△AOB向右平移所得,点A的坐标为(1,3),∴点C的纵坐标为3.易知四边形ABDC为平行四边形,∴S四边形ABDC=3BD=9,∴BD=3,∴AC=BD=3.∴点C的坐标为(4,3).
解题关键　能根据已知条件求出AC的长度是解题的关键.
1.(2019辽宁大连,6,3分)下列所述图形中,既是轴对称图形又是中心对称图形的是 (　　)A.等腰三角形　    B.等边三角形C.菱形　     D.平行四边形
答案    C　根据轴对称图形的定义可得等腰三角形、等边三角形、菱形是轴对称图形,根据中心对称图 形的定义可得菱形、平行四边形是中心对称图形,所以既是轴对称图形又是中心对称图形的只有菱形. 故选C.
2.(2020海南,7,3分)如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到 Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是 (　　) A.1 cm　　B.2 cm　　C.  cm　　D.2  cm
答案    B　∵∠C=90°,∠ABC=30°,AC=1 cm,∴∠BAC=60°,AB=2 cm.由旋转的性质可得∠BAC=∠BAB'= 60°,AB=AB'.所以△ABB'是等边三角形.∴BB'=AB=2 cm.故选B.
解题关键　解决本题的关键在于根据旋转的性质得出△ABB'是等边三角形.
3.(2020宁夏,13,3分)如图,直线y= x+4与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转90°后得到△A1O1B,则点A1的坐标是　　　    . 
4.(2019湖北武汉,16,3分)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P, 可推出结论:PA+PC=PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=4 .点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是　　　    . 　      　图1　　　　　　　　　　图2
5.(2019山西,15,3分)如图,在△ABC中,∠BAC=90°,AB=AC=10 cm,点D为△ABC内一点,∠BAD=15°,AD=6 cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于 点F,则CF的长为　　　    cm. 
解析　过点A作AG⊥DE于点G. 由旋转的性质知AD=AE,∠DAE=90°,∠CAE=∠BAD=15°,∴∠AED=45°,∴∠AFD=∠AED+∠CAE=60°,在Rt△ADG中,AG=DG= =3 ,在Rt△AFG中,GF= = ,AF=2FG=2 ,
∴CF=AC-AF=10-2 .故CF的长为(10-2 )cm.
6.(2020内蒙古包头,25,12分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,Rt△ABC绕点C按顺时针方向 旋转得到Rt△A'B'C,A'C与AB交于点D.(1)如图1,当A'B'∥AC时,过点B作BE⊥A'C,垂足为E,连接AE.①求证:AD=BD;②求 的值;(2)如图2,当A‘C⊥AB时,过点D作DM∥A’B‘,交B’C于点N,交AC的延长线于点M,求 的值. 图1 图2
解析　(1)①证明:∵A'B'∥AC,∴∠B'A'C=∠A'CA.∵∠B'A'C=∠BAC,∴∠A'CA=∠BAC,∴AD=CD.∵∠A'CA+∠BCD=90°,∠BAC+∠ABC=90°,∴∠BCD=∠ABC,∴CD=BD,∴AD=BD. (3分)②在Rt△ABC中,∵BC=2,AC=4,∴AB=2 .∵BE⊥A'C,∴∠BEC=90°,在Rt△BEC和Rt△ACB中,∵∠BCE=∠ABC,∴tan∠BCE=tan∠ABC,∴ = =2,∴BE=2CE.在Rt△BEC中,∵BE2+CE2=BC2,∴(2CE)2+CE2=4,∴CE= .∵CD= AB,∴CD= ,∴DE=CD-CE= ,
∴ = = .∵AD=BD,∴S△ADE=S△BDE,∴S△ABE=2S△ADE,∴ = = . (8分)(2)∵A'C⊥AB,∴∠NCD=∠BDC=90°.∵DM∥A'B',∴∠DNC=∠A'B'C=∠ABC.∵DC=CD,∴△NCD≌△BDC,∴NC=BD,DN=CB=2.∵∠BCD+∠ABC=90°,∠BAC+∠ABC=90°,∴∠BCD=∠BAC.在Rt△CDB和Rt△ACB中,∵tan∠BCD=tan∠BAC,∴ = .∵S△ABC= AB·CD= AC·BC,∴CD= ,
∴BD= ,∴CN= ,AD= .∵∠NCD=∠BDC=90°,∴CN∥AB,∴∠NCM=∠BAC.∵∠NMC=∠DMA,∴△MNC∽△MDA,∴ = ,∴ = ,∴MN= ,∴ =3. (12分)
1.(2020重庆A卷,2,4分)下列图形是轴对称图形的是 (　　) 
答案    A　根据轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个 图形叫做轴对称图形,可知选项A中的图形是轴对称图形.故选A.
2.(2020湖北武汉,4,3分)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是 轴对称图形的是 (　　) 
答案    C　只有C能找到对称轴,是轴对称图形.故选C.
3.(2019天津,4,3分)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的 是 (　　) 
答案    A　根据轴对称图形的概念可得选项B、C、D都不是轴对称图形,“美”可以看作轴对称图形. 故选A.
4.(2019北京,2,2分)下列倡导节约的图案中,是轴对称图形的是(　　) 
答案    C　选项A、B、D不是轴对称图形,选项C是轴对称图形.故选C.
5.(2020湖北武汉,16,3分)如图,折叠矩形纸片ABCD,使点D落在AB边的点M处,EF为折痕,AB=1,AD=2.设 AM的长为t,用含有t的式子表示四边形CDEF的面积是　　　    . 
解析　如图,设MN与BC的交点为P,AE=x,由折叠性质可得CF=FN,CD=MN=1,∠EMN=90°,DE=EM=2-x, 再由矩形ABCD可得∠AME=∠MPB,∵AM=t,∴MB=1-t,在Rt△AEM中,AE2+AM2=EM2,即x2+t2=(2-x)2,解得 x= ,则DE=2-x= ,sin∠AME= = ,tan∠AME= = ,在Rt△MPB中,MP= = = ,∴NP=1-MP= ,∵∠FPN=∠MPB,∠MPB=∠AME,∴FN=NPtan∠AME= ,∴CF= ,∴四边形CDEF的面积为 ×CD=  = t2- t+1. 
难点突破　设MN与BC的交点为P,求出AE,并利用∠AME=∠MPB=∠FPN及锐角三角函数求出NF是解 答本题的突破口.
6.(2020新疆,15,5分)如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小 值为　　　    . 
解后反思　此题主要考查了利用特殊角的三角函数求线段长以及线段和的最值问题,难度较大.如何将  DC转化为DF的长是难点,充分利用含30°角的直角三角形的性质,将AD+ DC转化为AD+DF,然后利用“垂线段最短”的性质巧妙解决.
一题多解　如图所示,作点A关于BC的对称点A',连接AA'交BC于点H,连接A'D,过D作DE⊥AC于E.在Rt△ABH中,∠B=60°,AB=2,∴AH= ,∴AA'=2 ,在Rt△CDE中,DE= CD,即2DE=DC,∴2AD+DC=2(AD+DE).∵A与A'关于BC对称,∴AD=A'D,∴AD+DE=A'D+DE,∴当A',D,E在同一直线上时,AD+DE的最小值等于A'E的长,在Rt△AA'E中,A'E=sin 60°·AA'= ×2 =3,∴AD+DE的最小值为3,即2AD+DC的最小值为6,故答案为6.
7.(2019河南,15,3分)如图,在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE= a.连接AE,将△ABE沿AE折叠,若点B的对应点B'落在矩形ABCD的边上,则a的值为　　　    . 
解析　在矩形ABCD中,AB=CD=1,AD=BC=a,∠B=∠C=∠D=90°,由折叠得B'E=BE= a,∠AB'E=90°.①当点B'落在边AD上时,易证四边形ABEB'是正方形,∴BE=AB,即 a=1,a= ; ②当点B'落在边CD上时,如图. 
∵∠1+∠2=∠2+∠3=90°,∴∠1=∠3,又∠D=∠C=90°,∴△B'CE∽△ADB',∴ = .在Rt△ADB'中,由勾股定理得B'D= = ,∴ = ,∴a= (负值舍去).综上所述,满足条件的a的值为 或 .
解题关键　本题是以矩形为背景的折叠型题目,由于未指明折叠后点B'的具体位置,所以分情况讨论是 解决本题的关键.根据题意得,当点B'在矩形边上时,有两种可能:①当点B'在AD上时,由四边形ABEB'是正 方形可求a的值;②当点B'在边CD上时,由“K字模型”中的相似三角形性质结合勾股定理可求a的值.
8.(2019山东潍坊,16,3分)如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A',折痕为DE.若 将∠B沿EA'向内翻折,点B恰好落在DE上,记为B',则AB=　　　    . 
9.(2019广东广州,24,14分)如图,等边△ABC中,AB=6,点D在BC上,BD=4.点E为边AC上一动点(不与点C重 合),△CDE关于DE对称的图形为△FDE.(1)当点F在AC上时,求证:DF∥AB;(2)设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存 在,请说明理由;(3)当B,F,E三点共线时,求AE的长.
解析　(1)证明:∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,由△CDE关于DE对称的图形为△FDE可知DF=DC,又点F在AC上,∴∠DFC=∠C=60°,∴∠DFC=∠A,∴DF∥AB.(2)存在.如图,过点D作DM⊥AB,交AB于点M. ∵BC=AB=6,BD=4,∴CD=2,∴DF=2,∴点F在以D为圆心,DF为半径的圆上,
∴当点F在DM上时,S2最小,∵BD=4,DM⊥AB,∠ABC=60°,∴MD=2 ,∴S2的最小值= ×6×(2 -2)=6 -6,∵S1= ×2×3 =3 ,∴S最大值=3 -(6 -6)=6-3 .
(3)如图,过点D作DG⊥EF于点G,过点E作EH⊥CD于点H.∵△CDE关于DE对称的图形为△FDE,∴DF=DC=2,∠EFD=∠C=60°,∵GD⊥EF,∴FG=1,DG= .∵BD2=BG2+DG2,∴16=BG2+3,
∴BG= ,∵EH⊥BC,∠C=60°,∴CH= ,EH= EC,∵∠GBD=∠EBH,∠BGD=∠BHE=90°,∴△BGD∽△BHE,∴ = ,∴ = ,∴EC= -1,∴AE=AC-EC=7- .
思路分析　(1)由对称的性质和等边三角形的性质可得∠DFC=∠A,可证DF∥AB.(2)过点D作DM⊥AB,交AB于点M,由题意可得点F在以D为圆心,DF为半径的圆上,由△ACD的面积S1的 值是定值,可得当点F在DM上时,S△ABF最小,S最大.(3)过点D作DG⊥EF于点G,过点E作EH⊥CD于点H,由勾股定理可求BG的长,通过证明△BGD∽△BHE, 可求EC的长,即可求AE的长.
1.(2019江苏苏州,9,3分)如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16.将△ABO沿点A到点C的 方向平移,得到△A'B'O'.当点A'与点C重合时,点A与点B'之间的距离为 (　　) A.6　    B.8　    C.10　    D.12
解后反思　本题考查了菱形的对角线互相垂直平分及图形平移的性质,可通过构造直角三角形,运用勾 股定理求得AB'的长.
2.(2019安徽,16,8分)如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了以格点(网格线 的交点)为端点的线段AB.(1)将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD;(2)以线段CD为一边,作一个菱形CDEF,且点E,F也为格点.(作出一个菱形即可) 
解析　(1)如图,线段CD即为所求作的图形. (4分)(2)如图,菱形CDEF即为所求作的图形(答案不唯一). (8分) 
1.(2020广西北部湾经济区,2,3分)下列图形是中心对称图形的是     (　　) 
答案    D　根据中心对称图形的定义,可知A、B、C不是中心对称图形,D是中心对称图形.故选D.
2.(2019吉林,4,2分)把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度 至少为 (　　)A.30°　    B.90°　    C.120°　    D.180°
答案    C　图形中有三个箭头,所以与自身重合的旋转角度至少为360°÷3=120°.故选C.
3.(2019黑龙江齐齐哈尔,2,3分)下面四个图形中,既是轴对称图形又是中心对称图形的是 (　　) 
答案    D    A和B中图形均是中心对称图形,不是轴对称图形.C中图形是轴对称图形,不是中心对称图形. D中图形既是轴对称图形,又是中心对称图形.故选D.
4.(2020黑龙江齐齐哈尔,9,3分)有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先 将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图②所示,则旋转角 ∠BAD的度数为 (　　) A.15°　    B.30°　    C.45°　    D.60°
答案    B　如图所示,由题意得∠B=60°,∠D=90°,由BC∥DE可得∠D=∠CFA=90°,所以∠BAD=∠CFA- ∠B=90°-60°=30°.故选B. 
5.(2020天津,11,3分)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应 点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是 (　　) A.AC=DE　    B.BC=EFC.∠AEF=∠D　    D.AB⊥DF
答案    D　由旋转的性质得∠ACD=∠ACB=90°,∠A=∠D,AC=DC,BC=CE,故A,B,C中结论不正确.Rt△ ABC中,∠A+∠B=90°,又∵∠A=∠D,∴∠B+∠D=90°,∴△BDF为直角三角形,∠BFD=90°,∴AB⊥DF,故 选D.
6.(2019广东广州,14,3分)一副三角板如图放置,将三角板ADE绕点A逆时针旋转α(0°