考点16 特殊的平行四边形-备战2021年中考数学考点一遍过（含答案解析）试卷

这是一份考点16 特殊的平行四边形-备战2021年中考数学考点一遍过（含答案解析）试卷，共82页。试卷主要包含了矩形的性质与判定，菱形的性质与判定，正方形的性质与判定，联系，中点四边形等内容，欢迎下载使用。

考点16 特殊的平行四边形

本单元内容是考查重点,年年都会考查,分值为15分左右,预计2021年各地中考还将出现,并且在选择、填空题中考查利用特殊四边形性质和判定求角度、长度问题的可能性比较大.解答题中考查特殊四边形的性质和判定,一般和三角形全等、解直角三角形、二次函数、动态问题综合应用的可能性比较大.对于本单元内容,要注重基础,反复练习,灵活运用.

一、矩形的性质与判定
1．矩形的性质：
1）四个角都是直角；2）对角线相等且互相平分；3）面积=长×宽=2S△ABD=4S△AOB．（如图）

2．矩形的判定：
1）定义法：有一个角是直角的平行四边形；2）有三个角是直角；3）对角线相等的平行四边形．
二、菱形的性质与判定
1．菱形的性质：
1）四边相等；2）对角线互相垂直、平分，一条对角线平分一组对角；3）面积=底×高=对角线乘积的一半．
2．菱形的判定：
1）定义法：有一组邻边相等的平行四边形；2）对角线互相垂直的平行四边形；3）四条边都相等的四边形．
三、正方形的性质与判定
1．正方形的性质：
1）四条边都相等，四个角都是直角；2）对角线相等且互相垂直平分；3）面积=边长×边长=2S△ABD=4S△AOB．
2．正方形的判定：
1）定义法：有一个角是直角，且有一组邻边相等的平行四边形；2）一组邻边相等的矩形；
3）一个角是直角的菱形；4）对角线相等且互相垂直、平分．
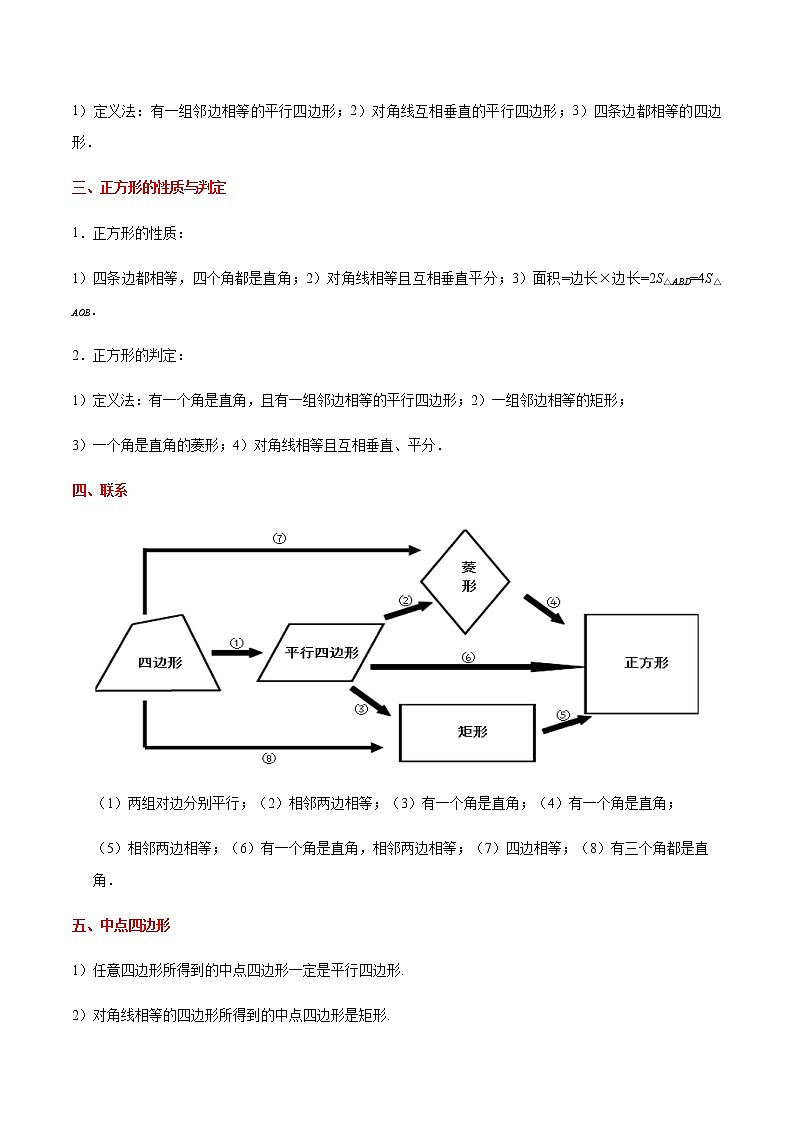
四、联系

（1）两组对边分别平行；（2）相邻两边相等；（3）有一个角是直角；（4）有一个角是直角；
（5）相邻两边相等；（6）有一个角是直角，相邻两边相等；（7）四边相等；（8）有三个角都是直角．
五、中点四边形
1）任意四边形所得到的中点四边形一定是平行四边形.
2）对角线相等的四边形所得到的中点四边形是矩形.
3）对角线互相垂直的四边形所得到的中点四边形是菱形.
4）对角线互相垂直且相等的四边形所得到的中点四边形是正方形.


考向一 矩形的性质
1．矩形除了具有平行四边形的一切性质外，还具有自己单独的性质，即：矩形的四个角都是直角；矩形的对角线相等．
2．利用矩形的性质可以推出直角三角形斜边中线的性质，即在直角三角形中，斜边上的中线等于斜边的一半．

1．（2020·广东广州市·中考真题）如图，矩形的对角线，交于点，，，过点作，交于点，过点作，垂足为，则的值为（ ）

A． B． C． D．
【答案】C
【分析】根据勾股定理求出AC=BD=10，由矩形的性质得出AO=5，证明得到OE的长，再证明可得到EF的长，从而可得到结论．
【详解】∵四边形ABCD是矩形，，
，，
，，，
，，
又，，，
，，，，同理可证，，
，，，，故选：C．
【点睛】本题主要考查了矩形的性质和相似三角形的判定与性质，熟练掌握判定与性质是解答此题的关键．
2．（2020·山东济南市·中考真题）如图，在矩形纸片ABCD中，AD＝10，AB＝8，将AB沿AE翻折，使点B落在处，AE为折痕；再将EC沿EF翻折，使点C恰好落在线段EB'上的点处，EF为折痕，连接．若CF＝3，则tan＝_____．

【答案】
【分析】连接AF，设CE＝x，用x表示AE、EF，再证明∠AEF＝90°，由勾股定理得通过AF进行等量代换列出方程便可求得x，再进一步求出B′C′，便可求得结果．
【详解】解：连接AF，设CE＝x，则C′E＝CE＝x，BE＝B′E＝10﹣x，

∵四边形ABCD是矩形，∴AB＝CD＝8，AD＝BC＝10，∠B＝∠C＝∠D＝90°，
∴AE2＝AB2+BE2＝82+（10﹣x）2＝164﹣20x+x2，EF2＝CE2+CF2＝x2+32＝x2+9，
由折叠知，∠AEB＝∠AEB′，∠CEF＝∠C′EF，
∵∠AEB+∠AEB′+∠CEF+∠C′EF＝180°，∴∠AEF＝∠AEB′+∠C′EF＝90°，
∴AF2＝AE2+EF2＝164﹣20x+x2+x2+9＝2x2﹣20x+173，
∵AF2＝AD2+DF2＝102+（8﹣3）2＝125，∴2x2﹣20x+173＝125，解得，x＝4或6，
当x＝6时，EC＝EC′＝6，BE＝B′E＝8﹣6＝2，EC′＞B′E，不合题意，应舍去，
∴CE＝C′E＝4，∴B′C′＝B′E﹣C′E＝（10﹣4）﹣4＝2，
∵∠B′＝∠B＝90°，AB′＝AB＝8，∴tan∠B'AC′＝=．故答案为：．
【点睛】本题考查了矩形的性质，折叠的性质，锐角三角函数，勾股定理，掌握折叠的性质是解题关键．

1．（2020·贵州毕节市·中考真题）如图，在矩形中，对角线，相交于点，点，分别是，的中点，连接，若，，则的长是（ ）

A． B． C． D．
【答案】D
【分析】由勾股定理求出BD的长，根据矩形的性质求出OD的长，最后根据三角形中位线定理得出EF的长即可．
【详解】∵四边形ABCD是矩形，∴∠ABC=90°，AC=BD，OA=OC=OD=OB，
∵，，∴AC= ∴BD=10cm，∴，
∵点，分别是，的中点，∴．故选：D．
【点睛】本题考查矩形的性质、三角形的中位线定理等知识，解题的关键是熟练掌握基本知识．
2．（2020·内蒙古中考真题）如图，在中，，D是的中点，，交的延长线于点E．若，，则的长为（ ）

A． B． C． D．
【答案】A
【分析】根据题意将BD,BC算出来,再利用勾股定理列出方程组解出即可．
【详解】∵AC=2,BC=,∴,
∵D是AB的中点,∴AD=CD=BD=．由题意可得:
两式相减得: ,解得DE=,BE=,故选A．
【点睛】本题考查直角三角形中点性质和勾股定理,关键在于找出等式列出方程组．

考向二 矩形的判定
1．矩形的判定：有三个角是直角的四边形是矩形；对角线相等的平行四边形是矩形．

1．（2020·湖北中考真题）已知中，下列条件：①；②；③；④平分，其中能说明是矩形的是（ ）
A．① B．② C．③ D．④
【答案】B
【分析】根据矩形的判定进行分析即可．
【详解】A. ，邻边相等的平行四边形是菱形，故A错误；
B. ，对角线相等的平行四边形是矩形，故B正确；
C. ，对角线互相垂直的平行四边形是菱形，故C错误；
D. 平分，对角线平分其每一组对角的平行四边形是菱形，故D错误．故选：B．
【点睛】本题考查了矩形的判定，熟知矩形从边，角，对角线三个方向的判定是解题的关键．
2．（2020·北京中考真题）如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．（1）求证：四边形OEFG是矩形；（2）若AD=10，EF=4，求OE和BG的长．

【答案】(1)见解析；(2)OE=5，BG=2.
【分析】(1)先证明EO是△DAB的中位线，再结合已知条件OG∥EF，得到四边形OEFG是平行四边形，再由条件EF⊥AB，得到四边形OEFG是矩形；
(2)先求出AE=5，由勾股定理进而得到AF=3，再由中位线定理得到OE=AB=AD=5，得到FG=5，最后BG=AB-AF-FG=2．
【详解】解：(1)证明:∵四边形ABCD为菱形，∴点O为BD的中点，
∵点E为AD中点，∴OE为△ABD的中位线，∴OE∥FG，
∵OG∥EF，∴四边形OEFG为平行四边形 ∵EF⊥AB，∴平行四边形OEFG为矩形．
(2)∵点E为AD的中点，AD=10，∴AE=
∵∠EFA=90°，EF=4，∴在Rt△AEF中，．
∵四边形ABCD为菱形，∴AB=AD=10，∴OE=AB=5，
∵四边形OEFG为矩形，∴FG=OE=5，∴BG=AB-AF-FG=10-3-5=2．故答案为：OE=5，BG=2．
【点睛】本题考查了矩形的性质和判定，菱形的性质、勾股定理等知识点，特殊四边形的性质和判定属于中考常考题型，需要重点掌握．

1．（2020·山东聊城·中考真题）如图，在中，，，将绕点旋转得到，使点的对应点落在上，在上取点，使，那么点到的距离等于（ ）．

A． B． C． D．
【答案】D
【分析】根据旋转的性质和30°角的直角三角形的性质可得的长，进而可得的长，过点D作DM⊥BC于点M，过点作于点E，于点F，如图，则四边形是矩形，解Rt△可得的长，即为FM的长，根据三角形的内角和易得，然后解Rt△可求出DF的长，进一步即可求出结果．
【解析】解：在中，∵，，∴AC=2AB=4，
∵将绕点旋转得到，使点的对应点落在上，
∴，∴，
过点D作DM⊥BC于点M，过点作于点E，于点F，交AC于点N，如图，则四边形是矩形，∴，
在Rt△中，，∴FM=1，
∵，∴，
在Rt△中，，∴，
即点到的距离等于．故选：D．

【点睛】本题考查了解直角三角形、矩形的判定和性质以及旋转的性质等知识，正确作出辅助线、熟练掌握解直角三角形的知识是解题的关键．
2．（2020·山东聊城·中考真题）如图，已知平行四边形ABCD中，E是BC的中点，连接AE并延长，交DC的延长线于点F，且AF＝AD，连接BF，求证：四边形ABFC是矩形．

【答案】见解析
【分析】先根据平行四边形的性质、平行线的性质得到两角一边对应相等，再根据三角形全等的判定定理与性质可得，然后根据平行四边形的判定可得四边形ABFC是平行四边形，又根据等量代换可得，最后根据矩形的判定（对角线相等的平行四边形是矩形）可得四边形ABFC是矩形．
【解析】∵四边形ABCD是平行四边形∴
∴
∵E为BC的中点∴∴∴
∵∴四边形ABFC是平行四边形
∴平行四边形ABFC是矩形．
【点睛】本题考查了平行四边形的判定与性质、三角形全等的判定定理与性质、矩形的判定等知识点，熟练运用各判定与性质是解题关键．

考向三 菱形的性质
菱形除了具有平行四边形的一切性质外，具有自己单独的性质，即：菱形的四条边都相等；
菱形的对角线互相垂直，并且每一条对角线平分一组对角．

1．（2020·江苏无锡市·中考真题）如图，在菱形中，，点在上，若，则__________．

【答案】115°
【分析】先根据菱形性质求出∠BCD，∠ACE，再根据求出∠AEC，最后根据两直线平行，同旁内角互补解题即可．
【详解】解：四边形ABCD是菱形，，∴AB∥CD，
∴∠BCD=180°-∠B=130°，∠ACE=∠BCD=65°，
∵ ，∴∠ACE=∠AEC=65°，∴∠BAE=180°-∠AEC=115°．
【点睛】本题考查了菱形性质，等腰三角形性质，解题方法较多，根据菱形性质求解∠ACE是解题关键．
2．（2020·广西中考真题）如图，在菱形ABCD中，点E，F分别是边AD，AB的中点．
（1）求证：；（2）若BE＝，∠C＝60°，求菱形ABCD的面积．

【答案】（1）详见解析；（2）2．
【分析】（1）利用菱形的性质，由SAS证明即可；
（2）证是等边三角形，得出BE⊥AD，求出AD即可．
【详解】（1）证明：∵四边形ABCD是菱形，∴AB＝AD，∵点E，F分别是边AD，AB的中点，∴AF＝AE，
在和中，，∴（SAS）；
（2）解：连接BD，如图：
∵四边形ABCD是菱形，∴AB＝AD，∠A＝∠C＝60°，∴是等边三角形，
∵点E是边AD的中点，∴BE⊥AD，∴∠ABE＝30°，
∴AE＝BE＝1，AB＝2AE＝2，∴AD＝AB＝2，
∴菱形ABCD的面积＝AD×BE＝2×＝2．

【点睛】本题考查的是菱形的性质，等边三角形的判定与性质，菱形的面积的计算，掌握以上知识是解题的关键．

1．（2020·辽宁葫芦岛市·中考真题）一张菱形纸片的边长为，高等于边长的一半，将菱形纸片沿直线折叠，使点与点重合，直线交直线于点，则的长为____________．
【答案】或
【分析】先根据题目中描述画出两种可能的图形，再结合勾股定理即可得解．
【详解】解：由题干描述可作出两种可能的图形．①MN交DC的延长线于点F，如下图所示

∵高AE等于边长的一半∴ 在Rt△ADE中，
又∵沿MN折叠后，A与B重合∴∴
②MN交DC的延长线于点F，如下图所示
同理可得，， 此时，
故答案为：或．
【点睛】本题主要考查菱形的性质、折叠的性质、勾股定理等相关知识点，根据题意作出两种图形是解题关键．
2．（2020·甘肃金昌市·中考真题）如图所示的木制活动衣帽架是由三个全等的菱形构成，根据实际需要可以调节间的距离，若间的距离调节到60，菱形的边长，则的度数是（ ）

A． B． C． D．
【答案】C
【分析】如图（见解析），先根据菱形的性质可得，再根据全等的性质可得，然后根据等边三角形的判定与性质可得，最后根据平行线的性质即可得．
【详解】如图，连接AC四边形ABCD是菱形
如图所示的木制活动衣帽架是由三个全等的菱形构成，
是等边三角形
故选：C．

【点睛】本题考查了菱形的性质、等边三角形的判定与性质、平行线的性质等知识点，理解题意，熟练掌握菱形的性质是解题关键．

考向四 菱形的判定
菱形的判定：四条边都相等的四边形是菱形；对角线互相垂直的平行四边形是菱形．

1．（2020·江苏南通市·中考真题）下列条件中，能判定▱ABCD是菱形的是（　　）
A．AC＝BD B．AB⊥BC C．AD＝BD D．AC⊥BD
【答案】D
【分析】根据菱形的判定条件即可得到结果；
【详解】解：∵四边形ABCD是平行四边形，∴当AC⊥BD时，四边形ABCD是菱形；故选：D．
【点睛】本题主要考查了菱形的判定，准确理解条件是解题的关键．
2．（2020·山东滨州市·中考真题）如图，过□ABCD对角线AC与BD的交点E作两条互相垂直的直线，分别交边AB、BC．CD、DA于点P、M、Q、N．（1）求证：PBE≌QDE；（2）顺次连接点P、M、Q、N，求证：四边形PMQN是菱形．

【答案】（1）见解析；（2）见解析
【分析】（1）由ASA证△PBE≌△QDE即可；（2）由全等三角形的性质得出EP=EQ，同理△BME≌△DNE（ASA），得出EM=EN，证出四边形PMQN是平行四边形，由对角线PQ⊥MN，即可得出结论．
【详解】（1）证明：∵四边形ABCD是平行四边形，∴EB=ED，AB∥CD，∴∠EBP=∠EDQ，
在△PBE和△QDE中，，∴△PBE≌△QDE（ASA）；
（2）证明：如图所示：

∵△PBE≌△QDE，∴EP=EQ，同理：△BME≌△DNE（ASA），∴EM=EN，
∴四边形PMQN是平行四边形，∵PQ⊥MN，∴四边形PMQN是菱形．
【点睛】本题考查了平行四边形的判定与性质，菱形的判定，全等三角形的判定与性质；熟练掌握菱形的判定和平行四边形的判定与性质，证明三角形全等是解题的关键．

1．（2020·内蒙古通辽市·中考真题）如图，是的中线，四边形是平行四边形，增加下列条件，能判断是菱形的是(　　　)

A． B． C． D．
【答案】A
【分析】根据菱形的判定方法逐一分析即可.
【详解】解：A、若，则AD=BD=CD=AE，∵四边形ADCE是平行四边形，则此时四边形ADCE为菱形，故选项正确；
B、若，则四边形ADCE是矩形，故选项错误；
C、若，则∠ADC=90°，则四边形ADCE是矩形，故选项错误；
D、若，而AB＞AD，则AE≠AD，无法判断四边形ADCE为菱形，故选项错误.故选A.
【点睛】本题考查了菱形的判定，还涉及到平行四边形的性质，矩形的判定，等腰三角形的性质，解题的关键是掌握判定定理.
2．（2020·湖南郴州市·中考真题）如图，在菱形中，将对角线分别向两端延长到点和，使得．连接．求证：四边形是菱形．

【答案】见解析
【分析】连接BD，由菱形ABCD的性质得出OA=OC，OB=OD，AC⊥BD，得出OE=OF，证出四边形BEDF是平行四边形，再由EF⊥BD，即可证出四边形BEDF是菱形．
【详解】证明：连接BD，交AC于O，如图所示：

∵四边形ABCD是菱形，∴OA=OC，OB=OD，AC⊥BD，
∵AE=CF，∴OE=OF，∴四边形BEDF是平行四边形，
∵EF⊥BD，∴四边形BEDF是菱形．
【点睛】本题考查了菱形的判定与性质，平行四边形的判定和性质，解决本题的关键是掌握菱形的判定与性质．

考向五 正方形的性质
正方形的性质=矩形的性质+菱形的性质．

1．（2020·浙江金华市·中考真题）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH.连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则的值是（ ）

A． B． C． D．
【答案】B
【分析】证明，得出．设，则，，由勾股定理得出，则可得出答案．
【详解】解：四边形为正方形，，，
，，，
又，，，
，，，．
设，为，的交点，，，
四个全等的直角三角形拼成“赵爽弦图”，，，
，．故选：．
【点睛】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，直角三角形的性质等知识，熟练掌握勾股定理的应用是解题的关键．
2．（2020·内蒙古呼和浩特市·中考真题）如图，正方形，G是边上任意一点（不与B、C重合），于点E，，且交于点F．（1）求证：；（2）四边形是否可能是平行四边形，如果可能请指出此时点G的位置，如不可能请说明理由．

【答案】（1）见解析；（2）不可能，理由见解析
【分析】（1）证明△ABF≌△DAE，从而得到AF=DE，AE=BF，可得结果；
（2）若要四边形是平行四边形，则DE=BF，则∠BAF=45°，再证明∠BAF≠45°即可.
【详解】解：（1）证明：∵正方形，∴AB=AD，∠BAF+∠DAE=90°，
∵DE⊥AG，∴∠DAE+∠ADE=90°，∴∠ADE=∠BAF，
又∵，∴∠BFA=90°=∠AED，∴△ABF≌△DAE（AAS），
∴AF=DE，AE=BF，∴；
（2）不可能，理由是：如图，若要四边形是平行四边形，
已知DE∥BF，则当DE=BF时，四边形BFDE为平行四边形，
∵DE=AF，∴BF=AF，即此时∠BAF=45°，而点G不与B和C重合，
∴∠BAF≠45°，矛盾，∴四边形不能是平行四边形.

【点睛】本题考查了全等三角形的判定和性质，正方形的性质，平行四边形的性质，解题的关键是找到三角形全等的条件.

1．（2020·广西中考真题）如图，在中，，高，正方形一边在上，点分别在上，交于点，则的长为（ ）

A． B． C． D．
【答案】B
【分析】证明△AEF∽△ABC，根据相似三角形对应边上的高线的比等于相似比即可求得．
【详解】解：∵四边形EFGH是正方形，∴EF∥BC，∴△AEF∽△ABC，∴．
设AN=x，则EF=FG=DN=60-x，∴解得：x=20所以，AN=20．故选：B．
【点睛】本题考查了正方形以及相似三角形的应用，注意数形结合的运用是解题关键．
2．（2020·山东滨州市·中考真题）如图，点P是正方形ABCD内一点，且点P到点A、B、C的距离分别为则正方形ABCD的面积为________

【答案】
【分析】如图，将△ABP绕点B顺时针旋转90°得到△CBM，连接PM，过点B作BH⊥PM于H．首先证明∠PMC=90°，推出∠CMB=∠APB=135°，推出A，P，M共线，利用勾股定理求出AB2即可．
【详解】解：如图，将△ABP绕点B顺时针旋转90°得到△CBM，连接PM，过点B作BH⊥PM于H．

∵BP=BM=，∠PBM=90°，∴PM=PB=2，
∵PC=4，PA=CM=2，∴PC2=CM2+PM2，∴∠PMC=90°，
∵∠BPM=∠BMP=45°，∴∠CMB=∠APB=135°，∴∠APB+∠BPM=180°，∴A，P，M共线，
∵BH⊥PM，∴PH=HM，∴BH=PH=HM=1，∴AH=2+1，∴AB2=AH2+BH2=（2+1）2+12=14+4，
∴正方形ABCD的面积为14+4．故答案为14+4．
【点睛】本题考查旋转的性质，全等三角形的判定和性质，正方形的性质，解直角三角形等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题．

考向六 正方形的判定
正方形的判定：以矩形和菱形的判定为基础，可以引申出更多正方形的判定方法，如对角线互相垂直平分且相等的四边形是正方形．证明四边形是正方形的一般步骤是先证出四边形是矩形或菱形，再根据相应判定方法证明四边形是正方形．


1．（2020·山东滨州市·中考真题）下列命题是假命题的是（ ）
A．对角线互相垂直且相等的平行四边形是正方形． B．对角线互相垂直的矩形是正方形．
C．对角线相等的菱形是正方形． D．对角线互相垂直平分的四边形是正方形．
【答案】D
【分析】根据正方形的各种判定方法逐项分析即可．
【详解】解：对角线互相垂直且相等的平行四边形是正方形，正确；
对角线互相垂直的矩形是正方形，正确；对角线相等的菱形是正方形，正确；
对角线互相垂直平分且相等的四边形是正方形；可知选项D是错误的．故选：D．
【点睛】本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
2．（2020·广西玉林市·中考真题）如图，四边形ABCD中，对角线AC与BD交于点O，且．（1）求证：四边形ABCD是正方形；
（2）若H是AB上的一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90度，得到线段HE，过点E分别作BC及AB的延长线的垂线，垂足分别是F，G，设四边形BGEF的面积为，以HB，BC为邻边的矩形面积为，且，当时，求AH的长；

【答案】（1）证明见解析；（2）.
【分析】（1）由题根据可得对角线相等且互相平分，可得四边形ABCD是矩形，又因为在中，利用勾股定理逆定理可得出为等腰直角三角形，可得，所以也是等腰直角三角形，可得，所以得出四边形ABCD是正方形；
（2）根据题意，易证得，可得，设，则，，可得，则，令，即：，解方程即可得出的长.
【详解】解：（1）依题意可得：，四边形为平行四边形；
又，四边形为矩形；
又在中，，且三边满足
为等腰直角三角形；,
,,,四边形为正方形；即：四边形为正方形.
（2）由题可得：,，
又，
在与中
设，则，
可得：，，令，可得，
解得：，（舍去）.即.
【点睛】本题考查正方形的判定以及与正方形相关的几何证明.在证明正方形的时候必须先证明四边形是矩形或者菱形，然后得出正方形；如果题中涉及到边之间的关系是或倍的关系，则利用勾股定理逆定理验证是否是等腰直角三角形；如果遇到直角比较多的地方，注意观察题中是否有一线三垂直，要积累和熟练应用这个全等模型.

1．（2020·四川眉山市·中考真题）下列说法正确的是（ ）
A．一组对边平行另一组对边相等的四边形是平行四边形 B．对角线互相垂直平分的四边形是菱形
C．对角线相等的四边形是矩形 D．对角线互相垂直且相等的四边形是正方形
【答案】B
【分析】利用平行四边形的判定、菱形的判定、矩形的判定及正方形的判定定理对各选项逐一判断后即可确定正确的选项．
【详解】解：A、一组对边平行，另一组对边相等的四边形是平行四边形错误，如等腰梯形；
B、对角线互相垂直平分的四边形是菱形，正确；
C、对角线相等的四边形是矩形错误，如等腰梯形；
D、对角线互相垂直且相等的四边形是正方形错误，如一般四边形对角线也可以互相垂直且相等．
故选：B．
【点睛】本题考查了命题与定理，解题的关键是了解平行四边形的判定、菱形的判定、矩形的判定及正方形的判定定理，难度一般．
2．（2020·山东威海市·中考真题）如图，在平行四边形ABCD中，对角线，，，为的中点，E为边上一点，直线交于点F，连结，．下列结论不成立的是（ ）

A．四边形为平行四边形 B．若，则四边形为矩形
C．若，则四边形为菱形 D．若，则四边形为正方形
【答案】D
【分析】根据平行四边形的性质及判定定理，以及特殊平行四边形的判定定理进行逐一判断即可得解．
【详解】A.∵四边形ABCD是平行四边形∴∴ ∵为的中点∴
在与中∴∴
又∵∴四边形为平行四边形，故A选项正确；
B.假设∵，，∴
∴∴ ∵∴
则当时， ∵四边形为平行四边形∴四边形为矩形，故B选项正确；
C.∵，∴E是AB中点∵∴
∵四边形为平行四边形∴四边形为菱形，故C选项正确；
D.当时与时矛盾，则DE不垂直于AB，则四边形不为矩形，则也不可能为正方形，故D选项错误，故选：D．
【点睛】本题主要考查了平行四边形的性质及判定定理，以及特殊平行四边形的判定定理，熟练掌握相关性质及定理的几何证明方法是解决本题的关键．

考向七 中点四边形
1．中点四边形一定是平行四边形；
2．中点四边形的面积等于原四边形面积的一半．

1．（2020·山东菏泽·中考真题）如果顺次连接四边形的各边中点得到的四边形是矩形，那么原来四边形的对角线一定满足的条件是（ ）
A．互相平分 B．相等 C．互相垂直 D．互相垂直平分
【答案】C
【分析】由于顺次连接四边形各边中点得到的四边形是平行四边形，再由矩形的判定可知，依次连接对角线互相垂直的四边形各边的中点所得四边形是矩形．
【解析】
根据题意画出图形如下：答：AC与BD 的位置关系是互相垂直．
证明：∵四边形EFGH是矩形，∴∠FEH=90°，
又∵点E、F、分别是AD、AB、各边的中点，∴EF是三角形ABD的中位线，
∴EF∥BD，∴∠FEH=∠OMH=90°，
又∵点E、H分别是AD、CD各边的中点，∴EH是三角形ACD的中位线，
∴EH∥AC，∴∠OMH=∠COB=90°，即AC⊥BD．故选C．
【点睛】此题主要考查了矩形的判定定理，画出图形进而应用平行四边形的判定以及矩形判定是解决问题的关键．
2．（2020·山东德州市·中考模拟）我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）

【答案】（1）证明见解析；（2）四边形EFGH是菱形，证明见解析；（3）四边形EFGH是正方形.
【分析】（1）如图1中，连接BD，根据三角形中位线定理只要证明EH∥FG，EH=FG即可．（2）四边形EFGH是菱形．先证明△APC≌△BPD，得到AC=BD，再证明EF=FG即可．（3）四边形EFGH是正方形，只要证明∠EHG=90°，利用△APC≌△BPD，得∠ACP=∠BDP，即可证明∠COD=∠CPD=90°，再根据平行线的性质即可证明．
【详解】（1）证明：如图1中，连接BD．
∵点E，H分别为边AB，DA的中点，∴EH∥BD，EH=BD，
∵点F，G分别为边BC，CD的中点，∴FG∥BD，FG=BD，
∴EH∥FG，EH=GF，∴中点四边形EFGH是平行四边形．
（2）四边形EFGH是菱形．
证明：如图2中，连接AC，BD．∵∠APB=∠CPD，
∴∠APB+∠APD=∠CPD+∠APD，即∠APC=∠BPD，
在△APC和△BPD中，∵AP=PB，∠APC=∠BPD，PC=PD，∴△APC≌△BPD，∴AC=BD．
∵点E，F，G分别为边AB，BC，CD的中点，∴EF=AC，FG=BD，
∵四边形EFGH是平行四边形，∴四边形EFGH是菱形．
（3）四边形EFGH是正方形．
证明：如图2中，设AC与BD交于点O．AC与PD交于点M，AC与EH交于点N．
∵△APC≌△BPD，∴∠ACP=∠BDP，∵∠DMO=∠CMP，∴∠COD=∠CPD=90°，
∵EH∥BD，AC∥HG，∴∠EHG=∠ENO=∠BOC=∠DOC=90°，
∵四边形EFGH是菱形，∴四边形EFGH是正方形．

考点：平行四边形的判定与性质；中点四边形．

1．（2020·全国九年级其他模拟）如图，四边形ABCD中，AC＝m，BD＝n，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……，如此进行下去，得到四边形A5B5C5D5的周长是（ ）

A． B． C． D．
【答案】A
【分析】根据三角形中位线定理、矩形的判定定理得到四边形A1B1C1D1是矩形，根据菱形的判定定理得到四边形A2B2C2D2是平行四边形，得到四边形A5B5C5D5为矩形，计算即可．
【详解】解：点A1，D1分别是AB、AD的中点，∴A1D1∥BD，A1D1＝BD＝n，
同理：B1C1∥BD，B1C1＝BD＝n，∴A1D1∥B1C1，A1D1＝B1C1，
∴四边形A1B1C1D1是平行四边形，∵AC⊥BD，AC∥A1B1，BD∥A1D1，∴A1B1⊥A1D1，
∴四边形A1B1C1D1是矩形，其周长为2×（m＋n）＝m＋n，
同理，四边形A2B2C2D2是平行四边形，
∵A2B2＝A1C1，B2C2＝A1C1，∴A2B2＝B2C2，∴四边形A2B2C2D2是菱形，
同理，A3B3C3D3为矩形，周长为，∴矩形A5B5C5D5的周长为，故选：A．
【点睛】本题考查的是三角形中位线定理、菱形和矩形的判定定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．
2．（2020·广东珠海市·九年级二模）顺次连接菱形四边的中点得到的四边形一定是（ ）
A．正方形 B．菱形 C．矩形 D．以上都不对
【答案】C
【分析】作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半判定出四边形EFGH是平行四边形，再根据菱形的对角线互相垂直可得EF⊥FG，然后根据有一个角是直角的平行四边形是矩形判断．
【详解】解：如图，∵四边形ABCD是菱形，∴AC⊥BD，
∵E，F，G，H是中点，∴EF∥BD，FG∥AC，∴EF⊥FG，
同理：FG⊥HG，GH⊥EH，HE⊥EF，∴四边形EFGH是矩形．故选：C．

【点睛】本题考查菱形的性质与判定定理，矩形的判定定理以及三角形的中位线定理．

考向八 特殊四边形的动态问题

1．（2020·江苏南通市·中考真题）如图①，E为矩形ABCD的边AD上一点，点P从点B出发沿折线B﹣E﹣D运动到点D停止，点Q从点B出发沿BC运动到点C停止，它们的运动速度都是1cm/s．现P，Q两点同时出发，设运动时间为x（s），△BPQ的面积为y（cm2），若y与x的对应关系如图②所示，则矩形ABCD的面积是（　　）

A．96cm2 B．84cm2 C．72cm2 D．56cm2
【答案】C
【分析】过点E作EH⊥BC，由三角形面积公式求出EH=AB=6，由图2可知当x=14时，点P与点D重合，则AD=12，可得出答案．
【详解】解：从函数的图象和运动的过程可以得出：当点P运动到点E时，x＝10，y＝30，
过点E作EH⊥BC，

由三角形面积公式得：y＝，解得EH＝AB＝6，∴BH=AE=8,
由图2可知当x＝14时，点P与点D重合，
∴ED=4,∴BC=AD＝12，∴矩形的面积为12×6＝72．故选：C．
【点睛】本题考查动点问题的函数图象，三角形的面积等知识，熟练掌握数形结合思想方法是解题的关键．
2．（2020·四川雅安市·中考真题）已知，等边三角形和正方形的边长相等，按如图所示的位置摆放（C点与E点重合），点共线，沿方向匀速运动，直到B点与F点重合．设运动时间为，运动过程中两图形重叠部分的面积为，则下面能大致反映与之间关系的函数图象是（ ）

A． B． C． D．
【答案】A
【分析】分点C在EF中点的左侧、点C在EF中点的右侧、点C在F点右侧且B在EF中点的左侧，点C在F点右侧且B在EF中点的右侧四种情况，分别求出函数的表达式即可求解．
【详解】解：设等边三角形ABC和正方形DEFG的边长都为a，运动速度为1，
当点C在EF的中点左侧时，

设AC交DE于点H，则CE=t，HE=ECtan∠ACB=t×=t，
则S=S△CEH=×CE×HE=×t×t=，可知图象为开口向上的二次函数，
当点C在EF的中点右侧时，设AB与DE 交于点M，
则EC=t，BE=a-t，ME=，∴S=，
可知图象为开口向下的二次函数；当点C在F点右侧且B在EF中点的左侧时，

S=，可知图象为开口向下的二次函数；
当点C在F点右侧且B在EF中点的右侧时，
此时BF=2a-t，MF=，∴，
可知图象为开口向上的二次函数；故选：A
【点睛】本题考查的是动点图象问题，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．

1．（2020·贵州铜仁市·中考真题）如图，在矩形ABCD中，AB＝3，BC＝4，动点P沿折线BCD从点B开始运动到点D，设点P运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是（　　）

A． B．C． D．
【答案】D
【分析】分别求出0≤x≤4、4＜x＜7时函数表达式，即可求解．
【详解】解：由题意当0≤x≤4时，y＝×AD×AB＝×3×4＝6，
当4＜x＜7时，y＝×PD×AD＝×（7﹣x）×4＝14﹣2x．故选：D．

【点睛】本题考查动点问题的函数图象，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考常考题型．
2．（2020·甘肃金昌市·中考真题）如图①，正方形中，，相交于点，是的中点，动点从点出发，沿着的路径以每秒1个单位长度的速度运动到点，在此过程中线段的长度随着运动时间的函数关系如图②所示，则的长为（ ）

A． B．4 C． D．
【答案】A
【分析】如图（见解析），先根据函数图象可知，再设正方形的边长为，从而可得，然后根据线段中点的定义可得，最后在中，利用勾股定理可求出a的值，由此即可得出答案．
【详解】如图，连接AE 由函数图象可知，
设正方形ABCD的边长为，则
四边形ABCD是正方形
，
是的中点 则在，由勾股定理得：
因此有解得则故选：A．

【点睛】本题考查了正方形的性质、勾股定理、函数图象等知识点，根据函数图象得出是解题关键．



1．（2020·山东德州市·中考真题）下列命题：
①一组对边平行，另一组对边相等的四边形是平行四边形；②对角线互相垂直且平分的四边形是菱形；
③一个角为90°且一组邻边相等的四边形是正方形；④对角线相等的平行四边形是矩形．
其中真命题的个数是（ ）
A．1 B．2 C．3 D．4
【答案】B
【分析】根据平行四边形的判定，菱形的判定，正方形的判定，矩形的判定逐一判断即可．
【详解】解：①一组对边平行，另一组对边相等的四边形是平行四边形，是假命题；
②对角线互相垂直且平分的四边形是菱形，是真命题；
③一个角为90°且一组邻边相等的四边形是正方形，是假命题；
④对角线相等的平行四边形是矩形，是真命题．故选：B．
【点睛】本题考查了平行四边形、菱形、正方形、矩形的判定，熟知特殊四边形的判定定理是解题关键．
2．（2020·江苏盐城·中考真题）如图，在菱形中，对角线相交于点为中点，．则线段的长为：（ ）

A． B． C． D．
【答案】B
【分析】因为菱形的对角线互相垂直且平分，从而有，，，又因为H为BC中点，借助直角三角形斜边上的中线等于斜边的一半即可作答．
【解析】解：∵四边形ABCD是菱形∴，，
∴△BOC是直角三角形∴∴BC=5
∵H为BC中点∴故最后答案为．
【点睛】本题考查了菱形的性质、勾股定理、直角三角形斜边上的中线等于斜边的一半，其中知道菱形的性质，对角线互相垂直且平分是解题的关键．
3．（2019·辽宁中考真题）如图，，是四边形的对角线，点，分别是，的中点，点，分别是，的中点，连接，，，，要使四边形为正方形，则需添加的条件是（ ）

A．， B．，
C．， D．，
【答案】A
【分析】证出、、、分别是、、、的中位线，得出，，，，证出四边形为平行四边形，当时，，得出平行四边形是菱形；当时，，即，即可得出菱形是正方形．
【详解】点，分别是，的中点，点，分别是，的中点，
、、、分别是、、、的中位线，
，，，，四边形为平行四边形，
当时，，平行四边形是菱形；
当时，，即，菱形是正方形；故选：．
【点睛】本题考查了正方形的判定、平行四边形的判定、菱形的判定以及三角形中位线定理；熟练掌握三角形中位线定理是解题的关键．
4．（2020·湖南株洲·中考模拟）如图，点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点，则关于四边形EFGH，下列说法正确的为（ ）

A．一定不是平行四边形 B．一定不是中心对称图形 C．可能是轴对称图形 D．当AC=BD时它是矩形
【答案】C
【解析】解：连接AC，BD，∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点，
∴EF=HG=AC，EH=FG=BD，∴四边形EFGH是平行四边形，∴四边形EFGH一定是中心对称图形，
当AC⊥BD时，∠EFG=90°，此时四边形EFGH是矩形，
当AC=BD时，EF=FG=GH=HE，此时四边形EFGH是菱形，∴四边形EFGH可能是轴对称图形，故选C．

【点睛】本题考查中点四边形；平行四边形的判定；矩形的判定；轴对称图形．
5．（2020·山东枣庄市·中考真题）如图，在矩形纸片ABCD中，AB=3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC=∠ECA，则AC的长是（　　）

A． B．6 C．4 D．5
【答案】B
【解析】∵将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，
∴AF=AB，∠AFE=∠B=90°，∴EF⊥AC，
∵∠EAC=∠ECA，∴AE=CE，∴AF=CF，∴AC=2AB=6，故选B．
【点睛】本题考查了翻折变换的性质、矩形的性质等，得到EF垂直平分AC是解题的关键．
6．（2020·浙江台州市·中考真题）下是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形．下列推理过程正确的是（ ）
A．由②推出③，由③推出① B．由①推出②，由②推出③
C．由③推出①，由①推出② D．由①推出③，由③推出②
【答案】A
【分析】根据正方形和矩形的性质定理解题即可．
【详解】根据正方形特点由②可以推理出③，再由矩形的性质根据③推出①，故选A．
【点睛】此题考查正方形和矩形的性质定理，难度一般．
7．（2020·河南中考真题）如图，在中，．边在轴上，顶点的坐标分别为和．将正方形沿轴向右平移当点落在边上时，点的坐标为（ ）

A． B． C． D．
【答案】B
【分析】先画出落在上的示意图，如图，根据锐角三角函数求解的长度，结合正方形的性质，从而可得答案．
【详解】解：由题意知：
四边形为正方形，
如图，当落在上时，
由 故选

【点睛】本题考查的是平移的性质的应用，同时考查了正方形的性质，图形与坐标，锐角三角函数，掌握以上知识是解题的关键．
8．（2020·湖北黄冈市·中考真题）若菱形的周长为16，高为2，则菱形两邻角的度数之比为（ ）
A． B． C． D．
【答案】B
【分析】如图，AH为菱形ABCD的高，AH＝2，利用菱形的性质得到AB＝4，利用正弦的定义得到∠B＝30°，则∠C＝150°，从而得到∠C：∠B的比值．
【详解】解：如图，AH为菱形ABCD的高，AH＝2，

∵菱形的周长为16，∴AB＝4，在Rt△ABH中，sinB＝＝，∴∠B＝30°，
∵AB∥CD，∴∠C＝150°，∴∠C：∠B＝5：1．故选：B．
【点睛】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了正弦的定义及应用．
9．（2020·宁夏中考真题）如图，菱形的边长为13，对角线，点E、F分别是边、的中点，连接并延长与的延长线相交于点G，则（ ）

A．13 B．10 C．12 D．5
【答案】B
【分析】连接对角线BD，交AC于点O，求证四边形BDEG是平行四边形，EG=BD，利用勾股定理求出OD的长，BD=2OD，即可求出EG．
【详解】连接BD，交AC于点O，由题意知：菱形ABCD的边长为13，点E、F分别是边CD、BC的中点，
∴AB=BC=CD=DA=13， EFBD，∵AC、BD是菱形的对角线，AC=24，∴AC⊥BD，AO=CO=12，OB=OD，
又∵ABCD，EFBD∴DEBG，BDEG在四边形BDEG中，
∵DEBG，BDEG∴四边形BDEG是平行四边形∴BD=EG
在△COD中，∵OC⊥OD，CD=13，CO=12∴OD=OB=5∴BD=EG=10故选B．

【点睛】本题主要考查了菱形的性质，平行四边形的性质及勾股定理，熟练掌握菱形、平行四边形的性质和勾股定理是解题的关键．
10．（2020·贵州遵义市·中考真题）如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（　　）

A． B． C．4 D．
【答案】D
【分析】利用菱形的面积等于两对角线之积的一半，求解菱形的面积，再利用等面积法求菱形的高即可．
【详解】解：记AC与BD的交点为，菱形,
菱形的面积
菱形的面积 故选D．

【点睛】本题考查的是菱形的性质，菱形的面积公式，勾股定理．理解菱形的对角线互相垂直平分和学会用等面积法是解题关键．
11．（2020·四川眉山市·中考真题）如图，正方形中，点是边上一点，连接，以为对角线作正方形，边与正方形的对角线相交于点，连接．以下四个结论：①；②；③；④．其中正确的个数为（ 　 ）
A．个 B．个 C．个 D．个

【答案】D
【分析】①四边形AEFG和四边形ABCD均为正方形，∠EAB、∠GAD与∠BAG的和均为90°，即可证明∠EAB与∠GAD相等；②由题意易得AD=DC，AG=FG，进而可得，∠DAG=∠CAF，然后问题可证；③由四边形AEFG和四边形ABCD均为正方形，可求证△HAF∽△FAC，则有，然后根据等量关系可求解；④由②及题意知∠ADG=∠ACF=45°，则问题可求证．
【详解】解：①∵四边形AEFG和四边形ABCD均为正方形∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG，∠GAD=90°-∠BAG∴∠EAB=∠GAD∴①正确
②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC，AG=FG∴AC=AD，AF=AG∴，即
又∵∠DAG+∠GAC=∠FAC+∠GAC∴∠DAG=∠CAF∴∴②正确
③∵四边形AEFG和四边形ABCD均为正方形，AF、AC为对角线∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF∴△HAF∽△FAC∴即
又∵AF=AE∴∴③正确
④由②知 又∵四边形ABCD为正方形， AC为对角线
∴∠ADG=∠ACF=45°∴DG在正方形另外一条对角线上∴DG⊥AC∴④正确故选：D．
【点睛】本题主要考查相似三角形的判定与性质综合运用，同时利用到正方形相关性质，解题关键在于找到需要的相似三角形进而证明．
12．（2020·辽宁沈阳市·中考真题）如图，在矩形中，，，对角线相交于点，点为边上一动点，连接，以为折痕，将折叠，点的对应点为点，线段与相交于点．若为直角三角形，则的长__________．

【答案】或1
【分析】先根据矩形的性质、折叠的性质可得，，设，从而可得，再根据直角三角形的定义分和两种情况，然后分别利用相似三角形的判定与性质、勾股定理求解即可得．
【详解】四边形ABCD是矩形，，

由折叠的性质可知，
设，则由题意，分以下两种情况：
（1）如图1，当时，为直角三角形
在和中，
，即 解得
，
在中，，即解得即

（2）如图2，当时，为直角三角形 ，
，即
在和中， ，即
解得

，即解得即综上，DP的长为或1故答案为：或1．
【点睛】本题考查了矩形的性质、折叠的性质、相似三角形的判定与性质、勾股定理等知识点，依据题意，正确画出图形，并分两种情况讨论是解题关键．
13．（2020·广西玉林市·中考真题）如图，将两张对边平行且相等的纸条交叉叠放在一起，则重合部分构成的四边形ABCD_________菱形（是，或不是）．

【答案】是
【分析】如图（见解析），先根据“两张对边平行且相等的纸条”得出，再根据平行四边形的判定可得四边形ABCD是平行四边形，然后根据三角形全等的判定定理与性质可得，最后根据菱形的判定即可得．
【详解】如图，过点B作，交DA延长线于点E，过点D作，交BA延长线于点F
由题意得：四边形ABCD是平行四边形
在和中，
平行四边形ABCD是菱形故答案为：是．

【点睛】本题考查了平行四边形与菱形的判定、三角形全等的判定定理与性质等知识点，熟练掌握平行四边形与菱形的判定是解题关键．
14．（2020·黑龙江哈尔滨市·中考真题）如图，方格纸中每个小正方形的边长为1，线段AB和线段CD的端点均在小正方形的顶点上．（1）在图中画出以AB为边的正方形，点E和点F均在小正方形的顶点上；
（2）在图中画出以CD为边的等腰三角形，点G在小正方形的顶点上，且的周长为，连接EG，请直接写出线段EG的长．

【答案】（1）画图见解析；（2）画图见解析，EG=.
【分析】（1）根据正方形的判定作图可得；（2）根据等腰三角形与勾股定理可得答案．
【详解】解：（1）如图所示，正方形ABEF即为所求；

（2）如图所示，△CDG即为所求，由勾股定理，得EG=.
【点睛】本题考查作图-应用与设计、等腰三角形的性质、勾股定理、正方形的判定和性质等知识，解题的关键是学会利用思想结合的思想解决问题，属于中考常考题型．
15．（2020·四川自贡市·中考真题）如图，在正方形中，点在边的延长线上，点在边的延长线上，且,连接和相交于点．
求证： ．

【答案】证明见解析．
【分析】利用正方形的性质证明：AB=BC=CD，∠ABE=∠BCF=90°，再证明BE=CF，可得三角形的全等，利用全等三角形的性质可得答案．
【详解】证明：∵四边形ABCD为正方形，∴AB=BC=CD，∠ABE=∠BCF=90°，
又∵CE=DF，∴CE+BC=DF+CD即BE=CF，
在△BCF和△ABE中， ∴（SAS），∴AE=BF．
【点睛】本题考查的是正方形的性质，三角形全等的判定与性质，掌握以上知识是解题的关键．
16．（2020·江苏徐州市·中考真题）我们知道：如图①，点把线段分成两部分，如果．那么称点为线段的黄金分割点．它们的比值为．

（1）在图①中，若，则的长为_____；
（2）如图②，用边长为的正方形纸片进行如下操作：对折正方形得折痕，连接，将折叠到上，点对应点，得折痕．试说明是的黄金分割点；
（3）如图③，小明进一步探究：在边长为的正方形的边上任取点，连接，作，交于点，延长、交于点．他发现当与满足某种关系时、恰好分别是、的黄金分割点．请猜想小明的发现，并说明理由．
【答案】（1）；（2）见解析；（3）当PB=BC时，、恰好分别是、的黄金分割点，理由见解析
【分析】（1）由黄金比值直接计算即可；
（2）如图，连接GE，设BG=x，则AG=20-x，易证得四边形EFCD是矩形，可求得CE，由折叠知GH=BG=x，CH=BC=20，进而EH=CE-CH，在Rt△GAE和Rt△GHE中由勾股定理得关于x的方程，解之即可证得结论；
（3）当PB=BC时，证得Rt△PBF≌Rt△CBF≌Rt△BAE,则有BF=AE，设BF=x，则AF=a-x，由AE∥PB得AE:PB=AF:BF，解得x，即可证得结论．
【详解】（1）AB=×20=（）(cm)，故答案为：；
（2）如图，连接GE，设BG=x，则GA=20-x，∵四边形ABCD是正方形，∴∠A=∠B=∠D=90º，
由折叠性质得：CH=BC=20，GE=BG=x，∠GHC=∠B=90º，AE=ED=10，
在Rt△CDE中，CE=，∴EH=，
在Rt△GHE中，
在Rt△GAE中，,
∴，解得：x=，
即，∴是的黄金分割点；

（3）当PB=BC时，、恰好分别是、的黄金分割点．
理由：∵，∴∠BCF+∠CBE=90º，又∠CBE+∠ABE=90º，∴∠ABE=∠BCF，
∵∠A=∠ABC=90º，AB=BC，∴△BAE≌△CBF（ASA），∴AE=BF，
设AE=BF=x，则AF=a-x，∵AD∥BC即AE∥PB，∴即，
∴，解得：或(舍去)，即BF=AE=，
∴，∴、分别是、的黄金分割点．
【点睛】本题考查了正方形的性质、折叠性质、勾股定理、全等三角形的判定与性质、平行线分线段成比例、解一元二次方程等知识，解答的关键是认真审题，找出相关信息的关联点，确定解题思路，进而推理、探究、发现和计算．
18．（2020·江苏宿迁市·中考真题）如图，在正方形ABCD中，点E，F在AC上，且AF=CE．求证：四边形BEDF是菱形．

【答案】见解析
【分析】由正方形的性质可得AB=AD=CD=BC，∠DAE=∠BAE=∠BCF=∠DCF=45°，由“SAS”可证△ABE≌△ADE，△BFC≌△DFC，△ABE≌△CBF，可得BE=BF=DE=DF，可得结论．
【详解】∵四边形ABCD是正方形，∴AB=AD=CD=BC，∠DAE=∠BAE=∠BCF=∠DCF=45°，
在△ABE和△ADE中，，∴△ABE≌△ADE（SAS），∴BE=DE，
同理可得△BFC≌△DFC，可得BF=DF，∵AF=CE，∴AF-EF=CE-EF，即AE=CF，
在△ABE和△CBF中，，∴△ABE≌△CBF（SAS），
∴BE=BF，∴BE=BF=DE=DF，∴四边形BEDF是菱形．
【点睛】本题考查了正方形的性质，菱形的判定，全等三角形的判定和性质，掌握正方形的性质是本题的关键．
19．（2020·湖北咸宁市·中考真题）如图，在中，以点B为圆心，长为半径画弧，交于点E，在上截取，连接．（1）求证：四边形是菱形；（2）请用无刻度的直尺在内找一点P，使（标出点P的位置，保留作图痕迹，不写作法）

【答案】（1）见解析；（2）见解析
【分析】（1）根据四边形ABCD为平行四边形，得出AF∥BE，由作图过程可知AF=BE，结合AB=BE即可证明；（2）利用菱形对角线互相垂直的性质，连接AE和BF，交点即为点P.
【详解】解：（1）根据作图过程可知：AB=BE，AF=BE，
∵四边形ABCD为平行四边形，∴AF∥BE，∵AF=BE，∴四边形ABEF为平行四边形，
∵AB=BE，∴平行四边形ABEF为菱形；
（2）如图，点P即为所作图形，

∵四边形ABEF为菱形，则BF⊥AE，∴∠APB=90°.
【点睛】本题考查了菱形的判定和性质，平行四边形的性质，解题的关键是利用相应的性质进行画图.
20．（2020·黑龙江鹤岗市·中考真题）如图，在平面直角坐标系中，矩形的边长是方程的根，连接，，并过点作，垂足为，动点从点以每秒个单位长度的速度沿方向匀速运动到点为止；点沿线段以每秒个单位长度的速度由点向点匀速运动，到点为止，点与点同时出发，设运动时间为秒

（1）线段______；（2）连接和，求的面积与运动时间的函数关系式；
（3）在整个运动过程中，当是以为腰的等腰三角形时，直接写出点的坐标．
【答案】（1）；（2）；（3）(，)或(，)
【分析】（1）解方程求出AB的长，由直角三角形的性质可求BD，BC的长，CN的长；（2）分三种情况讨论，由三角形的面积可求解；（3）分两种情况讨论，由等腰三角形的性质和勾股定理可求解．
【详解】（1）解方程得：(舍去)，∴AB=6，
∵四边形是矩形，，∴AB=CD=6，BD=2AB=12，
∴BC=AD=，∵，
∴，故答数为：；
（2）如图1，过点M作MH⊥BD于H，

∵AD∥BC，∴∠ADB=∠DBC=30°，∴MH=MD=，
∵∠DBC=30°，CN⊥BD，∴BN=， 当点P在线段BN上即时，
△PMN的面积；
当点P与点N重合即时，s=0，当点P在线段ND上即时，
△PMN的面积；
∴；
（3）如图，过点P作PE⊥BC于E，

当PN=PM=9-2t时，则DM=，MH=DM=，DH=，
∵，∴，
解得：或，即或，
则BE=或BE=，∴点P的坐标为(，)或(，)；
当PN=NM=9-2t时，∵，∴，
解得或24（不合题意舍去），∴BP=6，PE=BP=3，BE=PE=3
∴点P的坐标为(，)，综上所述：点P坐标为(，)或(，) ．
【点睛】本题是四边形综合题，考查了矩形的性质，一元二次方程的解法，三角形的面积公式，勾股定理，等腰三角形的性质，坐标与图形等知识，利用分类讨论思想解决问题是本题的关键．
21．（2020·湖北荆州市·中考真题）如图矩形ABCD中，AB=20，点E是BC上一点，将沿着AE折叠，点B刚好落在CD边上的点G处，点F在DG上，将沿着AF折叠，点D刚好落在AG上点H处，此时．（1）求证：（2）求AD的长；（3）求的值．

【答案】（1）见解析；（2）12；（3）
【分析】（1）由矩形的性质得出∠B=∠D=∠C=90°，由折叠的性质得出∠AGE=∠B=90°，∠AHF=∠D=90°，证得∠EGC=∠GFH，则可得出结论； （2）由面积关系可得出GH：AH=2：3，由折叠的性质得出AG=AB=GH+AH=20，求出GH=8，AH=12，则可得出答案； （3）由勾股定理求出DG=16，设DF=FH=x，则GF=16-x，由勾股定理得出方程，解出x=6，由锐角三角函数的定义可得出答案．
【详解】（1）证明：因为四边形ABCD是矩形 所以
，

(2)解：

(3)解：在直角三角形ADG中，
由折叠对称性知，
解得：x=6，所以：HF=6
在直角三角形GHF中，．
【点睛】本题考查了矩形的性质，翻折变换，锐角三角函数，相似三角形的判定和性质，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题．






1．（2020·四川泸州市·中考真题）下列命题是假命题的是（ ）
A．平行四边形的对角线互相平分 B．矩形的对角线互相垂直
C．菱形的对角线互相垂直平分 D．正方形的对角线互相垂直平分且相等
【答案】B
【分析】利用平行四边形、矩形、菱形、正方形的性质解题即可.
【详解】解：A、正确，平行四边形的对角线互相平分，故选项不符合；
B、错误，应该是矩形的对角线相等且互相平分，故选项符合；
C、正确，菱形的对角线互相垂直且平分，故选项不符合；
D、正确，正方形的对角线相等且互相垂直平分，故选项不符合；故选：B．
【点睛】本题考查命题与定理、特殊四边形的性质等知识，解题的关键是熟练掌握特殊四边形的性质，属于中考常考题型．
2．（2020·湖北襄阳市·中考真题）已知四边形是平行四边形，，相交于点O，下列结论错误的是（ ）
A．， B．当时，四边形是菱形
C．当时，四边形是矩形 D．当且时，四边形是正方形
【答案】B
【分析】根据平行四边形的性质，菱形，矩形，正方形的判定逐一判断即可．
【详解】解：四边形是平行四边形，，故A正确，
四边形是平行四边形，，不能推出四边形是菱形，故错误，
四边形是平行四边形，， 四边形是矩形，故C正确，
四边形是平行四边形，，， 四边形是正方形．故D正确．
故选B．
【点睛】本题考查的是平行四边形的性质，矩形，菱形，正方形的判定，掌握以上知识是解题的关键．
3．（2020·黑龙江鹤岗市·中考真题）如图，菱形的对角线、相交于点，过点作于点，连接，若，，则菱形的面积为（ ）

A．72 B．24 C．48 D．96
【答案】C
【分析】根据菱形的性质得O为BD的中点，再由直角三角形斜边上的中线等于斜边的一半，得BD的长度，最后由菱形的面积公式求得面积．
【详解】解：∵四边形是菱形，∴，，，
∵，∴，∴，
∵，∴，∵，∴，
∴菱形的面积.故选：C.
【点睛】本题主要考查了菱形的性质，直角三角形的性质，菱形的面积公式，关键是根据直角三角形的性质求得BD．
4．（2020·广西贵港市·中考真题）如图，动点在边长为2的正方形内，且，是边上的一个动点，是边的中点，则线段的最小值为（ ）

A． B． C． D．
【答案】A
【分析】作点E关于DC的对称点E，设AB的中点为点O，连接OE，交DC于点P，连接PE，由轴对称的性质及90°的圆周角所对的弦是直径，可知线段PE＋PM的最小值为OE的值减去以AB为直径的圆的半径OM，根据正方形的性质及勾股定理计算即可．
【详解】解答：解：作点E关于DC的对称点E，设AB的中点为点O，连接OE，交DC于点P，连接PE，如图：

∵动点M在边长为2的正方形ABCD内，且AM⊥BM，∴点M在以AB为直径的圆上，OM＝AB＝1，
∵正方形ABCD的边长为2，∴AD＝AB＝2，∠DAB＝90°，∵E是AD的中点，∴DE＝AD＝×2＝1，
∵点E与点E关于DC对称，∴DE＝DE＝1，PE＝PE，∴AE＝AD＋DE＝2＋1＝3，
在Rt△AOE中，OE＝＝＝，∴线段PE＋PM的最小值为：
PE＋PM＝PE＋PM＝ME＝OE−OM＝−1．故选：A．
【点睛】本题考查了轴对称−最短路线问题、圆周角定理的推论、正方形的性质及勾股定理等知识点，数形结合并熟练掌握相关性质及定理是解题的关键．
5．（2020·浙江绍兴市·中考真题）如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（　　）

A．平行四边形→正方形→平行四边形→矩形 B．平行四边形→菱形→平行四边形→矩形
C．平行四边形→正方形→菱形→矩形 D．平行四边形→菱形→正方形→矩形
【答案】B
【分析】根据对称中心的定义，根据矩形的性质，可得四边形AECF形状的变化情况．
【详解】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．
故选：B．
【点睛】考查了中心对称，矩形的性质，平行四边形的判定与性质，菱形的性质，根据EF与AC的位置关系即可求解．
6．（2020·湖北恩施土家族苗族自治州·中考真题）如图，正方形的边长为4，点在上且，为对角线上一动点，则周长的最小值为（ ）．

A．5 B．6 C．7 D．8
【答案】B
【分析】连接ED交AC于一点F，连接BF，根据正方形的对称性得到此时的周长最小，利用勾股定理求出DE即可得到答案.
【详解】连接ED交AC于一点F，连接BF，
∵四边形ABCD是正方形，∴点B与点D关于AC对称，∴BF=DF，
∴的周长=BF+EF+BE=DE+BE，此时周长最小，
∵正方形的边长为4，∴AD=AB=4，∠DAB=90°，
∵点在上且，∴AE=3，∴DE=，∴的周长=5+1=6，故选：B.

【点睛】此题考查正方形的性质：四条边都相等，四个角都是直角以及正方形的对称性质，还考查了勾股定理的计算，依据对称性得到连接DE交AC于点F是的周长有最小值的思路是解题的关键.
7．（2020·广东中考真题）如图，在正方形中，，点，分别在边，上，．若将四边形沿折叠，点恰好落在边上，则的长度为（ ）

A．1 B． C． D．2
【答案】D
【分析】由CD∥AB得到∠EFD=∠FEB=60°，由折叠得到∠FEB=∠FEB’=60°，进而得到∠AEB’=60°，然后在Rt△AEB’中由30°所对直角边等于斜边一半即可求解．
【详解】解：∵四边形ABCD是正方形，∴CD∥AB，∴∠EFD=∠FEB=60°，
由折叠前后对应角相等可知：∠FEB=∠FEB’=60°，∴∠AEB’=180°-∠FEB-∠FEB’=60°，∴∠AB’E=30°，
设AE=x,则BE=B’E=2x，∴AB=AE+BE=3x=3，∴x=1，∴BE=2x=2，故选：D．
【点睛】本题借助正方形考查了折叠问题，30°角所对直角边等于斜边的一半等知识点，折叠问题的性质包括折叠前后对应边相等，对应角相等，折叠产生角平分线，由此即可解题．
8．（2020·湖南怀化·中考真题）在矩形中，、相交于点，若的面积为2，则矩形的面积为（ ）

A．4 B．6 C．8 D．10
【答案】C
【分析】根据矩形的性质得到OA=OB=OC=OD，推出，即可求出矩形ABCD的面积.
【解析】∵四边形ABCD是矩形，对角线、相交于点，
∴AC=BD，且OA=OB=OC=OD，∴,
∴矩形的面积为,故选：C.
【点睛】此题考查矩形的性质：矩形的对角线相等，且互相平分，由此可以将矩形的；面积四等分，由此可以解决问题，熟记矩形的性质定理是解题的关键.
9．（2020·辽宁锦州市·中考真题）如图，在菱形中，P是对角线上一动点，过点P作于点E．于点F．若菱形的周长为20，面积为24，则的值为（ ）

A．4 B． C．6 D．
【答案】B
【分析】连接BP，通过菱形的周长为20，求出边长，菱形面积为24，求出SABC的面积，然后利用面积法，SABP+SCBP=SABC，即可求出的值．
【详解】解：连接BP，∵菱形ABCD的周长为20，∴AB=BC=20÷4=5，
又∵菱形ABCD的面积为24，∴SABC=24÷2=12，又SABC= SABP+SCBP∴SABP+SCBP=12，
∴ ，∵AB=BC，∴
∵AB=5，∴PE+PF=12×=．故选：B．

【点睛】本题主要考查菱形的性质，解题关键在于添加辅助线，通过面积法得出等量关系，求出PF+PE的值．
10．（2020·四川绵阳市·中考真题）如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△，当恰好经过点D时，△CD为等腰三角形，若B＝2，则A＝（　　）

A． B．2 C． D．
【答案】A
【分析】过作于，则，根据矩形的性质得，，根据旋转的性质得到，，，，推出△为等腰直角三角形，得到，设，则，，根据勾股定理即可得到结论．
【解析】解：过作于，则，

，，，四边形是矩形，，，
将绕点顺时针方向旋转后得△，
，，，，△△， ，
△为等腰三角形，△为等腰直角三角形，，
设，则，，，，
（负值舍去），，， ，，故选：．
【点睛】本题考查了旋转的性质，等腰直角三角形的性质，矩形的判定和性质，相似三角形的判定和性质，勾股定理，正确的识别图形是解题的关键．
11．（2020·黑龙江大庆市·中考真题）如图，在边长为2的正方形中，，分别为与的中点，一个三角形沿竖直方向向上平移，在运动的过程中，点恒在直线上，当点运动到线段的中点时，点，恰与，两边的中点重合．设点到的距离为，三角形与正方形的公共部分的面积为，则当时，的值为（ ）

A．或 B．或 C． D．或
【答案】A
【分析】本题应该分类讨论，从以下三个情况进行讨论，分别是：①当x<1时，重叠部分为直角三角形的面积，将其三角形面积用x表示，但是求出，与x<1相违背，要舍去；②当12时，重叠部分为一个多边形，可以从剩余部分的角度进行求解，分别将矩形PQFE、、的面积用x表示，求出x即可，将x求出后，应该与前提条件假设的x的范围进行比较，判断x的值．
【详解】解：∵在边长为2的正方形EFGH中，如图所示，当A运动到MN的中点时，点E、F恰好与AB、AC的中点重合，即AM=EM=FM=1，且MNEF，

∴AME和AMF均为等腰直角三角形，可得：ABC也是等腰直角三角形，其中AB=AC=，BC=4，
设A到EF的距离AM=x，①当x<1时，此时图形的位置如下图所示，AB与EF交于P点，AC与EF交于Q点，∵AM=x，且△APQ为等腰直角三角形，∴，解得：，但是与前提条件x<1相违背，故不存在该情况；
②当1
∵公共部分面积为，正方形剩余部分，∴，四边形ANHP是直角梯形，当AM=x，则AN=2-x，PE=x-1，HP=3-x，NH=1，
∴，解得：；
③当2＜x＜3时，此时图形的位置如下图所示，AB与EH交于K点，AB与HG交于I点，AC与FG交于L点，AC与HG交于J点，BC与EH交于P点，BC与GF交于Q点，
∵公共部分面积为，∴，
且，解得：或（舍），
④当x=3时，H,G分别是AB,AC的中点，此时重合的部分的面积为2，不符合题意；
⑤当x≥3时，重合的面积小于2，也不符合题意；所以，满足条件的AM的值为或，
故选：A．
【点睛】本题考察了移动图形间的重叠问题，需要进行分类讨论，必须要把x的移动范围进行分类，根据不同的x取值，画出不同重叠的图形，并将重叠部分的面积用x进行表示，解题的关键在于利用剩余部分的面积进行倒推求解．
12．（2020·广西中考真题）如图，在边长为的菱形中，，点分别是上的动点，且与交于点.当点从点运动到点时，则点的运动路径长为_____．

【答案】
【分析】根据题意证得，推出∠BPE =60，∠BPD =120，得到C、B、P、D四点共圆，知点的运动路径长为的长，利用弧长公式即可求解．
【详解】连接BD，

∵菱形中，，∴∠C=∠A=60，AB=BC=CD=AD，
∴△ABD和△CBD都为等边三角形，∴BD=AD，∠BDF=∠DAE=60，
∵DF=AE，∴，∴∠DBF=∠ADE，
∵∠BPE=∠BDP+∠DBF =∠BDP+∠ADE=∠BDF =60，∴∠BPD=180-∠BPE=120，
∵∠C=60，∴∠C+∠BPD =180，∴C、B、P、D四点共圆，即⊙O是的外接圆，
∴当点从点运动到点时，则点的运动路径长为的长，∴∠BOD =2∠BCD =120，
作OG⊥BD于G，根据垂径定理得：BG=GD=BD=，∠BOG =∠BOD =60，
∵，即，∴，从而点的路径长为．
【点睛】本题考查了菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，圆内接四边形的性质，弧长公式等知识，解题的关键是学会准确寻找点的运动轨迹．
13．（2020·柳州市柳林中学中考真题）如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰好落在边AD上的点F处，点G在AF上，将△ABG沿BG折叠，点A恰好落在线段BF上的H处，有下列结论：①∠EBG＝45°；②2S△BFG＝5S△FGH；③△DEF∽△ABG；④4CE＝5ED．其中正确的是_____．（填写所有正确结论的序号）

【答案】①②④
【分析】①根据折叠、矩形的性质进行推理即可；②根据等高三角形的面积比等于底边的比计算分析即可；③由矩形的性质、勾股定理及相似三角形的判定定理计算分析即可；④由矩形的性质可得CD的长，根据CE＝CD﹣ED求得CE的值，则可求得答案．
【详解】解：①由折叠的性质可知：∠CBE＝∠FBE，∠ABG＝∠FBG，
∵四边形ABCD是矩形，∴∠ABC＝90°，
∴∠EBG＝∠GBH+∠EBF＝∠CBF+∠ABF＝∠ABC＝45°．故①正确；
②由折叠的性质可知：BF＝BC＝10，BH＝AB＝6，∴HF＝BF﹣BH＝4，
∴＝＝＝，∴2S△BFG＝5S△FGH；故②正确；
③∵四边形ABCD是矩形，∴∠A＝∠D＝90°，在Rt△ABF中，AF＝＝8，
设GF＝x，即HG＝AG＝8﹣x，在Rt△HGF中，HG2+HF2＝GF2，
即（8﹣x）2+42＝x2，解得x＝5，∴AG＝3，∴FD＝2；同理可得ED＝，
∴＝＝2，＝＝，∴≠，∴△ABG与△DEF不相似，故③错误；
④∵CD＝AB＝6，ED＝，∴CE＝CD﹣ED＝，∴＝，∴4CE＝5ED．故④正确．
综上所述，正确的结论的序号为①②④，故答案为：①②④．
【点睛】本题考查了矩形的性质、折叠的性质、勾股定理及相似三角形的判定与性质等知识点，熟练掌握相关性质及定理是解题的关键．
14．（2020·辽宁营口市·中考真题）如图，在菱形ABCD中，对角线AC，BD交于点O，其中OA＝1，OB＝2，则菱形ABCD的面积为_____．

【答案】4
【分析】根据菱形的面积等于对角线之积的一半可得答案．
【详解】解：∵OA＝1，OB＝2，∴AC＝2，BD＝4，
∴菱形ABCD的面积为×2×4＝4．故答案为：4．
【点睛】本题考查菱形的性质,关键在于熟练掌握基础知识.
15．（2020·福建中考真题）设是反比例函数图象上的任意四点，现有以下结论：
①四边形可以是平行四边形；②四边形可以是菱形；③四边形不可能是矩形；④四边形不可能是正方形．其中正确的是_______．（写出所有正确结论的序号）
【答案】①④
【分析】利用反比例函数的对称性，画好图形，结合平行四边形，矩形，菱形，正方形的判定可以得到结论，特别是对②的判断可以利用反证法．
【详解】解：如图， 反比例函数的图象关于原点成中心对称，
四边形是平行四边形，故①正确，
如图，若四边形是菱形，则 显然：＜
所以四边形不可能是菱形，故②错误，

如图， 反比例函数的图象关于直线成轴对称，
当垂直于对称轴时，
四边形是矩形，故③错误，

四边形不可能是菱形，四边形不可能是正方形，故④正确，故答案为：①④．
【点睛】本题考查的是平行四边形，矩形，菱形，正方形的判定，反比例函数的对称性，掌握以上知识是解题的关键．
16．（2020·陕西中考真题）如图，在菱形ABCD中，AB＝6，∠B＝60°，点E在边AD上，且AE＝2．若直线l经过点E，将该菱形的面积平分，并与菱形的另一边交于点F，则线段EF的长为_____．

【答案】2．
【分析】过点A和点E作AG⊥BC，EH⊥BC于点G和H，可得矩形AGHE，再根据菱形ABCD中，AB＝6，∠B＝60°，可得BG＝3，AG＝3＝EH，由题意可得，FH＝FC﹣HC＝2﹣1＝1，进而根据勾股定理可得EF的长．
【详解】解：如图，过点A和点E作AG⊥BC，EH⊥BC于点G和H，得矩形AGHE，∴GH＝AE＝2，

∵在菱形ABCD中，AB＝6，∠B＝60°，∴BG＝3，AG＝3＝EH，∴HC＝BC﹣BG﹣GH＝6﹣3﹣2＝1，
∵EF平分菱形面积，∴FC＝AE＝2，∴FH＝FC﹣HC＝2﹣1＝1，
在Rt△EFH中，根据勾股定理，得EF＝＝＝2．故答案为：2．
【点睛】本题考查了菱形的性质，解决本题的关键是掌握菱形的性质．
17．（2020·福建中考真题）如图，点分别在菱形的边，上，且．求证：．

【答案】详见解析
【分析】根据菱形的性质可知AB=AD，∠B=∠D，再结合已知条件BE=DF即可证明后即可求解．
【详解】解：证明：∵四边形是菱形，∴，．
在和中，∴，∴．
【点睛】本题考查菱形的性质、全等三角形的判定与性质等基础知识，熟练掌握其性质是解决此类题的关键．
18．（2020·湖南娄底市·中考真题）如图，中，，，分别在边、上的点E与点F关于对称，连接、、、．（1）试判定四边形的形状，并说明理由；（2）求证：

【答案】（1）四边形为菱形，理由详见解析；（2）详见解析
【分析】（1）根据题意可证明，再由可得到四边形是菱形；
（2）根据直角三角形斜边上的中线的性质即可求解．
【详解】解：（1）四边形为菱形，理由如下 由可得，从而
设与相交于点O∵点E与点F关于对称∴且
在和中∴
∴，又∴四边形为菱形，

（2）∵，据（1）C ∴
又∵∴ ∴．
【点睛】此题主要考查菱形的判定与性质，解题的关键是熟知全等三角形的判定与性质、菱形的判定定理及直角三角形的性质．
19．（2020·湖南永州市·中考真题）某校开展了一次综合实践活动，参加该活动的每个学生持有两张宽为，长足够的矩形纸条．探究两张纸条叠放在一起，重叠部分的形状和面积．如图1所示，一张纸条水平放置不动，另一张纸条与它成45°的角，将该纸条从右往左平移．

（1）写出在平移过程中，重叠部分可能出现的形状．（2）当重叠部分的形状为如图2所示的四边形时，求证：四边形是菱形．（3）设平移的距离为，两张纸条重叠部分的面积为．求s与x的函数关系式，并求s的最大值．
【答案】（1）三角形，四边形（梯形、菱形），五边形；（2）见解析；（3），s的最大值为．
【分析】（1）根据平移过程中，重叠部分四边形的形状判定即可；
（2）分别过点B、D作于点E、于点F，再根据纸条的特点证明四边形ABCD是平行四边形，再证明邻边相等即可证明；（3）分、、和x=四种情况分别求出s与x的函数关系式，然后再求最大值即可．
【详解】解：（1）在平移过程中，重叠部分的形状分别为：三角形，四边形（梯形、菱形），五边形；
（2）证明：分别过点B、D作于点E、于点F，
∴∵两张纸条等宽，∴．
在和中，∴，
∵两张纸条都是矩形，，∴ ．∴四边形是平行四边形，
又∵，∴四边形是菱形；

（3）Ⅰ、如图：当时，重叠部分为三角形，如图所示，∴，∴．最大值为．

Ⅱ、如图：当时，重叠部分为梯形，如图所示，梯形的下底为，上底为，
∴，当时，s取最大值．

Ⅲ、当时，重叠部分为五边形，
．
此时．

Ⅳ、当时，重叠部分为菱形，∴．

∴∴s的最大值为．
【点睛】本题考查了平移变换、等腰直角三角形的性质、菱形的判定以及运用二次函数求最值，考查知识点较多，因此灵活运用所学知识成为解答本题的关键．
20．（2020·湖北鄂州·中考真题）如图，在平行四边形中，对角线与交于点O，点M，N分别为、的中点，延长至点E，使，连接．

（1）求证：；（2）若，且，，求四边形的面积．
【答案】(1)见解析；(2)24
【分析】(1)由四边形ABCD是平行四边形得出AB=CD，ABCD，进而得到∠BAC=∠DCA，再结合AO=CO，M,N分别是OA和OC中点即可求解；(2)证明△ABO是等腰三角形，结合M是AO的中点，得到∠BMO=∠EMO=90°，同时△DOC也是等腰三角形，N是OC中点，得到∠DNO=90°，得到EMDN，再由(1)得到EM=DN，得出四边形EMND为矩形，进而求出面积．
【解析】解：(1)证明：∵四边形ABCD是平行四边形，∴AB=CD，ABCD，OA=OC，∴∠BAC=∠DCA，
又点M，N分别为、的中点，∴，
在和中，，∴．
(2)BD=2BO，又已知BD=2AB，∴BO=AB，∴△ABO为等腰三角形；
又M为AO的中点，∴由等腰三角形的“三线合一”性质可知：BM⊥AO，
∴∠BMO=∠EMO=90°，同理可证△DOC也为等腰三角形，
又N是OC的中点，∴由等腰三角形的“三线合一”性质可知：DN⊥CO，∠DNO=90°，
∵∠EMO+∠DNO=90°+90°=180°，∴EMDN，又已知EM=BM，由(1)中知BM=DN，∴EM=DN，
∴四边形EMND为平行四边形，又∠EMO=90°，∴四边形EMND为矩形，
在Rt△ABM中，由勾股定理有：，∴AM=CN=3，
∴MN=MO+ON=AM+CN=3+3=6，∴．故答案为：．
【点睛】本题考查了平行四边形的性质、矩形的判定和性质、矩形的面积公式等，熟练掌握其性质和判定方法是解决此类题的关键．
21．（2020·四川遂宁市·）如图，在△ABC中，AB＝AC，点D、E分别是线段BC、AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：△BDE≌△FAE；（2）求证：四边形ADCF为矩形．

【答案】（1）见解析；（2）见解析
【分析】（1）首先根据平行线的性质得到∠AFE=∠DBE，再根据线段中点的定义得到AE=DE，根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到AF=BD，推出四边形ADCF是平行四边形，根据等腰三角形的性质得到∠ADC=90°，于是得到结论．
【详解】（1）证明：∵AF∥BC，∴∠AFE=∠DBE，∵E是线段AD的中点，∴AE=DE，
∵∠AEF=∠DEB，∴（AAS）；
（2）证明：∵，∴AF=BD，∵D是线段BC的中点，∴BD=CD，∴AF=CD，
∵AF∥CD，∴四边形ADCF是平行四边形，
∵AB=AC，∴，∴∠ADC=90°，∴四边形ADCF为矩形．
【点睛】本题主要考查了全等三角形的证明与矩形证明，熟练掌握相关概念是解题关键.
22．（2020·安徽中考真题）如图1．已知四边形是矩形．点在的延长线上．与相交于点，与相交于点求证：；若，求的长；
如图2，连接，求证：．

【答案】（1）见解析；（2）；（3）见解析
【分析】（1）由矩形的形及已知证得△EAF≌△DAB，则有∠E=∠ADB，进而证得∠EGB=90º即可证得结论；（2）设AE=x，利用矩形性质知AF∥BC，则有，进而得到x的方程，解之即可；
（3）在EF上截取EH=DG，进而证明△EHA≌△DGA，得到∠EAH=∠DAG，AH=AG，则证得△HAG为等腰直角三角形，即可得证结论．
【详解】（1）∵四边形ABCD是矩形，∴∠BAD=∠EAD=90º，AO=BC，AD∥BC，
在△EAF和△DAB，，∴△EAF≌△DAB(SAS)，∴∠E=∠BDA，
∵∠BDA+∠ABD=90º，∴∠E+∠ABD=90º，∴∠EGB=90º，∴BG⊥EC；
（2）设AE=x，则EB=1+x，BC=AD=AE=x，
∵AF∥BC，∠E=∠E，∴△EAF∽△EBC，∴，又AF=AB=1，
∴即，解得：，（舍去）即AE=；
（3）在EG上截取EH=DG，连接AH，
在△EAH和△DAG，，∴△EAH≌△DAG(SAS)，∴∠EAH=∠DAG，AH=AG，
∵∠EAH+∠DAH=90º，∴∠DAG+∠DAH=90º，∴∠HAG=90º，∴△GAH是等腰直角三角形，
∴即，∴GH=AG，∵GH=EG-EH=EG-DG，∴．

【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角定义、相似三角形的判定与性质、解一元二次方程等知识，涉及知识面广，解答的关键是认真审题，提取相关信息，利用截长补短等解题方法确定解题思路，进而推理、探究、发现和计算．
23．（2020·四川成都市·中考真题）在矩形的边上取一点，将沿翻折，使点恰好落在边上点处．（1）如图1，若，求的度数；（2）如图2，当，且时，求的长；（3）如图3，延长，与的角平分线交于点，交于点，当时，求出的值．

【答案】（1）15°；（2）；（3）
【分析】（1）根据矩形的性质和直角三角形的性质，先得到，再由折叠的性质可得到；
（2）由三等角证得，从而得，，再由勾股定理求出DE，则；（3）过点作于点，可证得．再根据相似三角形的性质得出对应边成比例及角平分线的性质即可得解．
【详解】（1）∵矩形，∴， 由折叠的性质可知BF=BC=2AB，，
∴，∴，∴
（2）由题意可得，，
∴∴∴，∴∴，
由勾股定理得，∴，∴；
（3）过点作于点．∴
又∵∴．∴．
∵，即∴，
又∵BM平分，，∴NG=AN，∴，
∴整理得：．

【点睛】本题是一道矩形的折叠和相似三角形的综合题，解题时要灵活运用折叠的性质和相似三角形的判定与性质的综合应用，是中考真题．