数学六年级下册1 负数教案设计

这是一份数学六年级下册1 负数教案设计，共27页。教案主要包含了单元等内容，欢迎下载使用。









第二单元：百分数（2）

















第 三 单元 圆柱和圆锥




















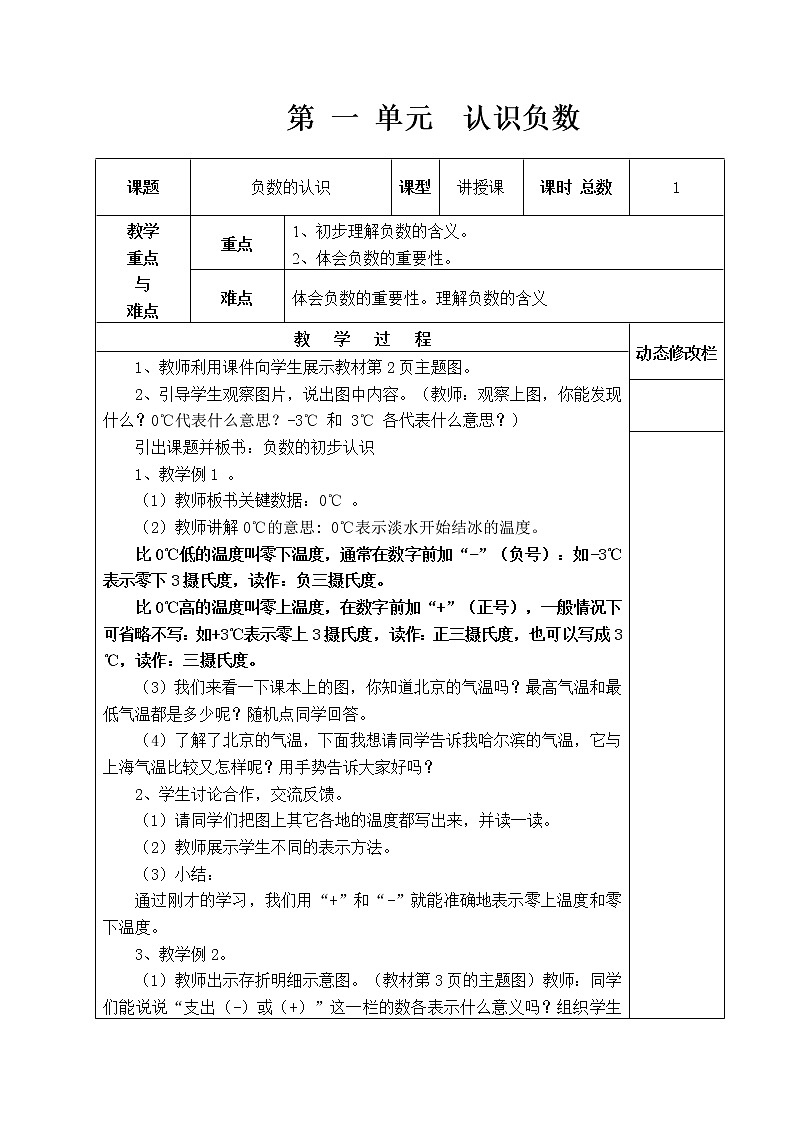
课题
负数的认识
课型
讲授课
课时 总数
1
教学


重点


与


难点
重点
1、初步理解负数的含义。


2、体会负数的重要性。
难点
体会负数的重要性。理解负数的含义
教 学 过 程
动态修改栏
1、教师利用课件向学生展示教材第2页主题图。


2、引导学生观察图片，说出图中内容。（教师：观察上图，你能发现什么？0℃代表什么意思？-3℃ 和 3℃ 各代表什么意思？）


引出课题并板书：负数的初步认识


1、教学例1 。


（1）教师板书关键数据：0℃ 。


（2）教师讲解0℃的意思: 0℃表示淡水开始结冰的温度。


比0℃低的温度叫零下温度，通常在数字前加“-”（负号）：如-3℃表示零下3摄氏度，读作：负三摄氏度。


比0℃高的温度叫零上温度，在数字前加“+”（正号），一般情况下可省略不写：如+3℃表示零上3摄氏度，读作：正三摄氏度，也可以写成3℃，读作：三摄氏度。


（3）我们来看一下课本上的图，你知道北京的气温吗？最高气温和最低气温都是多少呢？随机点同学回答。


（4）了解了北京的气温，下面我想请同学告诉我哈尔滨的气温，它与上海气温比较又怎样呢？用手势告诉大家好吗？


2、学生讨论合作，交流反馈。


（1）请同学们把图上其它各地的温度都写出来，并读一读。


（2）教师展示学生不同的表示方法。


（3）小结：


通过刚才的学习，我们用“+”和“-”就能准确地表示零上温度和零下温度。


3、教学例2。


（1）教师出示存折明细示意图。（教材第3页的主题图）教师：同学们能说说“支出（-）或（+）”这一栏的数各表示什么意义吗？组织学生分组讨论、交流，然后指名汇报。


（2）引导学生归纳总结：


像2000,500这样的数表示的是存入的钱数;而前面有“-”号的数，像-500,-132这样的数表示的是支出的钱数。


（3）教师：上述数据中500和-500意义相同吗？


（500和-500意义相反，一个是存入，一个是支出）。


你能用刚才的方法快速而又准确地表示出向东走100m和向西走200m、前进20步和后退25步吗？说说你是怎么表示的？


师把学生的表示结果一一板书在黑板上。


4、归纳正数和负数。


（1）你能把黑板上板书的这些数进行分类吗?小组讨论交流。


（2）教师展示分类的结果，适时讲解。


像+8,+4,+2000，+500,+100,+20这样的数，我们把它们叫做正数，前面的+号也可以省略不写。


像-8，-4，-500，-20这样的数，我们把它叫做负数。


（3）那么0应该归为哪一类呢？


组织学生讨论，相互发表意见。


（4）归纳：0既不是正数也不是负数，它是正数和负数的分界点。


（5）你在什么地方见过负数？


鼓励学生注意联系实际举出更多的例子。
板 书设 计
负数的认识


0℃： 淡水开始结冰的温度。


-3℃： 零下3摄氏度


3℃（+3℃）： 零上3摄氏度





正数： 负数：


+2000 -500


+500 -132


0既不是正数，也不是负数。
作业布置
1、先读一读，在把这些数填入相应的括号内。


-8 +23 17 -41 5.5 -0.7 0.004 0


正数：（ ） 负数：（ ）
课题
在直线上表示正、负数
课型
讲授课
课时 总数
1
教学


重点


与


难点
重点
借助直线初步理解正数、0、负数。
难点
充分理解正数、0、负数，能正确比较大小。
教 学 过 程
动态修改栏
师生互动（具体教、学设计）
教师用白板课件演示教材第5页的主题图。


教师：如何在一条直线上表示出他们运动后的情况呢？


1、教学例3。


（1）教师：怎样用数来表示这些学生和大树的相对位置关系呢？


组织学生在小组中议一议，然后汇报。


（2）教师结合学生的汇报，用课件出示数轴，在相应点的下方标出对应的数。





-4 -3 -2 -1 0 1 2 3 4


（3）让学生说出直线上其他几个点代表的数，让学生对数轴上的点表示的正负数形成相对完整的认识。


（4）教师总结：


我们可以在直线上表示出正数、0、负数，像这样的直线我们叫做数轴。


2、观察数轴，比较数的大小。


引导学生观察数轴。


从0起往右依次是？从0起往左依次是？你发现什么规律？


数轴以0为起点，向东为正，向西为负。0的右边是正数，左边是负数。


②在数轴上分别找到


1.5和-1.5对应的点。如果从起点分别到1.5和-1.5处，应如何运动？


师小结：


数轴除了可以表示整数，还可以表示小数、分数。每个数都能在数轴上找到它们相对应的点。
板 书设 计



在数轴上表示正数、0和负数





数轴是规定原点、正方向和单位长度的一条直线
作业布置
一、判断。


1、比0大的数都是正数。 （ 对 ）


2、比5小的数只有0、1、2、3、4。 （ 错 ）


3、0是负数。 （ 错 ）


4、气球上升2米，又上升-2米，共上升4米。 （ 错 ）


二、填空。


1、去年亩产小麦增加26千克，记作+26千克；前年亩产减少10千克，记作（-10千克）。


2、3月份出生人数300人，记作+300人； 2月份出生人数是-100人，表示（ 死亡 ）100人。


3、在数轴上表示-3的点，在原点的（ 左 ）边，离开原点（ 3 ）个单位长度。


三、填＞、＜或=。


-5（＞ ）-9 0（ ＞ ）-7 +5（＞ ）0


+1（＜ ）+14 0（ ＜ ）+1 -10（＜ ）11


-6（＜ ）+3 -2（ ＞ ）-100 -9（＜ ）+3


四、将0、+5、-3、+1、-6从小到大排列


（ -6 ＜-3 ＜ 0 ＜ +1 ＜ +5 ）



必背定义
1.在日常生活中或生产实际中，我们常用正数与负数表示具有相反意义的量。


2.前面带有“+”的数是正数，前面带有“—”的数是负数。零既不是正数也不是负数。正数前面的符号可以省略不写。


3.数轴是规定原点、正方向和单位长度的一条直线。


4.在数轴上，所有表示正数的点在原点的右边，所有表示负数的点在原点的左边。原点是表示正数和负数的点的分界点。
教学课题
百分数：折扣
教学内容
第8页“折扣”、做一做及练习二第1至3题。
教


学


目


标
知识


与


技能
明确折扣的含义，能熟练地把折扣写成分数、百分数，正确解答有关折扣的实际问题。
过程


与


方法
学会合理、灵活地选择方法，锻炼运用数学知识解决实际问题的能力。
教学重点
会解答有关折扣的实际问题。
教学难点
合理、灵活地选择方法，解答有关折扣的实际问题。
教 学 过 程
研课记录
一、情景导入


圣诞节期间各商家搞了哪些促销活动？谁来说说他们是怎样进行促销的？


二、新课讲授


1、理解“折扣”的含义。


（1）刚才大家调查到的打折是商家常用的手段，是一个商业用语，那么你所调查到的打折是什么意思呢？比如说打“七折”，你怎么理解？


（2）引导提问：如果原价是10元的铅笔盒，打七折，猜一猜现价会是多少？如果原价是1元的橡皮，打七折，现价又是多少？


（3）仔细观察，商品在打七折时，原价与现价有一个什么样的关系？


原价乘以70%恰好是标签的售价 或 现价除以原价大约都是70%。


（4）归纳定义。


通俗来讲，商店有时降价出售商品，叫做打折扣销售，通称“打折”。几折就是十分之几，也就是百分之几十。如八五折就是85%，九折就是90%。


2、解决实际问题。


例（1）爸爸给小雨买了一辆自行车，原价180元，现在商店打八五折出售。买这辆车用了多少钱？


= 1 \* GB3 ①导学生分析题意：打八五折怎么理解？是以谁为单位“1”？


= 2 \* GB3 ②先让学生找出单位“1”，然后再找出数量关系式：


原价×85%=实际售价


= 3 \* GB3 ③学生独立根据数量关系式，列式解答。


④全班交流。根据学生的汇报，板书：


例（2）爸爸买了一个随身听，原价160元，现在只花了九折的钱，比原价便宜了多少钱？


= 1 \* GB3 ①导学生理解题意：只花了九折的钱怎么理解？以谁为单位“1”？


= 2 \* GB3 ②学生试算，独立列式。


③全班交流。根据学生的汇报并板书。


3、提高运用


在某商店促销活动时，原价200元的商品打九折出售，最后剩下的个，商家再次打八折出售，最后的几商品售价多少元？


200×90%=180元 180×80%=144元


引导学生分析，学生独立完成，再集体交流，让学生明确：“折上折”相当于连续求一个数的百分之几是多少。


三、巩固练习


1、完成教材第8页“做一做”练习题。


2、完成教材第13页练习二第1~3题。
作业设计
商场在元旦期间进行打折促销活动，某品牌电视机打八折出售，杨老师在活动期间购买了一台原价3850元的电视机，比平时便宜了多少钱？








某商店打折促销，原价800元的某品牌自行车九折出售，最后剩下的几辆车，商家再次打八折出售，最后的几辆车售价多少元？








小红在某文具店买了一套文具，老板给小红打七折的优惠，小红节约了12元，这套文具原价是多少钱？



板书设计
百分数：折扣


几折就是十分之几，也就是百分之几十





（1）180×85%=153（元） （2）160-160×90%


答：买这辆车用了153元 。 =160-144


=16（元）


160×(1-90%)


= 160×10%


= 16（元）


答：比原价便宜了16钱。
教学课题
百分数：成数
教学内容
第9页“成数”、做一做及练习二第4、5题。
教


学


目


标
知识


与


技能
明确成数的含义。能熟练的把成数写成分数、百分数。正确解答有关成数的实际问题。
过程


与


方法
通过成数的计算，进一步掌握解决百分数问题的方法。
教学重点
成数的理解和计算。
教学难点
会解决生活中关于成数的实际问题。
教 学 过 程
研课记录
一、情景导入


（教材）农业收成，经常用“成数”来表示。例如，报纸上写道：“今年我省油菜籽比去年增产二成”……


同学们有留意到类似的新闻报道吗？（学生汇报相关报导）


二、新课讲授


1、理解成数的含义。


成数：表示一个数是另一个数的十分之几或百分之几十,通称“几成”


（1）刚才我们所说的成数的发展变化情况，那么这些“成数”是什么意思呢？比如说，增产“二成”，你怎么理解？（学生讨论回答，教师板书）


成数 分数 百分数


二成 十分之二 20%


(2)试说说以下成数表示什么？


①出口汽车总量比去年增加三成。


②北京出游人数比去年增加两成。


2、解决实际问题。


（1）出示教材第9页例2：


某工厂去年用电350万千瓦时，今年比去年节电二成五，今年用电多少万千瓦时？


（2）引导学生分析题目，理解题意：


①今年比去年节电二成五怎么理解？是以哪个量为单位“1”？


②找出数量关系式。


先让学生找出单位“1”，然后再找出数量关系式：


今年的用电量=去年的用电量×（1-25%）


③学生独立根据关系式，列式解答。


方法一： 350×（1-25%） 方法二：350-350×25%


=350×75% =350-350×0.25


=350×0.75 =350-87.5


=262.5(万千瓦时) =262.5（万千瓦时）


三、练习巩固


1、完成教材第9页“做一做”。


2、完成练习二第4、5题。


巩固练习：
作业设计
某乡去年的水稻产量是1500吨，今年因为受到天气灾害的影响水稻产量只有去年的八成五，今年的水稻产量是多少吨？








★梵净山2013年累计旅游人次是18万人次，2014年累计旅游人次比2013年增加一成五，2014年累计旅游人次是多少万？








★★大坪完小2013年的在校生人数有820人，比2012年在校生人数减少了二成，大坪完小2012年的在校生人数是多少？






板书设计
百分数：成数





二成 ＝ （ 十分之二 ） ＝ （ 20% ）





方法一： 350×（1-25%） 方法二：350-350×25%


=350×75% =350-350×0.25


=350×0.75 =350-87.5


=262.5(万千瓦时) =262.5（万千瓦时）



教学反思
教学课题
百分数：税率
教学内容
第10页“税率”、做一做及练习二第6、7、8、10题。
教


学


目


标
知识


与


技能
使学生知道纳税的含义和重要意义，知道应纳税额和税率的含义，以根据具体的税率计算税款。
过程


与


方法
在计算税款的过程中，加深学生对社会现象的理解，提高学生解决问题的能力。
教学重点
税率的理解和税额的计算。
教学难点
税额的计算。
教 学 过 程
研课记录
一、情景导入


1、口答算式。


（1）100的5%是多少？100×0.05=5


（2）50吨的10%是多少？50×0.1=5吨


（3）1000元的8%是多少？1000×0.08=80元


（4）50万元的20%是多少？50×0.2=10万元


2、什么是比率？比率，即比值，两数相比所得的值。


二、新课讲授


1、阅读教材第10页有关纳税的内容。说说：什么是纳税？


2、税率的认识。


（1）说明：纳税的种类很多，应纳税额的计算方法也不一样。应纳税额与各种收入的比率叫做税率，一般是由国家根据不同纳税种类定出不同的税率。


（2）试说说以下税率各表示什么意思。


A、商店按营业额的5%缴纳个人所得税。


B、某人彩票中奖后，按奖金的20%缴纳个人所得税。


3、税款计算。


（1）出示例3：一家饭店十月份的营业额约是30万元。如果按营业额的5%缴纳营业税，这家饭店十月份应缴纳营业税约多少万元？


（2）分析题目，理解题意。


引导学生理解“按营业额的5%缴纳营业税”的含义，明确这里的5%是营业税与营业额比较的结果，也就是缴纳的营业税占营业额的5%，题中“十月份的营业额是30万元”，因此十月份应缴纳的营业税就是30万元的5%。


（3）学生列出算式并计算。


相当于“求一个数的百分之几是多少”，用乘法计算。


列式：30×5% = 30×0.05 = 1.5（万元）


三、巩固练习


1、教材第10页“做一做”。


2、完成教材第14页练习二第6题 第7题 第8题 第10题。


一、计算，能简算的要简算。






作业设计
二、应用题。


★某电脑公司4月份的销售收入为800万元。按销售收入的5%缴纳增值税。纳税后该公司4月份的收入是多少万元？














★楚天餐馆8月份在缴纳了5%的营业税后，收入为5.7万元。楚天餐馆8月份的税前收入是多少?

















★★★小雨妈妈的月工资是4800元，按规定，超出3500元的部分要缴纳5%的个人所得税。小雨妈妈纳税后的月工资是多少元？



板书设计
百分数：税率





应纳税额=收入额×税率


收入额=应纳税额÷税率


税率=应纳税额÷收入额×100％





30×5％=1.5（万元）


答：10月份应缴纳营业税约1.5万元。
教学课题
百分数：利率
教学内容
第11页“利率”、做一做及练习二第9、11题。
教


学


目


标
知识


与


技能
通过教学使学生知道储蓄的意义；明确本金、利息和利率的含义；掌握计算利息的方法，会进行简单计算。
过程


与


方法
掌握计算利息的方法，会进行简单计算。
教学重点
掌握利息的计算方法。
教学难点
正确地计算利息，解决利息计算的实际问题。
教 学 过 程
研课记录
一、情景导入


随着改革开放，社会经济不断发展，人民收入增加，人们可以把暂时不用的钱存入银行，储蓄起来。一来可以支援国家建设，二来对个人也有好处，既安全、有计划，同时又得到利息，增加收入。那么，怎样计算利息呢？这就是我们今天要学的内容。


板书课题：利率


二、新课讲授


1、介绍存款的种类、形式。


存款分为活期、整存整取和零存整取等方式。


2、阅读教材第11页的内容，理解本金、利息、税后利息和利率的含义。


本金：存入银行的钱叫做本金。例题中王奶奶存入的5000元就是本金。


利息：取款时银行多支付的钱叫做利息。


利率：利息和本金的比值叫做利率。


（1）利率由银行规定，根据国家的经济发展情况，利率有时会有所调整，利率有按月计算的，也有按年计算的。


（2）阅读教材第11页表格，了解同一时期各银行的利率是一定的。


3、学会填写存款凭条。


课件出示存款凭条，请学生尝试填写。然后评讲。


（要填写的项目：户名、存期、存入金额、存种、密码、地址等，最后填上日期。）


4、利息的计算。


（1）出示利息的计算公式：


利息=本金×利率×时间


（2）计算连本带息的方法：


连本带息取回的钱 = 本金+利息


（3）学生阅读理解例4，计算后交流汇报，教师板书：


5000+5000×3.75%×2


=5000+375


=5375(元)


答：到期后可以取回5375元钱。


三、课堂小结


什么叫本金？什么叫利息？什么叫利率？如何计算利息？怎么计算取回的总钱数？


本金：存入银行的钱叫做本金。例题中王奶奶存入的5000元就是本金。


利息：取款时银行多支付的钱叫做利息。


利率：利息和本金的比值叫做利率。


利息=本金×利率×存期 取回总钱数=本金+利息



作业设计
妈妈将50000元钱存入银行，整存整取三年，年利率为4.25%。到期后将会得到多少利息？











☆王庚今年的年终奖金有3万元，他准备全部存入银行，存期为两年，年利率为3.75%。到期后，王庚一共取回多少元钱？

















☆☆☆爷爷将半年的退休金全部存入银行，存期5年，年利率是4.75%。到期后，取得利息2375元。爷爷存入的退休金是多少钱？



板书设计
百分数：利率


利息=本金×利率×存期 取回总钱数=本金+利息





5000+5000×3.75%×2


=5000+375


=5375(元)


答：到期后王奶奶可以取回5375元钱。
教学课题
百分数：整理与复习
教学内容
第12页例5、“做一做”及练习二第12至15题。
教


学


目


标
知识


与


技能
熟练地掌握百分数应用题的数量关系，并能解决问题。
过程


与


方法
通过归纳整理，是学生熟练地掌握解决百分数问题的方法。
教学重点
认真审题，用百分数解决实际问题。
教学难点
用百分数解决实际问题。
教 学 过 程
研课记录
一、复习整理


前面我们已经学习了折扣、成数、税率、利率等百分数在生活中的具体应用，今天我们一起来学习它们更多的应用，学习新知识之前，我们来回忆下之前的内容。


学生交流，汇报，教师随机板书，绘制表格。


知 识 回 顾

知识点
内 容 摘 要
解题关键

折扣
几折表示百分之几十 原价×折扣数=现价
1、找准单位“1” 2、正确理解数量关系

成数
几成表示百分之几十


税率
应缴税额=各种收入×税率


利率
利息=本金×利率×存期 取回总钱数=本金+利率


二、综合运用


课件出示例5。


1、学生读题，明确已知条件及问题，尝试说说自己的解题思路。


2、利用提问，引导学生思考回答，归纳出解题思路。


提问启发：“满100元减50元”是什么意思？


引导回答：就是在总价中取整百元部分，每个100元减去50元。不满100元的零头部分不优惠。


归纳整理解题思路：


（1）在A商场买，直接用总价乘以50%就能算出实际花费。


（2）在B商场买，先看总价中有几个100， 230里有两个100，然后从总价里减去2个50元。


3、学生独立列出算式，并计算出结果。再交流汇报，教师板书：


A商场：230×50%=115（元）


B商场：230-2×50


=230-100


=130（元）


115