人教版新课标B选修2-32.3.1离散型随机变量的数学期望教课内容ppt课件

这是一份人教版新课标B选修2-32.3.1离散型随机变量的数学期望教课内容ppt课件，共60页。PPT课件主要包含了抽象概括形成概念，注意事项，如何刻画稳定，所以X的分布列为，X服从哪种概率分布，法一公式法，法二定义法，方法小结等内容，欢迎下载使用。

10名学生在一次数学考试中的成绩如下表所示：
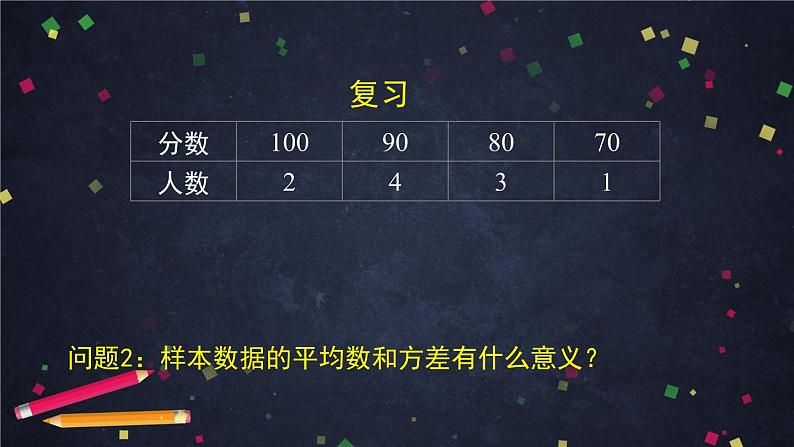
10名学生在一次数学考试中的成绩如下表所示：问题1：求这10名学生的成绩所组成样本的平均数和方差.
问题2：样本数据的平均数和方差有什么意义？
设从这10个学生中任取一个学生的成绩是离散型随机变量X，
一般地，设一个离散型随机变量X所有可能取的值是 ， ， ， ，这些值对应的概率是 ， ， ， ，则叫做这个离散型随机变量X的均值或数学期望；
一般地，设一个离散型随机变量X所有可能取的值是 ， ， ， ，这些值对应的概率是 ， ， ， ，则叫做这个离散型随机变量X的均值或数学期望； 离散型随机变量X的数学期望刻画了这个离散型随机变量的平均取值水平.
一般地，设一个离散型随机变量X所有可能取的值是 ， ， ， ，这些值对应的概率是 ， ， ， ，则叫做这个离散型随机变量X的方差；
一般地，设一个离散型随机变量X所有可能取的值是 ， ， ， ，这些值对应的概率是 ， ， ， ，则叫做这个离散型随机变量X的方差； 离散型随机变量X的方差反映了离散型随机变量取值相对于期望的平均波动大小（或说离散程度）.
问题3：随机变量的期望与它可能取值的算术平均数相同吗？
练习1. 已知离散型随机变量X的分布列如下表所示：（1）求X的可能取值的算术平均数；（2）求X的期望.
解：（1）X可能取值的算术平均数为
练习1. 已知离散型随机变量X的分布列如下表所示：（1）求X 的可能取值的算术平均数；（2）求X 的期望.
解：（1）X可能取值的算术平均数为 （2）
问题4：随机变量的期望与它可能取值的算术平均数可能相等吗？
练习2. 掷一个骰子所得的点数为X，求 .
解：X的可能取值为1，2，3，4，5，6，且因此
区分随机变量X与随机变量的期望 . 随机变量X可以取不同的值； 期望 是不变的，它由X的分布列唯一确定，反映了X取值的平均水平.
区分随机变量X与随机变量的期望 . 随机变量X可以取不同的值； 期望 是不变的，它由X的分布列唯一确定，反映了X取值的平均水平.2. 区分随机变量的期望与相应数值的算术平均数. 期望表示随机变量在概率意义下的平均值，不同于相应数值的算术平均数.
练习3. 甲、乙两名射手在同一条件下进行射击，分布列如下，判断谁的射击水平比较稳定？射手甲： 射手乙：
练习3. 甲、乙两名射手在同一条件下进行射击，分布列如下，判断谁的射击水平比较稳定？射手甲： 射手乙：解：
射手甲： 射手乙：解：
射手甲： 射手乙：解： 由 可知，甲的射击水平比较稳定.
射手甲： 射手乙：
例. 已知离散型随机变量X服从的分布列如下，且 , ,求 和 .
复习：X服从哪种概率分布？
复习：你能举出符合二点分布的随机变量的例子吗？
例. 已知某射击选手射击的命中率是0.8，那么他三次独立射击时的命中次数X的期望和方差是多少？
解：X的可能取值为0，1，2，3.
二项分布：若 ， ，则
超几何分布：若离散型随机变量X服从参数为N，M，n的超几何分布,则
例. 一个袋子里装有大小相同的4个白球和5个黑球，从中任取4个，求其中所含白球个数X的期望.
解：根据题目知所含白球数X服从N=9,M=4,n=4的超几何分布，则
解：箱子中共有9个球，X可能取值为0，1，2，3，4.
请同学们尝试概括求离散型随机变量的期望和方差的方法和步骤.
方法一：定义法找到随机变量X的所有可能取值 ；计算X取每一个值 的概率 ,得到X的分布列:计算
方法二：公式法1. 判断随机变量是否服从二点分布、二项分布、超几何分布；2. 利用公式求期望或方差.
当 时，即为二点分布
1. 设离散型随机变量X的分布列为
求 和 .