






初中数学人教版九年级下册27.2.1 相似三角形的判定一等奖课件ppt
展开利用两边和夹角判定两个三角形相似
相等的角必须是成比例的两边的夹角
对应关系不明确,勿忘分类讨论
1.探索两角分别相等的两个三角形相似的判定定理.
2.掌握利用两角来判定两个三角形相似的方法,并能进行相关计算.
3.掌握判定两个直角三角形相似的方法,并能进行相关计算.
学校举办活动,需要三个内角分别为90°,60°,30°的形状相同、大小不同的三角纸板若干. 美美手上的测量工具只有一个量角器,她该怎么做呢?
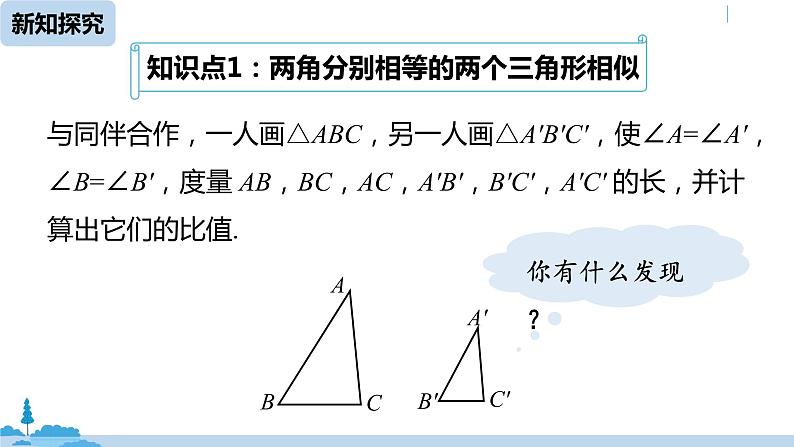
与同伴合作,一人画△ABC,另一人画△A′B′C′,使∠A=∠A′,∠B=∠B′,度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值.
证明:在 △ABC 的边 AB上,截取 AD=A′B′,过点 D 作 DE // BC,交 AC 于点 E,则有△ADE ∽△ABC,∠ADE =∠B.∵∠B=∠B′,∴∠ADE=∠B′.又∵ AD=A′B′,∠A=∠A′,∴△ADE ≌△A′B′C′,∴△A′B′C′ ∽△ABC.
如图,在△ABC与△A′B′C′ 中,∠A=∠A′,∠B=∠B′ .证明:△A′B′C′∽△ABC.
利用两组角判定两个三角形相似的定理:两角分别相等的两个三角形相似.
(1)平行线型:如图(1),若 DE//BC,则△ADE∽△ABC;(2)相交线型:如图 (2) ,若∠AED =∠B,则△AED∽△ABC;(3)子母型:如图(3),若∠ACD =∠B,则△ACD∽△ABC.
常见的相似三角形的类型
如图,在△ABC 中,∠ABC =80°,∠A = 40°,AB 的垂直平分线分别与 AC,AB 交于点 D,E,连接 BD.求证: △ABC∽△BDC.
解:∵ DE 是 AB 的垂直平分线, ∴ AD =BD, ∴ ∠ABD =∠A =40°, ∴ ∠DBC = ∠ABC -∠ABD = 40°, ∴ ∠A=∠DBC. 又∠C =∠C, ∴ △ABC ∽△BDC.
解:∵ ED⊥AB,∴∠EDA=90 ° . 又∠C=90 °,∠A=∠A, ∴ △AED ∽△ABC.
例2 如图,Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求 AD 的长.
判定直角三角形相似的方法: 有一个锐角相等的两个直角三角形相似. 两组直角边成比例的两个直角三角形相似.
∴ Rt△ABC ∽ Rt△A′B′C′.
判定直角三角形相似的方法:斜边和一条直角边成比例的两个直角三角形相似.
如图,在Rt△ABC 中,∠ACB =90°,CD⊥AB,则图中的相似三角形有( )A.0对B.1对C.2对D.3对
∠ACD =∠B,∠BCD =∠A.
△ADC∽△CDB∽△ACB.
1.如图,在等边三角形 ABC 中,点 D,E 分别在 BC,AB 上,且∠ADE =60°.求证:△ADC∽△DEB.
解:∵ △ABC 是等边三角形,∴ ∠B =∠C =60°,∴ ∠ADB =∠CAD +∠C =∠CAD+60°.∵ ∠ADE=60°,∴ ∠ADB =∠BDE +60°,∴ ∠CAD =∠BDE,∴△ADC∽△DEB.
2.如图,已知在四边形 ABCD 中,∠ADB =∠ACB,延长 AD,BC 相交于点 E.求证:(1)△ACE∽△BDE;
证明:(1)∵ ∠ACB =∠ADB, ∴ ∠ACE =∠BDE,又∠E =∠E, ∴△ACE∽△BDE.
2.如图,已知在四边形 ABCD 中,∠ADB =∠ACB,延长 AD,BC 相交于点 E.求证:(2)BE·CD =AB·DE.
将等积式转化为比例式.
观察比例式中的线段是否分别在两个形状相同的三角形中(可采用三点定形法;也可在图中标出这些线段,通过观察确定),若在两个形状相同的三角形中,可证明这两个三角形相似,若不在两个形状相同的三角形中,可利
利用相似三角形证明等积式的步骤
用如下方法转化:①等线段转化;②中间比转化;③添加辅助线构造相似三角形转化.
根据相似三角形对应边成比例或中间的转化得到比例式,再化为等积式.
3.如图,在边长为 4 的正方形 ABCD 中,P 是边 BC 上的一点 QP⊥AP 交 DC 于点 Q,设 BP =x,△ADQ 的面积为 y.(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围;
(2)点 P 在何位置时,△ADQ 的面积最小?最小面积是多少?
利用两组角判定两个三角形相似
直角三角形相似的判定方法
有一个锐角相等的两个直角三角形相似
斜边和一直角边成比例的两个直角三角形相似
两组直角边成比例的两个直角三角形相似
1.(2019·宜宾中考)如图,已知 Rt△ABC 中,CD 是斜边 AB 上的高,AC =4,BC =3,则 AD = .
3.(2019·武汉中考节选)已知 AB 是⊙O 的直径,AM 和 BN 是⊙O 的两条切线,DC 与⊙O 相切于点 E,分别交 AM,BN 于D,C 两点,如图.求证:AB2 =4AD·BC.
人教版九年级下册27.2.1 相似三角形的判定备课课件ppt: 这是一份人教版九年级下册27.2.1 相似三角形的判定备课课件ppt,共32页。PPT课件主要包含了学习目标,∴∠ADE∠B,符号语言,∠A=∠A′,ACD,ACB,ADC,勾股定理,即如果,链接中考等内容,欢迎下载使用。
人教版九年级下册27.2.1 相似三角形的判定完整版ppt课件: 这是一份人教版九年级下册27.2.1 相似三角形的判定完整版ppt课件,共19页。PPT课件主要包含了知识回顾,新课导入,问题导入,知识讲解,相似三角形判定等内容,欢迎下载使用。
人教版九年级下册27.2.1 相似三角形的判定课文配套课件ppt: 这是一份人教版九年级下册27.2.1 相似三角形的判定课文配套课件ppt,共20页。PPT课件主要包含了学习目标,温故知新,知识讲解,即学即练,随堂练习等内容,欢迎下载使用。













