





中考数学全程复习方略 第12讲 反比例函数 课件
展开考点一 反比例函数的图象和性质【主干必备】一、反比例函数解析式的三种形式1.y= ___(k≠0,k为常数). 2.y=k_________(k≠0,k为常数). 3.xy=________(k≠0,k为常数).
二、反比例函数的图象与性质1.反比例函数y= (k为常数,k≠0)的图象是______________,且关于___________对称. 2.反比例函数y= (k为常数,k≠0)的图象和性质
【微点警示】双曲线不是连续曲线,而是两支在不同象限的曲线,所以比较函数值大小时,要注意所判断的点是否在同一象限,再结合每个象限内反比例函数图象的增减性来比较.
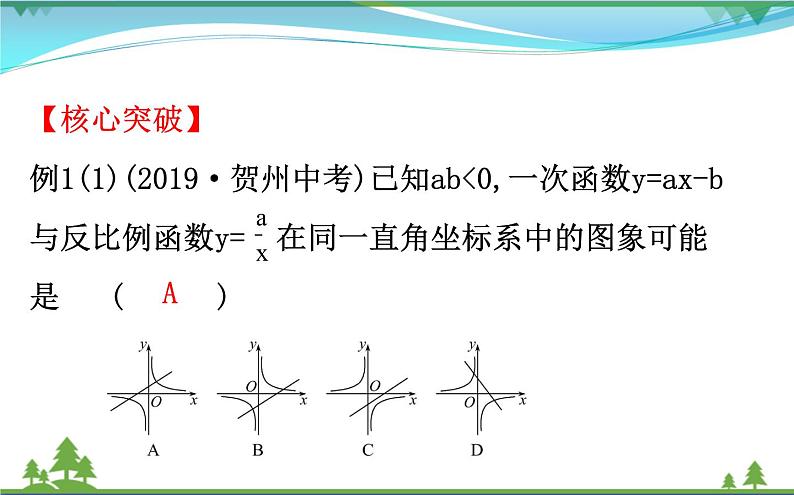
【核心突破】例1(1)(2019·贺州中考)已知ab<0,一次函数y=ax-b与反比例函数y= 在同一直角坐标系中的图象可能是( )
(2)(2019·天津中考)若点A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数y=- 的图象上,则y1,y2,y3的大小关系是( )A.y2
(2)先假设字母系数的取值,确定不同函数的图象的位置,再看在同一直角坐标系内不同函数的图象与之是否对应.
【题组过关】1.(2019·海南中考)如果反比例函数y= (a是常数)的图象在第一、三象限,那么a的取值范围是( )A.a<0B.a>0C.a<2D.a>2
2.(2019·天津南开区期末)若点(x1,y1),(x2,y2)都是反比例函数y=- 图象上的点,并且y1<0
4.(2019·娄底双峰期末)在反比例函数y= 图象的每一条曲线上,y都随x的增大而减小,则m的取值范围是__________.
考点二 求反比例函数的解析式【核心突破】例2(2019·广东中考)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A,B两点,其中点A的坐标为(-1,4),点B的坐标为(4,n).
(1)根据图象,直接写出满足kx+b> 的x的取值范围.(2)求这两个函数的表达式.(3)点P在线段AB上,且S△AOP∶S△BOP=1∶2,求点P的坐标.
【思路点拨】(1)根据一次函数图象在反比例图象的上方,可求x的取值范围.(2)将点A,点B坐标代入两个表达式可求k2,n,k,b的值,从而求得表达式.(3)根据三角形面积的比例,可得答案.
【自主解答】(1)∵点A的坐标为(-1,4),点B的坐标为(4,n).由图象可得:kx+b> 的x的取值范围是x<-1或0
【明·技法】确定反比例函数的解析式的方法
【题组过关】1.(2019·安徽模拟)已知:如图,直线l经过点A(-2,0)和点B(0,1),点M在x轴上,过点M作x轴的垂线交直线l于点C,若OM=2OA,则经过点C的反比例函数表达式为____________.世纪金榜导学号
2.(2019·盐城中考)如图,一次函数y=x+1的图象交y轴于点A,与反比例函数y= (x>0)的图象交于点B(m,2).(1)求反比例函数的表达式.(2)求△AOB的面积.
【解析】(1)∵点B(m,2)在直线y=x+1上,∴2=m+1,得m=1,∴点B的坐标为(1,2),∵点B(1,2)在反比例函数y= (x>0)的图象上,∴2= ,得k=2,即反比例函数的表达式为y= .
(2)将x=0代入y=x+1,得y=1,则点A的坐标为(0,1),∵点B的坐标为(1,2),∴△AOB的面积是
考点三 一次函数与反比例函数的综合【核心突破】例3如图,一次函数y=kx+b与反比例函数y= 的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M,N两点.
(1)求一次函数的解析式.(2)根据图象直接写出kx+b- >0中x的取值范围.(3)求△AOB的面积.
【明·技法】根据一次函数和反比例函数的图象写不等式的解集的步骤(1)数形结合:根据题意画出图象.(2)找交点:根据函数图象,找到两函数的交点坐标.
(3)画三线:根据两条函数的交点画出三条垂直于x轴的直线.(4)分四域:以三线为界可将直角平面划分为四个区域.(5)定大小:根据“上大下小”原则.
如果一次函数图象与反比例函数图象有交点时,就可以利用上面的步骤去解决问题;若没有交点时,可以借助y轴分两个区域,再直接用“上大下小”原则去解决问题.
【题组过关】1.(2019·衡阳中考)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= (m为常数且m≠0)的图象都经过A(-1,2),B(2,-1),结合图象,则不等式kx+b> 的解集是( )
A.x<-1B.-1
2.(2019·长沙中考)如图,函数y= (k为常数,k>0)的图象与过原点O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.连接OM.现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为
1,△OAM为等边三角形,则k=2+ ;④若MF= MB,则MD=2MA.其中正确的结论的序号是_____________.
3.(2019·聊城中考)如图,点A ,B(3,m)是直线AB与反比例函数y= (x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.世纪金榜导学号
(1)求直线AB的表达式.(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
【解析】(1)∵点A ,B(3,m)在反比例函数y= (x>0)图象上,∴4= ,∴n=6,∴反比例函数的表达式为y= (x>0),将点B(3,m)代入y= (x>0)得m=2,∴B(3,2),设直线AB的表达式为y=kx+b(k≠0),
∴ ∴直线AB的表达式为y=- x+6.
(2)由点A,B坐标得AC=4,点B到AC的距离为 ∴S1= 设AB与y轴的交点为E,可得E(0,6),如图:
∴DE=6-1=5,由点A ,B(3,2)知点A,B到DE的距离分别为 ,3,∴S2=S△BDE-S△ADE= ∴S2-S1=
考点四 反比例函数的实际应用【核心突破】例4(2018·河北中考)如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y= (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落
路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5, M,A的水平距离是vt米.
(1)求k,并用t表示h.(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离.
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
【自主解答】(1)由题意,将点A(1,18)代入y= ,得:18= ,∴k=18.设h=at2,把t=1,h=5代入,∴a=5,∴h=5t2.
(2)∵v=5,AB=1,∴x=5t+1,∵h=5t2,OB=18,∴y=-5t2+18.由x=5t+1,则t= (x-1),∴y=- (x-1)2+18=- x2+ x+ ,当y=13时,13=- (x-1)2+18,解得x=6或-4,∵x≥1,∴x=6,
把x=6代入y= ,得y=3.∴运动员与正下方滑道的竖直距离是13-3=10(米).(3)略
【明·技法】本题是二次函数和反比例函数所构成的分段函数,并进一步利用反比例函数解决实际问题,解决这类问题的关键是审清题目,理清步骤:先根据点的坐标确定解析式,再根据方程或不等式解决实际问题.
【题组过关】1.(2019·安徽模拟)一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器体积时,气体的密度也随之改变.密度ρ(单位:kg/m3)与体积V(单位:m3)满足函数关系式ρ= (k为常数,k≠0),其图象如图所示,那么当V≥6 m3时,气体的密度ρ(单位:kg/m3)的取值范围是( )
A.ρ≤1.5 B.0<ρ≤1.5C.ρ≥1.5D.ρ>1.5
2.(2019·杭州中考)方方驾驶小汽车匀速从A地行驶到B地,行驶路程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.(1)求v关于t的函数表达式.
(2)方方上午8点驾驶小汽车从A地出发.①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.②方方能否在当天11点30分前到达B地?说明理由.
【解析】(1)∵vt=480,且全程速度限定为不超过120千米/小时,∴v关于t的函数表达式为v= (t≥4).(2)①上午8点至12点48分时间长为 小时,8点至14点时间长为6小时.将t=6代入v= 得v=80;将t= 代入v= 得v=100.∴小汽车行驶速度v的范围为80≤v≤100.
②方方不能在当天11点30分前到达B地.理由如下:上午8点至11点30分时间长为 小时,将t= 代入v= 得v= >120,故方方不能在当天11点30分前到达B地.
3.(2019·兰州永登期末)为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题:世纪金榜导学号
(1)药物燃烧时,y关于x的函数关系式为____________,自变量x的取值范围为____________;药物燃烧后,y关于x的函数关系式为____________. (2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过____________分钟后,员工才能回到办公室.
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
中考数学全程复习方略 第25讲 圆的认识 课件: 这是一份中考数学全程复习方略 第25讲 圆的认识 课件,共59页。PPT课件主要包含了轴对称图形,径所在直线,平分弦,两条弧,垂直于弦,1或7,自主解答略等内容,欢迎下载使用。
中考数学全程复习方略 第10讲 函数初步 课件: 这是一份中考数学全程复习方略 第10讲 函数初步 课件,共60页。PPT课件主要包含了有序实数对,互为相反数,x-y,-xy,-x-y,唯一确定,x≥2且x≠3,横坐标,纵坐标等内容,欢迎下载使用。
中考数学全程复习方略 第4讲 分式 课件: 这是一份中考数学全程复习方略 第4讲 分式 课件,共60页。PPT课件主要包含了公因式,基本性质,同分母,自主解答,解析原式等内容,欢迎下载使用。












