






中考数学全程复习方略 第13讲 二次函数的图象与性质 课件
展开考点一 二次函数的图象和性质【主干必备】一、二次函数的概念及其关系式1.二次函数的概念:形如________________(a,b,c是常数,a≠0)的函数.
2.二次函数的解析式:(1)一般式:______________________. (2)顶点式:y=a(x-h)2+k(a≠0),其顶点坐标是____________.
y=ax2+bx+c(a≠0)
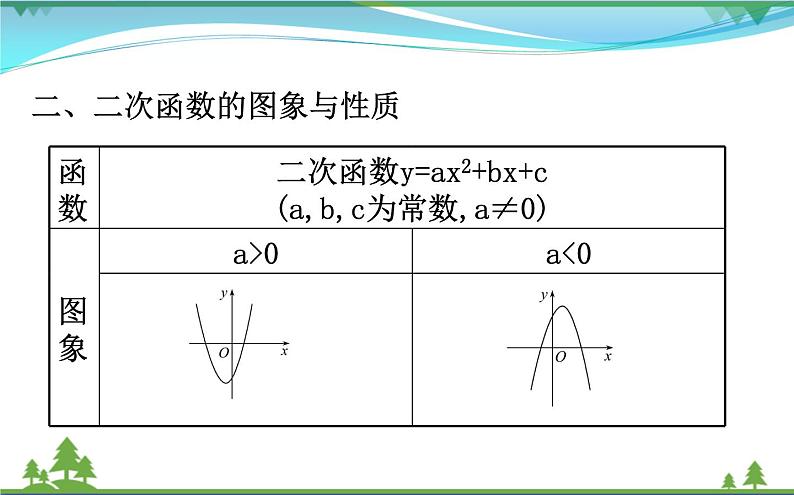
二、二次函数的图象与性质
【核心突破】例1(2018·成都中考)关于二次函数y=2x2+4x-1,下列说法正确的是( )A.图象与y轴的交点坐标为(0,1)B.图象的对称轴在y轴的右侧C.当x<0时,y的值随x值的增大而减小D.y的最小值为-3
【明·技法】由二次函数解析式判断性质的方法1.由函数顶点式直接确定顶点坐标和对称轴.2.根据开口方向和顶点坐标确定函数的增减性或函数的最值.3.根据b2-4ac的符号确定其与x轴的交点个数.
【题组过关】1.(2019·自贡中考)一次函数y=ax+b与反比例函数y= 的图象如图所示,则二次函数y=ax2+bx+c的大致图象是( )
2.(2019·兰州中考)已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是( )A.2>y1>y2 B.2>y2>y1C.y1>y2>2D.y2>y1>2
3.(2019·安庆桐城市期末)二次函数y=-x2+(8-m)x+12,当x>2时,y随着x的增大而减小;当x<2时,y随着x的增大而增大,则m的值为( )A.-4 B.4 C.6 D.10
4.(2019·上海静安区一模)抛物线y=ax2+(a-1)(a≠0)经过原点,那么该抛物线在对称轴左侧的部分是____________的.(填“上升”或“下降”)
考点二 二次函数图象的平移【核心突破】例2(1)(2019·济宁中考)将抛物线y=x2-6x+5向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A.y=(x-4)2-6 B.y=(x-1)2-3C.y=(x-2)2-2D.y=(x-4)2-2
(2)(2018·绍兴中考)若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A.(-3,-6)B.(-3,0)C.(-3,-5)D.(-3,-1)
【明·技法】二次函数图象的平移变换(1)具体步骤:先利用配方法把二次函数化成y=a(x-h)2+k的形式,确定其顶点(h,k),然后作出二次函数y=ax2的图象,将抛物线y=ax2平移,使其顶点平移到(h,k).具体平移方法如图所示:
(2)平移规律:在原有函数的基础上“左加右减”.
【题组过关】1.(2019·绍兴中考)在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线y=(x+3)(x-5),则这个变换可以是( )A.向左平移2个单位 B.向右平移2个单位C.向左平移8个单位D.向右平移8个单位
2.(2019·台州温岭市期末)把抛物线y=ax2+bx+c的图象先向左平移2个单位长度,再向下平移3个单位长度,所得的图象的解析式是y=x2+5x+5,则a-b+c的值为 ( )A.2 B.4C.8 D.14
3.(2019·广东模拟)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为________.
4.(2019·安徽模拟)如图,抛物线y1=ax2-x+c与x轴交于点A(-3,0)和点B,并经过点 ,抛物线y1的顶点为C.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
(1)求抛物线y2的表达式.(2)在直线l上是否存在点P,使△PBC为等腰三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
【解析】(1)由于抛物线y1=ax2-x+c与x轴交于点A(-3,0)和点B,并经过点 ,∴ 解得 ∴抛物线y1= 当y1=0时, =0,解得x1=-3,x2=1,
∴B点的坐标为(1,0),∵将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.∴抛物线y2的表达式为:y2=- (x-1)2.
(2)在直线l上存在点P,使△PBC是等腰三角形,由y1=- x2-x+ =- (x+1)2+2可知C点的坐标为(-1,2),根据勾股定理得BC= 设P点的坐标为(1,m),
分三种情况:①当PB=PC时,m2=22+(m-2)2,解得m=2,此时点P坐标为(1,2);②当PB=BC时,m2=(2 )2,解得m=±2 ,此时点P坐标为(1,2 )或(1,-2 );
③当PC=BC时,22+(m-2)2=(2 )2,解得m=4或m=0(舍去),此时点P坐标为(1,4);综上,△PBC是等腰三角形时,点P的坐标为(1,2)或(1,2 )或(1,-2 )或(1,4).
考点三 二次函数图象与系数的关系【核心突破】例3(2019·随州中考)如图所示,已知二次函数y=ax2+ bx+c的图象与x轴交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,则下列结论:①abc<0;②a+
=0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的有( )A.1个 B.2个 C.3个 D.4个
【明·技法】二次函数y=ax2+bx+c的图象与字母系数的关系
【题组过关】1.(2019·凉山州中考)二次函数y=ax2+bx+c的部分图象如图所示,有以下结论:①3a-b=0;②b2-4ac>0;③5a-2b+c>0;④4b+3c>0,其中错误结论的个数是( )A.1 B.2 C.3 D.4
2.(2019·汕头潮南区期末)如图,抛物线y=ax2+bx+c (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
①4ac
如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )A.10 m B.15 m C.20 m D.22.5 m
(2)(2018·湖州中考)已知抛物线y=ax2+bx-3(a≠0)经过点(-1,0),(3,0),求a,b的值.
【自主解答】∵抛物线y=ax2+bx-3(a≠0)经过点(-1,0), (3,0),∴ 解得 即a的值是1,b的值是-2.
【明·技法】确定二次函数的解析式
易错警示:(1)用顶点式代入顶点坐标时横坐标容易弄错符号.(2)所求的二次函数解析式最后要化成一般式.
【题组过关】1.(2019·杭州下城区期末)已知二次函数y=ax2+4x+c,当x=-2时,函数值是-1;当x=1时,函数值是5,则此二次函数的解析式为( )A.y=2x2+4x-1B.y=x2+4x-2C.y=-2x2+4x+1D.y=2x2+4x+1
2.(2019·沧州青县期末)二次函数的部分图象如图所示,对称轴是x=-1,则这个二次函数的解析式为世纪金榜导学号( )A.y=-x2+2x+3B.y=x2+2x+3C.y=-x2+2x-3D.y=-x2-2x+3
3.抛物线y=ax2+bx+c经过A(-2,4),B(6,4)两点,且顶点在x轴上,则该抛物线解析式为______________.
考点五 二次函数与方程、不等式的关系【核心突破】例5(1)(2019·济宁中考)如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是_________________.
(2)(2018·云南中考)已知二次函数y=- x2+bx+c的图象经过A(0,3),B(-4,- )两点.①求b,c的值.②二次函数y=- x2+bx+c的图象与x轴是否有公共点,若有,求公共点的坐标;若没有,请说明情况.
【自主解答】①把A(0,3),B(-4,- )分别代入y=- x2+bx+c,得 解得
②由①可得,该抛物线解析式为: Δ= >0,所以二次函数y=- x2+ bx+c的图象与x轴有公共点.∵- x2+ x+3=0的解为:x1=-2,x2=8.∴公共点的坐标是(-2,0)或(8,0).
【明·技法】二次函数与一元二次方程以及不等式之间的关系(1)二次函数与一元二次方程的关系①二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,则两个交点的横坐标是相应的一元二次方程ax2+bx +c=0(a≠0)的两个解.
②二次函数的图象与x轴交点的个数由相应的一元二次方程的根的判别式的符号确定.
(2)利用二次函数图象解不等式的方法不等式ax2+bx+c>0(或ax2+bx+c< 0 )的解集就是二次函数y=ax2+bx+c的图象在 x 轴上(下)方的点所对应的 x的取值范围,不等式如果带有等号,其解集也相应带有等号.a>0时, y>0取两边,y<0取中间.
【题组过关】1.(2019·深圳罗湖区期末)二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )A.x1=-1,x2=5 B.x1=-2,x2=4C.x1=-1,x2=2D.x1=-5,x2=5
2.(2019·潍坊中考)抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-1
4.(2019·济南长清区期末)如图,二次函数y=ax2+bx+c的图象与x轴交于(3,0),对称轴是直线x=1,当函数值y>0时,自变量x的取值范围是_____________.
中考数学全程复习方略 第25讲 圆的认识 课件: 这是一份中考数学全程复习方略 第25讲 圆的认识 课件,共59页。PPT课件主要包含了轴对称图形,径所在直线,平分弦,两条弧,垂直于弦,1或7,自主解答略等内容,欢迎下载使用。
中考数学全程复习方略 第10讲 函数初步 课件: 这是一份中考数学全程复习方略 第10讲 函数初步 课件,共60页。PPT课件主要包含了有序实数对,互为相反数,x-y,-xy,-x-y,唯一确定,x≥2且x≠3,横坐标,纵坐标等内容,欢迎下载使用。
中考数学全程复习方略 第4讲 分式 课件: 这是一份中考数学全程复习方略 第4讲 分式 课件,共60页。PPT课件主要包含了公因式,基本性质,同分母,自主解答,解析原式等内容,欢迎下载使用。












