中考数学全程复习方略 第25讲 圆的认识 课件

这是一份中考数学全程复习方略 第25讲 圆的认识 课件，共59页。PPT课件主要包含了轴对称图形，径所在直线，平分弦，两条弧，垂直于弦，1或7，自主解答略等内容，欢迎下载使用。

考点一　垂径定理及推论【主干必备】一、圆的定义及圆的轴对称性1.定义:在一个平面内,线段OA绕它固定的一个端点O旋转___________,另一个端点A所形成的图形. 
2.轴对称性:圆是_________________,任何一条___________________都是它的对称轴. 
二、垂径定理及推论1.垂径定理:垂直于弦的直径_____________,并且平分弦所对的_____________. 2.推论:平分弦(不是直径)的直径_______________,并且平分弦所对的_____________. 
【微点警示】(1)注意“知二推三”:一条直线满足:①过圆心,②垂直于弦,③平分弦,④平分弦所对优弧,⑤平分弦所对劣弧,这五个结论中的两个,可以推得其他三个结论成立.(2)注意“非直径”条件:若一条直径所平分的弦也是直径,则推论不成立.
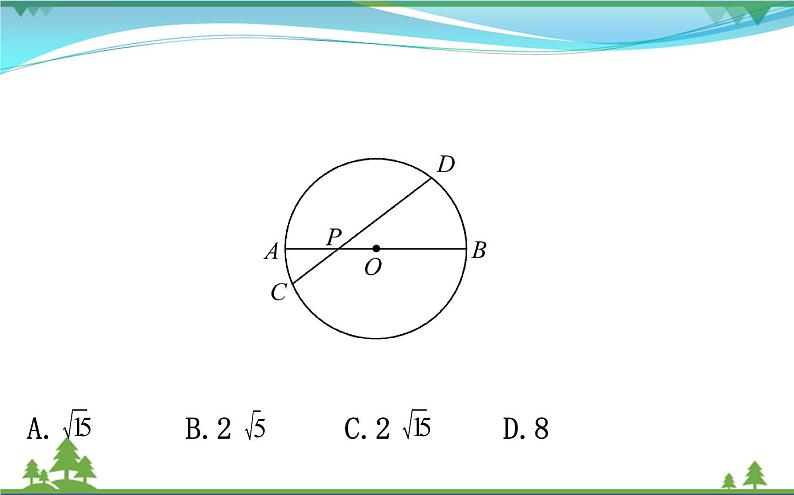
【核心突破】例1【原型题】(2018·枣庄中考)如图,AB是☉O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为(　 　 )
A. B.2 C.2 D.8
【变形题】(变换条件、结论)如图,AB是☉O的直径,弦CD交AB于点P,CP=3,DP=5,∠APC=45°,则AB的长为______. 
【明·技法】垂径定理运用中的“两注意”(1)两条辅助线:一是过圆心作弦的垂线,二是连接圆心和弦的一端(即半径),这样把半径、弦心距、弦的一半构建在一个直角三角形中,运用勾股定理求解.
(2)方程思想:在直接运用垂径定理求线段的长度时,常常将未知的一条线段设为x,利用勾股定理构造关于x的方程解决问题.这是一种用代数方法解决几何问题的解题思路.
【题组过关】1.(2019·武汉硚口区模拟)半径为10的☉O中,弦AB=16,则点O到弦AB的距离为(　 　)A.10B.8C.6D.5
2.(2019·北部湾中考)《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原
文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为_________寸.  
3.(易错警示题)在☉O中,半径为5,AB∥CD,且AB=6,CD=8,则AB,CD之间的距离为___________. 
4.如图是“明清影视城”的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20 cm,BD=200 cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助黄红同学计算出
这个圆弧形门的最高点离地面的高度是多少?世纪金榜导学号略
考点二　圆心角、弧、弦之间的关系【主干必备】圆心角、弧、弦之间的关系1.定理:在同圆或等圆中,相等的圆心角所对的弧___________,所对的弦也___________. 
2.推论:在同圆或等圆中,两个圆心角,两条弧,两条弦中如果有一组量___________,那么它们所对应的其余各组量都分别___________. 
【微点警示】(1)注意成立的条件:圆心角、弧、弦之间的关系定理及推论成立的大前提是“在同圆或等圆中”.(2)注意推出的依据:圆心角、弧、弦之间的关系定理及推论,都是来源于“圆的旋转不变性”.
【核心突破】 例2(2019·南京中考)如图,☉O的弦AB,CD的延长线相交于点P,且AB=CD.求证:PA=PC.
【思路点拨】连接AC,由圆心角、弧、弦的关系得出 ,进而得出 ,根据等弧所对的圆周角相等得出∠ACP=∠CAP,根据等角对等边证得结论.
【明·技法】圆中证明弦相等的两个思路(1)根据圆周角相等,得到弦相等.(2)根据弧相等,得到弦相等.
【题组过关】1.如图,AB,CD是☉O的直径, ,若∠AOE=32°,则∠COE的度数是(　 　)
A.32°B.60°C.68°D.64°
2.如图,在☉O中, 都是劣弧,且 ,那么弦AB、CD的数量关系是(　 　)
A.AB>2CD　　　　　B.AB=2CDC.AB<2CDD.AB,CD的大小无法确定
3.(2019·自贡中考)如图,☉O中,弦AB与CD相交于点E,AB=CD,连接AD,BC.
求证:(1) .(2)AE=CE.
【证明】(1)∵AB=CD,∴ ∴
(2)∵ ∴AD=BC,又∵∠ADE=∠CBE,∠DAE=∠BCE,∴△ADE≌△CBE(ASA),∴AE=CE.
考点三　圆周角定理及推论【主干必备】圆周角定理及推论1.定理:一条弧所对的圆周角等于它所对的圆心角的___________. 
2.推论:(1)半圆(或直径)所对的圆周角是___________,90°的圆周角所对的弦是___________. (2)同弧或等弧所对的圆周角___________. 
【微点警示】(1)圆心角与圆周角的区别:前者的顶点在圆心,后者的顶点在圆上.(2)等弧的含义:在同圆或等圆中能够互相重合的弧为等弧.
【核心突破】例3(2018·黑龙江中考)如图,AC为☉O的直径,点B在圆上,OD⊥AC交☉O于点D,连接BD,∠BDO=15°,则∠ACB=____________. 
【明·技法】圆中角的转化(1)解决与圆有关的角度的相关计算时,一般先判断角是圆周角还是圆心角,再转化成同弧所对的圆周角或圆心角,利用同弧所对的圆周角相等,同弧所对的圆周角是圆心角的一半等关系求解.
(2)在圆中当有直径这一条件时,往往要用到直径所对的圆周角是直角这一条件,若含45°角,可设法构造等腰直角三角形;若含30°或60°角,则设法构造含有30°角的直角三角形.
【题组过关】1.(2019·甘肃中考)如图,AB是☉O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=(　 　)
A.54°　　　B.64°　　　C.27°　　　D.37°
2.(2019·滨州中考)如图,AB为☉O的直径,C,D为☉O上两点,若∠BCD=40°,则∠ABD的大小为(　 　)
A.60°　　　　B.50°　　　　C.40°　　　　D.20°
3.(2019·连云港中考)如图,点A,B,C在☉O上,BC=6,∠BAC=30°,则☉O的半径为________. 
4.(综合训练题)如图,在平面直角坐标系中,已知☉A经过点E,B,C,O,且C(0,6),E(-8,0),O(0,0),则cs∠OBC的值为___. 
5.(2019·湖州模拟)在☉O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.略
考点四　圆内接四边形【主干必备】圆内接四边形的性质圆内接四边形的对角____________. 
【微点警示】(1)圆内接四边形的含义:四个顶点都在同一个圆上的四边形.(2)圆内接平行四边形:圆内接平行四边形对角相等且互补,可得四个角都是直角,因此它是矩形.
【核心突破】例4【原型题】(2019·镇江中考)如图,四边形ABCD是半圆的内接四边形,AB是直径, .若∠C=110°,则∠ABC的度数等于(　 　)
A.55°B.60°C.65°D.70°
【变形题】(变换条件、结论)如图,A,B,C三点都在☉O上,点D是AB延长线上一点,∠CBD=70°,则∠AOC的度数为(　 　)
A.55°B.70°C.110°D.140°
【明·技法】圆内接四边形的角的“两种”关系(1)对角互补:若四边形ABCD为☉O的内接四边形,则∠A+∠C=180°,∠B+∠D=180°.(2)任一外角与其相邻的内角的对角相等,简称圆内接四边形的外角等于其内对角.
【题组过关】1.(2019·宁波模拟)在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶3,则∠D的度数是(　 　)A.45°　　B.60°　　C.90°　　D.135°
2.(2019·兰州中考)如图,四边形ABCD内接于☉O,若∠A=40°,则∠C=(　 　)
A.110°　　　　　　B.120°C.135°D.140°
3.如图AB为☉O的直径,弦CD⊥AB,垂足为点E,K为 上一动点,AK,DC的延长线相交于点F,连接CK,KD.
(1)求证:∠AKD=∠CKF.(2)若AB=10,CD=6,求tan∠CKF的值.