





中考数学全程复习方略 第26讲 与圆有关的位置关系 课件
展开考点一 点与圆的位置关系【主干必备】点与圆的位置关系1.设圆O的半径为r,点P到圆心的距离为OP=d.则:(1)点P在圆外⇔__________;
(2)点P在圆上⇔__________; (3)点P在圆内⇔__________.
2.确定圆的条件:不在同一条直线上的三个点确定___________圆.
【微点警示】(1)注意互逆:由点和圆的位置关系可以推得d与r的大小关系;反之,由d与r的大小关系也可以推得点和圆的位置关系.(2)注意条件:三个点确定一个圆的前提是这三个点不在同一直线上.
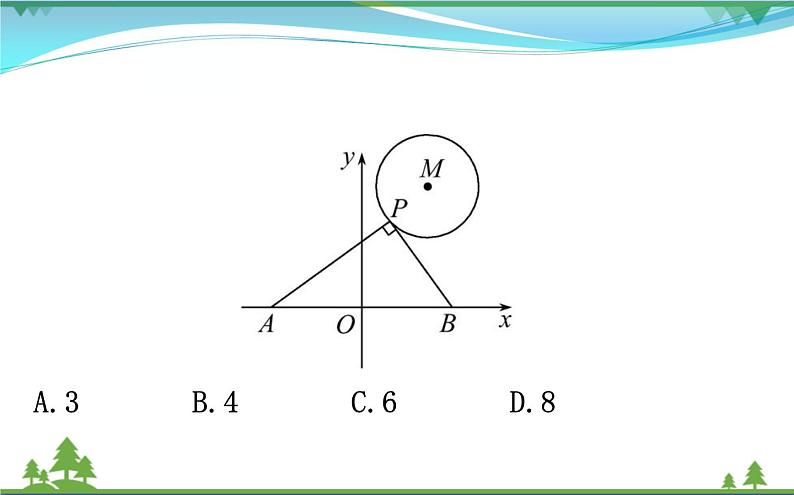
【核心突破】例1(2018·泰安中考)如图,☉M的半径为2,圆心M的坐标为(3,4),点P是☉M上的任意一点,PA⊥PB,且PA,PB与x轴分别交于A,B两点,若点A,点B关于原点O对称,则AB的最小值为( )
A.3B.4C.6D.8
【明·技法】圆外一点到圆上各点的距离的最值(1)最短距离= 圆外一点与圆心的距离-半径.(2)最长距离=圆外一点与圆心的距离+半径.
【题组过关】1. (2019·上海金山区模拟)如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( )
A.点B,点C都在☉A内B.点C在☉A内,点B在☉A外C.点B在☉A内,点C在☉A外D.点B,点C都在☉A外
2.(易错警示题)在直角坐标平面内,点O是坐标原点,点A的坐标是(3,2),点B的坐标是(3,-4).如果以点O为圆心,r为半径的圆O与直线AB相交,且点A,B中有一点在圆O内,另一点在圆O外,那么r的值可以取( )A.5B.4C.3D.2
3.(2019·江都区模拟)有一张矩形的纸片,AB=6 cm,AD=8 cm,若以A为圆心作圆,并且要使点B在☉A内,而点C在☉A外,☉A的半径r的取值范围是____________________.
考点二 直线与圆的位置关系【主干必备】设圆的半径为r,圆心到直线的距离为d.
【微点警示】(1)注意互逆:由直线和圆的位置关系可以推得d与r的大小关系;反之,由d与r的大小关系也可以推得直线和圆的位置关系.
(2)“d”的不同:点与圆的位置关系中,“d”是指两点之间的距离;直线与圆的位置关系中,“d”是指点与直线的距离.
【核心突破】例2(2019·菏泽中考)如图,直线y= -3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是_____________.
【明·技法】判断直线与圆位置关系的两种方法1.用直线与圆交点的个数来判断.2.用圆心到直线的距离与半径的大小来判断.
【题组过关】1.(易错警示题)已知☉O的半径为4,直线l上有一点P与☉O的圆心的距离为4,则直线l与☉O的位置关系为 ( )A.相离 B.相切C.相交D.相切、相交均有可能
2.(2019·杭州上城区模拟)已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的☉O与射线AC有公共点,那么x的取值范围是 ( )A.0
3.(2019·玄武区模拟)直径为10 cm的圆,若该圆的圆心到直线的距离为4 cm,则该直线与圆的公共点个数为________.
4.(2019·达州中考)如图,☉O是△ABC的外接圆,∠BAC的平分线交☉O于点D,交BC于点E,过点D作直线DF∥BC.
(1)判断直线DF与☉O的位置关系,并说明理由;(2)若AB=6,AE= ,CE= ,求BD的长.
【解析】(1) DF与☉O相切,理由:连接OD,
∵∠BAC的平分线交☉O于点D,∴∠BAD=∠CAD,∴ ,∴OD⊥BC,∵DF∥BC,∴OD⊥DF,∴DF与☉O相切.
(2)∵∠BAD=∠CAD,∠ADB=∠C,∴△ABD∽△AEC,∴ ,∴ ,∴BD= .
考点三 切线的性质与判定【主干必备】1.切线的定义、性质与判定(1)定义:和圆有___________公共点的直线. (2)性质:圆的切线_____________过切点的半径.
(3)判定:经过半径的外端,并且___________于这条半径的直线是圆的切线.
2.切线长定理从圆外一点可以引圆的两条切线,它们的切线长___________,这一点和圆心的连线___________两条切线的夹角.
【微点警示】(1)注意性质与判定的区别:知切线推得“垂直”是性质,知“垂直”推得切线是判定.(2)注意“切线长”的含义:圆的切线是直线,本无长度,“切线长”专指圆外一点和切点之间的线段的长度.
【核心突破】例3(2019·菏泽中考)如图,BC是☉O的直径,CE是☉O的弦,过点E作☉O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.
(1)求证:∠ABG=2∠C.(2)若GF=3 ,GB=6,求☉O的半径.
【思路点拨】(1)连接OE,根据切线的性质得到OE⊥EG,推出OE∥AB,得到∠A=∠OEC,根据等腰三角形的性质得到∠OEC=∠C,求得∠A=∠C,根据三角形的外角的性质即可得到结论.(2)根据勾股定理得到BF= =3,根据相似三角形的性质即可得到结论.
【自主解答】(1)连接OE,∵EG是☉O的切线,∴OE⊥EG,∵BF⊥GE,∴OE∥AB,
∴∠A=∠OEC,∵OE=OC,∴∠OEC=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C.
例4【原型题】(2019·凉山州中考)如图,点D是以AB为直径的☉O上一点,过点B作☉O的切线,交AD的延长线于点C,E是BC的中点,连接DE并延长与AB的延长线交于点F.
(1)求证:DF是☉O的切线.(2)若OB=BF,EF=4,求AD的长.
【变形题】(变换条件、结论)如图,在△ABC中,AB=AC,以AB为直径的☉O交BC边于点D,交AC边于点E.过点D作☉O的切线,交AC于点F,交AB的延长线于点G,连接DE.
(1)求证:BD=CD.(2)若∠G=40°,求∠AED的度数.
【解析】(1)连接AD,∵AB为直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴BD=CD.(2)略
【明·技法】与圆的切线有关的三种辅助线(1)若已知直线与圆相切,先连接圆心和切点,根据切线性质得到直角,再作进一步的计算或推理,可简述为:见切线,连半径,得垂直.
(2)若已知直线与圆的公共点,证该直线为圆的切线,则采用判定定理法,其基本思路是:当已知点在圆上时,连接过这点的半径,证明这条半径与直线垂直即可,可简述为:有公共点,连半径,证垂直,得切线.
(3)若未知直线与圆的交点,证该直线为圆的切线,则采用数量关系法,其基本思路是:过圆心作直线的垂线段,证明垂线段的长等于圆的半径,可简述为:无公共点,作垂线,证半径,得切线.
【题组过关】1.(2019·无锡中考)如图,PA是☉O的切线,切点为A,PO的延长线交☉O于点B,若∠P=40°,则∠B的度数为 ( )
A.20° B.25° C.40° D.50°
2.(2019·石家庄市桥西区模拟)如图,AB是☉O的直径,点P是☉O外一点,PO交☉O于点C,连接BC,PA.若∠P=40°,当∠B等于____________时,PA与☉O相切世纪金榜导学号( )
A.20° B.25° C.30° D.40°
3.(2019·菏泽东明县模拟)如图,PA,PB切☉O于点A,B,PA=10,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是( )
A.10B.18C.20D.22
4.(2019·河南模拟)如图,已知AB是☉O的直径,AD,BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD= ,则PA的长为________.
5.(2019·天水中考)如图,AB,AC分别是☉O的直径和弦,OD⊥AC于点D.过点A作☉O的切线与OD的延长线交于点P,PC,AB的延长线交于点F.
(1)求证:PC是☉O的切线.(2)若∠ABC=60°,AB=10,求线段CF的长.
【解析】(1)连接OC,∵OD⊥AC,OD经过圆心O,∴AD=CD,∴△PDA≌△PDC,∴PA=PC.
在△OAP和△OCP中,∵ ∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP.∵PA是☉O的切线,∴∠OAP=90°,∴∠OCP=90°,即OC⊥PC,∴PC是☉O的切线.(2)略
考点四 三角形的外接圆与内切圆【主干必备】
【微点警示】(1)三角形外心与内心的位置:锐角三角形的外心在其内部,直角三角形的外心在其斜边上,钝角三角形的外心在其外部;而任意三角形的内心都在其内部.(2)等边三角形的外心与内心:等边三角形的外接圆与内切圆是同心圆,即等边三角形的外心与内心合二为一.
【核心突破】例5(2018·长沙中考)如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长.(2)求证:△ABC为等腰三角形.(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
【思路点拨】(1)证明AD为△BCE的中位线得到CE=2AD=6.(2)通过证明AC=AE得到AB=AC.
(3)取△ABC的外心点P,内心点Q,连接BP,BQ,CQ,先利用勾股定理计算出AB=5,设☉P的半径为R,☉Q的半径为r,在Rt△PBD中利用勾股定理得到(R-3)2+42=R2,解得R= ,则PD= ,再利用面积法求出r= ,即QD= ,然后计算PD+QD即可.
【明·技法】与三角形的外心与内心有关的解题技巧(1)连接外心与三角形各顶点,可得等腰三角形.(2)连接内心与三角形顶点的连线平分这个内角.
【题组过关】1.(易错警示题)如图,点I是△ABC的内心,若∠AIB=125°,则∠C等于( )
A.65°B.70°C.75°D.80°
2.(2019·荆门中考)如图,△ABC的内心为I,连接AI并延长交△ABC的外接圆于D,则线段DI与DB的大小关系是( )
A.DI=DB B.DI>DBC.DI
4. (2019·荆门中考)已知锐角△ABC的外接圆圆心为O,半径为R.
(1)求证: =2R.(2)若在△ABC中∠A=45°,∠B=60°,AC= ,求BC的长及sin C的值.
【解析】(1)连接AO并延长交圆于D点,连接CD,
∵AD为直径, ∴∠ACD=90°,且∠ABC=∠ADC.在Rt△ACD中sin∠ABC=sin∠ADC= ,∴ =2R.
(2)由(1)知 =2R,同理可得 =2R.∴2R= =2,∴BC=2R·sin∠BAC=2sin 45°= ,如图,作CE⊥AB,垂足为E,
中考数学全程复习方略 第25讲 圆的认识 课件: 这是一份中考数学全程复习方略 第25讲 圆的认识 课件,共59页。PPT课件主要包含了轴对称图形,径所在直线,平分弦,两条弧,垂直于弦,1或7,自主解答略等内容,欢迎下载使用。
中考数学全程复习方略 第10讲 函数初步 课件: 这是一份中考数学全程复习方略 第10讲 函数初步 课件,共60页。PPT课件主要包含了有序实数对,互为相反数,x-y,-xy,-x-y,唯一确定,x≥2且x≠3,横坐标,纵坐标等内容,欢迎下载使用。
中考数学全程复习方略 第4讲 分式 课件: 这是一份中考数学全程复习方略 第4讲 分式 课件,共60页。PPT课件主要包含了公因式,基本性质,同分母,自主解答,解析原式等内容,欢迎下载使用。












