中考数学全程复习方略 微专题五 图形变换中的最值问题 课件

这是一份中考数学全程复习方略 微专题五 图形变换中的最值问题 课件，共21页。

【主干必备】1.解决图形变换中最值问题的两种数学模型:(1)线段的基本事实:两点之间_________最短. (2)垂线段的性质:垂线段_________. 
2.解决图形变换中最值问题的三种变换方式:(1)对称变换是解决最值问题的常用手段:通过点的对称变换可以达到线段_________不变,线段_________改变的效果. 
如图,在直线l上的同侧有两个点A,B,在直线l上找到A,B的距离之和最短的点,可以作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点就是所要找的点.
(2)平移变换是解决最值问题的重要手段:通过平移变换可实现线段_________变换,线段_________、_____不变. (3)旋转变换是解决最值问题的手段之一:旋转变换是将一个图形在不改变_________和_________的前提下,改变原来的_________. 
【微点警示】图形变换的目的:改变图形位置,优化图形结构,整合图形信息,转化为基本模型.
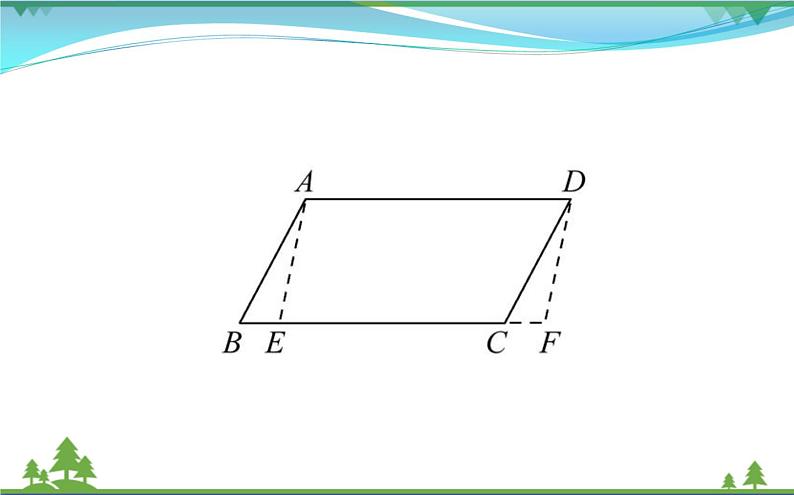
【核心突破】 【类型一】应用“垂线段最短”解决最值问题 例1(2018·长春中考)如图,在▱ABCD中,AD=7,AB=2 ,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为_______. 
【类型二】应用“两点之间线段最短”解决最值问题例2(2018·滨州中考)如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是(　 　)
A. 　　　　B. 　　　　C.6　　　　D.3
【类型三】综合应用“垂线段最短”和“两点之间线段最短”解决最值问题例3(2018·自贡中考)如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是___　形,点P,E,F分别为线段AB,AD,DB上的任意点,则PE+PF的最小值是_____. 
【明·技法】解决图形变换中最值问题的方法选择(1)平移或旋转变换中的最值问题,一般作出垂线段,运用“垂线段最短”去解决.(2)圆弧轨迹问题中的最值问题,一般连接定点和圆心,与圆弧交点便是所求点.
(3)动点问题中的最值问题,一般作出点关于动点所在直线的对称点,结合轴对称的知识和“垂线段最短”分析得出最短路径.
【题组过关】1.(生活情境题)木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是(　 　)
2.(2019·长沙中考)如图,在△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+ BD的最小值是(　 　)
A.2 　　　B.4 　　　C.5 　　　D.10
3.(2019·宿迁中考)如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为______.