2021中考数学压轴题题型：专题13二次函数与交点公共点综合问题（含原卷及解析卷）

这是一份2021中考数学压轴题题型：专题13二次函数与交点公共点综合问题（含原卷及解析卷），文件包含二次函数与交点公共点综合问题原卷版docx、二次函数与交点公共点综合问题解析版docx等2份学案配套教学资源，其中学案共75页， 欢迎下载使用。

2021新版中考数学压轴题之学霸秘笈大揭秘
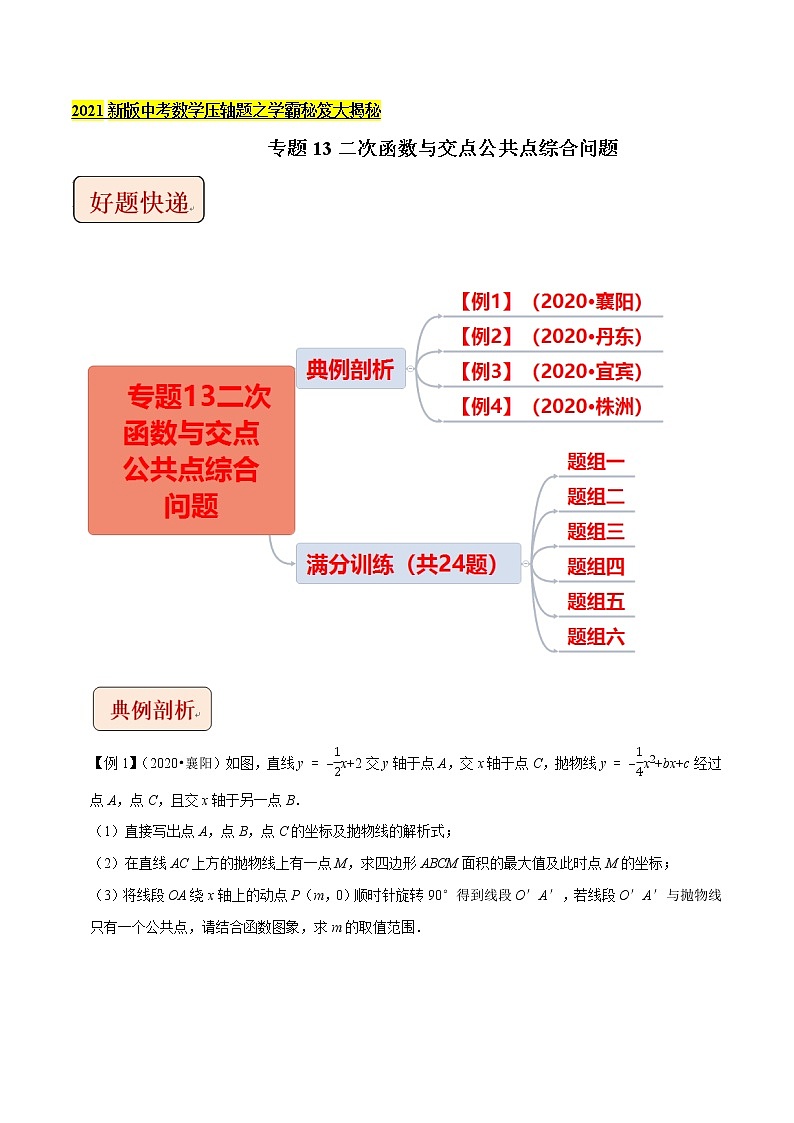
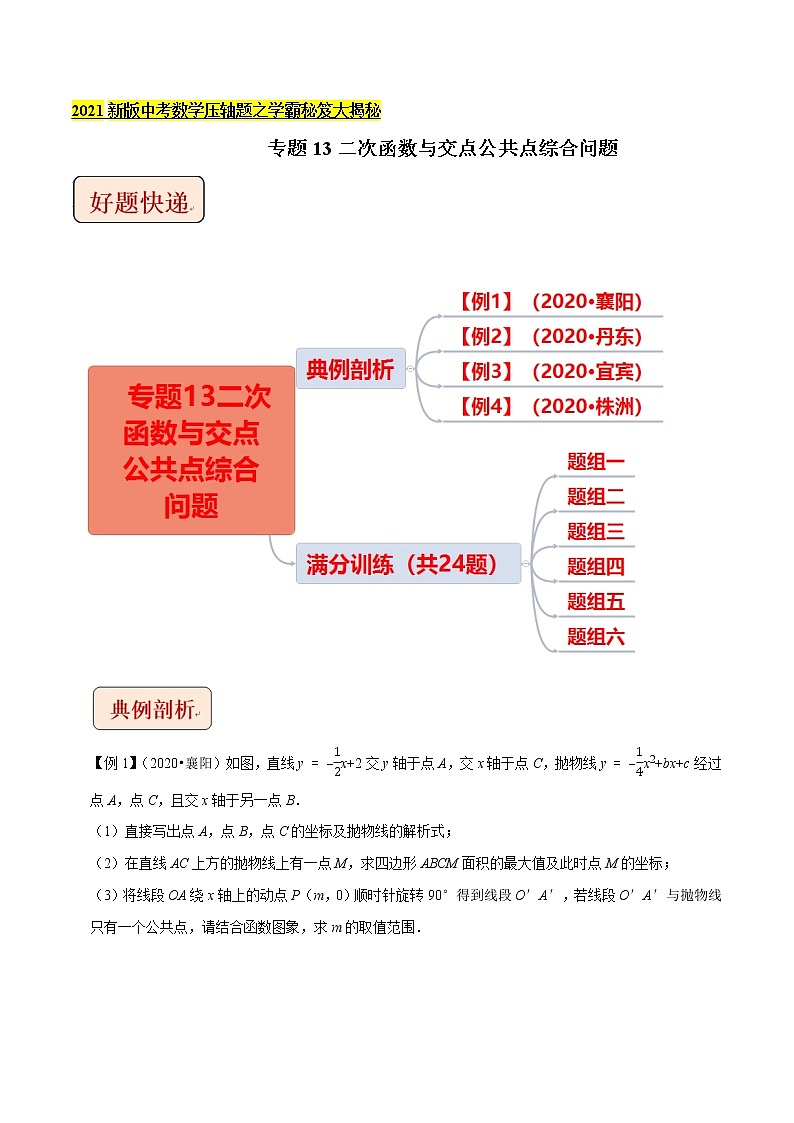
专题13二次函数与交点公共点综合问题


【例1】（2020•襄阳）如图，直线y=−12x+2交y轴于点A，交x轴于点C，抛物线y=−14x2+bx+c经过点A，点C，且交x轴于另一点B．
（1）直接写出点A，点B，点C的坐标及拋物线的解析式；
（2）在直线AC上方的抛物线上有一点M，求四边形ABCM面积的最大值及此时点M的坐标；
（3）将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O′A′，若线段O′A′与抛物线只有一个公共点，请结合函数图象，求m的取值范围．

【分析】（1）令x＝0，由y=−12x+2，得A点坐标，令y＝0，由y=−12x+2，得C点坐标，将A、C的坐标代入抛物线的解析式便可求得抛物线的解析式，进而由二次函数解析式令y＝0，便可求得B点坐标；
（2）过M点作MN⊥x轴，与AC交于点N，设M（a，−14a2+12a+2），则N（a，−12a+2），由三角形的面积公式表示出四边形的面积关于a的函数关系式，再根据二次函数的性质求得最大值，并求得a的值，便可得M点的坐标；
（3）根据旋转性质，求得O′点和A′点的坐标，令O′点和A′点在抛物线上时，求出m的最大和最小值便可．
【解析】（1）令x＝0，得y=−12x+2＝2，
∴A（0，2），
令y＝0，得y=−12x+2＝0，解得，x＝4，
∴C（4，0），
把A、C两点代入y=−14x2+bx+c得，
c=2−4+4b+c=0，解得b=12c=2，
∴抛物线的解析式为y=−14x2+12x+2，
令y＝0，得y=−14x2+12x+2=0，
解得，x＝4，或x＝﹣2，
∴B（﹣2，0）；

（2）过M点作MN⊥x轴，与AC交于点N，如图1，
设M（a，−14a2+12a+2），则N（a，−12a+2），
∴S△ACM=12MN⋅OC=12(−14a2+a)×4=−12a2+2a，
∵S△ABC=12BC⋅OA=12×(4+2)×2=6，
∴S四边形ABCM＝S△ACM+S△ABC=−12a2+2a+6=−12(a−2)2+8，
∴当a＝2时，四边形ABCM面积最大，其最大值为8，
此时M的坐标为（2，2）；


（3）∵将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O′A′，如图2，

∴PO′＝PO＝m，O′A′＝OA＝2，
∴O′（m，m），A′（m+2，m），
当A′（m+2，m）在抛物线上时，有−14(m+2)2+12(m+2)+2=m，
解得，m＝﹣3±17，
当点O′（m，m）在抛物线上时，有−14m2+12m+2=m，
解得，m＝﹣4或2，
∴当﹣3−17≤m≤﹣4或﹣3+17≤m≤2时，线段O′A′与抛物线只有一个公共点．
【例2】（2020•丹东）如图1，在平面直角坐标系中，抛物线y=−12x2+bx+c与x轴交于A，B两点，A点坐标为（﹣2，0），与y轴交于点C（0，4），直线y=−12x+m与抛物线交于B，D两点．
（1）求抛物线的函数表达式．
（2）求m的值和D点坐标．
（3）点P是直线BD上方抛物线上的动点，过点P作x轴的垂线，垂足为H，交直线BD于点F，过点D作x轴的平行线，交PH于点N，当N是线段PF的三等分点时，求P点坐标．
（4）如图2，Q是x轴上一点，其坐标为（−45，0）．动点M从A出发，沿x轴正方向以每秒5个单位的速度运动，设M的运动时间为t（t＞0），连接AD，过M作MG⊥AD于点G，以MG所在直线为对称轴，线段AQ经轴对称变换后的图形为A′Q′，点M在运动过程中，线段A′Q′的位置也随之变化，请直接写出运动过程中线段A′Q′与抛物线有公共点时t的取值范围．

【分析】（1）利用待定系数法解决问题即可．
（2）求出点B的坐标，可得直线BD的解析式，构建方程组确定点D坐标即可．
（3）设P（a，−12a2+a+4），则N（a，52），F（a，−12a+2）推出PN=−12a2+a+4−52=−12a2+a+32，NF=52−（−12a+2）=12a+12，由N是线段PF的三等分点，推出PN＝2NF或NF＝2PN，构建方程求解即可．
（4）首先证明QQ′∥AD，由题意直线QQ′的解析式为y=52x+2，设直线QQ′交抛物线于E，利用方程组求出点E的坐标，求出两种特殊情形t的值即可判断．
【解析】（1）把A（﹣2，0），C（0，4）代入y=−12x2+bx+c，
得到c=4−2−2b+c=0，
解得b=1c=4，
∴抛物线的解析式为y=−12x2+x+4．

（2）令y＝0，则有−12x2+x+4＝0，
解得x＝﹣2或4，
∴B（4，0），
把B（4，0）代入y=−12x+m，得到m＝2，
∴直线BD的解析式为y=−12x+2，
由y=−12x2+x+4y=−12x+2，解得x=4y=0或x=−1y=52，
∴D（﹣1，52）．

（3）设P（a，−12a2+a+4），
则N（a，52），F（a，−12a+2），
∴PN=−12a2+a+4−52=−12a2+a+32，NF=52−（−12a+2）=12a+12，
∵N是线段PF的三等分点，
∴PN＝2NF或NF＝2PN，
∴−12a2+a+32=a+1或12a+12=−a2+2a+3，
解得a＝±1或﹣1或52，
∵a＞﹣1，
∴a＝1或52，
∴P（1，92）或（52，278）．

（4）如图2中，

∵A（﹣2，0），D（﹣1，52），
∴直线AD的解析式为y=52x+5，
∵A′Q′与AQ关于MG对称，MG⊥AD，
∴QQ′∥AD，
∵Q（−45，0），
∴直线QQ′的解析式为y=52x+2，设直线QQ′交抛物线于E，
由y=−12x2+x+4y=52x+2，解得x=1y=92或x=−4y=−8，
∴E（1，92），
当点A′与D重合时，直线GM的解析式为y=−25x+1320，可得M（138，0），此时t=2940，
当点Q′与E重合时，直线GM经过点（110，94），
∵GM⊥AD，
∴GM的解析式为y=−25x+229100，
令y＝0，可得x=22940，
∴M（22940，0），此时t=2272+2522940+25=309200，
观察图象可知，满足条件的t的值为2940≤t≤309200．
【例3】（2020•宜宾）如图，已知二次函数的图象顶点在原点，且点（2，1）在二次函数的图象上，过点F（0，1）作x轴的平行线交二次函数的图象于M、N两点．
（1）求二次函数的表达式；
（2）P为平面内一点，当△PMN是等边三角形时，求点P的坐标；
（3）在二次函数的图象上是否存在一点E，使得以点E为圆心的圆过点F和点N，且与直线y＝﹣1相切．若存在，求出点E的坐标，并求⊙E的半径；若不存在，说明理由．

【分析】（1）设二次函数表达式为：y＝ax2，将（2，1）代入上式，即可求解；
（2）△PMN是等边三角形，则点P在y轴上且PM＝4，故PF＝23，即可求解；
（3）在Rt△FQE中，EN=(2−1)2+(1−14)2=54，EF=(1−0)2+(1−14)2=54，即可求解．
【解析】（1）∵二次函数的图象顶点在原点，
故设二次函数表达式为：y＝ax2，将（2，1）代入上式并解得：a=14，
故二次函数表达式为：y=14x2；

（2）将y＝1代入y=14x2并解得：x＝±2，故点M、N的坐标分别为（﹣2，1）、（2，1），
则MN＝4，
∵△PMN是等边三角形，
∴点P在y轴上且PM＝4，
∴PF＝23；
∵点F（0，1），
∴点P的坐标为（0，1+23）或（0，1﹣23）；

（3）假设二次函数的图象上存在一点E满足条件，
设点Q是FN的中点，则点Q（1，1），
故点E在FN的中垂线上．
∴点E是FN的中垂线与y=14x2图象的交点，
∴y=14×12=14，则点E（1，14），
EN=(2−1)2+(1−14)2=54，
同理EF=(1−0)2+(1−14)2=54，
点E到直线y＝﹣1的距离为|14−（﹣1）|=54，
故存在点E，使得以点E为圆心半径为54的圆过点F，N且与直线y＝﹣1相切．
【例4】（2020•株洲）如图所示，二次函数y＝ax2+bx+c（a＞0）的图象（记为抛物线L）与y轴交于点C，与x轴分别交于点A、B，点A、B的横坐标分别记为x1，x2，且0＜x1＜x2．
（1）若a＝c，b＝﹣3，且过点（1，﹣1），求该二次函数的表达式；
（2）若关于x的一元二次方程ax2+bx+c＝0的判别式△＝4．求证：当b＜−52时，二次函数y1＝ax2+（b+1）x+c的图象与x轴没有交点．
（3）若AB2=c2−2c+6c，点P的坐标为（−x0，﹣1），过点P作直线l垂直于y轴，且抛物线的L的顶点在直线l上，连接OP、AP、BP，PA的延长线与抛物线L交于点D，若∠OPB＝∠DAB，求x0的最小值．

【分析】（1）根据题意，把a＝c，b＝﹣3，点（1，﹣1），代入解析式，即可求出解析式；
（2）利用根的判别式进行判断，即可得到结论；
（3）根据二次函数的性质，得到b2﹣4ac＝4a，结合根与系数的关系，得到4a=c2−2c+6c，然后证明△OAP∽△OPB，得到OAOP=OPOB，然后得到x0=ca−1，利用二次函数的性质即可得到答案．
【解析】（1）由题意得：y＝ax2﹣3x+a，
∵函数过点（1，﹣1），
∴a﹣3+a＝﹣1，
∴a＝c＝1，
∴y＝x2﹣3x+1；

（2）由题意，一元二次方程ax2+bx+c＝0的判别式△＝4．
∴△＝b2﹣4ac＝4，
∴4ac＝b2﹣4，
在函数y1=ax2+(b+1)x+c中，△1=(b+1)2−4ac=(b+1)2−(b2−4)=2b+5，
∵b＜−52，
∴2b+5＜0，
即函数图象与x轴没有交点；

（3）因为函数顶点在直线l上，则有4ac−b24a=−1，
即b2﹣4ac＝4a①，
∵AB2=c2−2c+6c，
∴(x2−x1)2=c2−2c+6c，
即(x1+x2)2−4x1x2=c2−2c+6c，
∴b2−4aca2=c2−2c+6c，
由①得：4a=c2−2c+6c②，
∵∠OAP＝∠DAB，∠OPB＝∠DAB，
∴∠OAP＝∠OPB，
∵∠OAP＝∠OBP+∠APB，∠OPB＝∠OPA+∠APB，
∴∠OBP＝∠OPA，
则△OAP∽△OPB．
∴OAOP=OPOB，
∴OA•OB＝OP2，
∴x1x2=(−x0)2+(−1)2．
∴ca=x0+1，
∴x0=ca−1．
由②得：x0=c2−2c+64−1，
∴x0=14(c−1)2+14，
∴当c＝1时，(x0)min=14．


【题组一】
1．（2020•滨湖区模拟）如图，在平面直角坐标系中，直线y=12x﹣2与x轴交于点A，与y轴交于点C，抛物线y=12x2+bx+c经过A、C两点，与x轴的另一交点为点B．
（1）求抛物线的函数表达式；
（2）点D为直线AC下方抛物线上一动点；
①连接CD，是否存在点D，使得AC平分∠OCD？若存在，求点D的横坐标；若不存在，请说明理由．
②在①的条件下，若点P为抛物线上位于AC下方的一个动点，以P、C、A、D为顶点的四边形面积记作S，则S取何值或在什么范围时，相应的点P有且只有两个？

【分析】（1）先求出直线与坐标轴的交点A、C的坐标，再用待定系数法求得抛物线的解析式；
（2）①作点O关于直线AC的对称点F，过F作FG⊥y轴于点G，延长CF与抛物线交于点D，此时∠ACO＝∠ACD，即AC平分∠OCD，由三角形面积公式求得OE，进而求得OF，再证明△OAC∽△GOF，便可求得F点的坐标，进而求得直线CF的解析式，最后求得直线CF与抛物线的交点坐标便可；
②需要分类讨论：点P在OC的左侧、右侧两种情况．利用分割法求得S的值，进行比较即可得到答案．
【解析】（1）令x＝0，得y=12x﹣2＝﹣2，
令y＝0，得y=12x﹣2＝0，解得x＝4，
∴A（4，0），C（0，﹣2），
把A（4，0），C（0，﹣2）代入y=12x2+bx+c中，得
12×16+4b+c=0c=−2，
解得，b=−32c=−2，
∴抛物线的函数表达式为y=12x2−32x﹣2；
（2）①作点O关于直线AC的对称点F，过F作FG⊥y轴于点G，延长CF与抛物线交于点D，
此时∠ACO＝∠ACD，即AC平分∠OCD，

∵OA＝4，OC＝2，
∴AC＝25，
∵OF⊥AC，
∴OE=OA⋅OCAC=455，
∴OF=2OE=855，
∵∠COE+∠ACO＝∠COE+OFG＝90°，
∴∠ACO＝∠OFG，
∵∠AOC＝∠OGF＝90°，
∴△OAC∽△GOF，
∴OCGF=OAGO=ACOF，即2GF=4OG=25855，
∴GF=85，OG=165，
∴F（85，−165），
设直线CF的解析式为y＝kx+b（k≠0），则
85k+b=−165b=−2，
解得，k=−34b=−2，
∴直线CF的解析式为：y=−34x−2，
联立方程组y=−34x−2y=12x2−32x−2，
解得，x1=0y1=−2，x2=32y2=−258，
∴存在点D，使得AC平分∠OCD，点D的横坐标为32；
②设P（x，12x2−32x﹣2）．
若点P在D点的左侧，如图2，过D作DE⊥x轴于E，连接OP，CP，PE，PD，AD，

S＝S△OCP+S△OPE+S△PDE+S△ADE﹣S△OAC
=12×2x+12×32(−12x2+32x+2)+12×258(32−x)+12×（4−32）×258−12×4×2
=−38（x−34）2+247128，
∴当x=34时，S取最大值为247128，
若点P在D点的右侧，如图3，过D作DE⊥x轴于点E，连接CD，DP，PE，PA．

S＝S梯形OCDE+S△PDE+S△APE﹣S△AOC
=12(2+258)×32+12×258(x−32)+12×(4−32)(−12x2+32x+2)−12×4×2
=−58（x−114）2+605128，
∴当x=114时，S取最大值为605128，
综上，根据抛物线的对称性质可知，当247128＜S＜605128时，P点有且只有两个．
2．（2019秋•乐亭县期末）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）．抛物线的解析式为y＝ax2+bx．
（1）如图1，若抛物线经过A，D两点，直接写出A点的坐标　（4，8）　；抛物线的对称轴为直线　6　；
（2）如图2：①若抛物线经过A、C两点，求抛物线的表达式．
②若点P为线段AB上一动点，过点P作PE⊥AB交AC于点E，过点E作EF⊥AD于点F交抛物线于点G．当线段EG最长时，求点E的坐标；
（3）若a＝﹣1，且抛物线与矩形ABCD没有公共点，直接写出b的取值范围．

【分析】（1）点A的坐标为：（4，8）；函数的对称轴为：x=12（4+8）＝6；
（2）①将点A、C的坐标代入抛物线表达式并解得：a=−12，b＝4，即可求解；
②由点A、C的坐标得，直线AC的表达式为：y＝﹣2x+16；EG=−12x2+4x﹣（﹣2x+16）=−12x2+6x﹣16，即可求解；
（3）若a＝﹣1，则抛物线的表达式为：y＝﹣x2+bx，当抛物线过点B和点D时，抛物线与矩形有一个交点，即可求解．
【解析】（1）点A的坐标为：（4，8）；函数的对称轴为：x=12（4+8）＝6；
故答案为：（4，8）；6；

（2）①将点A、C的坐标代入抛物线表达式并解得：a=−12，b＝4，
故抛物线的表达式为：y=−12x2+4x；
②由点A、C的坐标得，直线AC的表达式为：y＝﹣2x+16；
设点E（x，﹣2x+16），则点G（x，−12x2+4x），
EG=−12x2+4x﹣（﹣2x+16）=−12x2+6x﹣16，
当x＝6时，EG由最大值为：2，此时点E（6，4）；

（3）若a＝﹣1，则抛物线的表达式为：y＝﹣x2+bx，
当抛物线过点B和点D时，抛物线与矩形有一个交点，
将点B的坐标代入抛物线表达式得：0＝﹣16+4b，解得：b＝4，
将点D的坐标代入抛物线表达式并解得：b＝9，
故b的取值范围为：b＜4或b＞9．
3．（2020•姜堰区二模）二次函数y=m6x2−2m3x+m（m＞0）的图象交y轴于点A，顶点为P，直线PA与x轴交于点B．
（1）当m＝1时，求顶点P的坐标；
（2）若点Q（a，b）在二次函数y=m6x2−2m3x+m（m＞0）的图象上，且b﹣m＞0，试求a的取值范围；
（3）在第一象限内，以AB为边作正方形ABCD．
①求点D的坐标（用含m的代数式表示）；
②若该二次函数的图象与正方形ABCD的边CD有公共点，请直接写出符合条件的整数m的值．

【分析】（1）当m＝1时，y=m6x2−2m3x+m=16（x﹣2）2+13，即可求解；
（2）对于y=m6x2−2m3x+m，令x＝0，则y＝m，即点A（0，m），b﹣m＞0，即点Q在点A的上方，即可求解；
（3）①证明△AOB≌△DHA（AAS），则HD＝AO＝m，AH＝BO＝3，即可求解；②分x＝m、m≥5、m≥2三种情况，即可求解．
【解析】（1）当m＝1时，y=m6x2−2m3x+m=16（x﹣2）2+13，
故点P（2，13）；

（2）对于y=m6x2−2m3x+m，令x＝0，则y＝m，即点A（0，m），
∵b﹣m＞0，即点Q在点A的上方，
而抛物线的对称轴为x＝2，故点A关于对称轴的对称点的横坐标为4，
故a的取值范围为：a＜0或a＞4；


（3）①由抛物线的表达式知，点P（2，13m），
由点A（0，m）和点P的坐标得，直线PA的表达式为y=−13mx+m，
令y=−13mx+m＝0，解得x＝3，故点B（3，0），
过点D作DH⊥y轴于点H，
∵∠HAD+∠HDA＝90°，∠HAD+∠OAB＝90°，
∴∠OAB＝∠HDA，
∵∠AOB＝∠DHA＝90°，AD＝AB，
∴△AOB≌△DHA（AAS），
∴HD＝AO＝m，AH＝BO＝3，
故D（m，m+3）；
②同①的方法得，C（m+3，3），
∵二次函数的图象与正方形ABCD的边CD有公共点，
∴当x＝m时，y≤m+3，可得m36−2m23+m≤m+3，
化简得：m3﹣4m2≤18．
∵m＞0，
∴m2−4m≤18m，
∴(m−2)2−4≤18m，
显然：m＝1，2，3，4是上述不等式的解，
当m≥5时，（m﹣2）2﹣4≥5，18m≤3.6，此时，(m−2)2−4＞18m，
∴符合条件的正整数m＝1，2，3，4；
当x＝m+3时，y≥3，可得m(m+3)26−2m(m+3)6+m≥3，
∵m＞0，
∴m2+2m+3≥18m，即(m+1)2+2≥18m，
显然：m＝1不是上述不等式的解，
当m≥2时，（m+1）2+2≥11，18m≤9，此时，(m+1)2+2＞18m恒成立，
∴符合条件的正整数m＝2，3，4；
综上：符合条件的正整数m的值为2，3，4．
4．（2020•天心区模拟）如图，抛物线y=−845(x+1538)（x﹣3m）（其中m＞0）与x轴分别交于A、B两点（A在B的右侧），与y轴交于点C；
（1）点B的坐标为　（−1538，0）　，点A的坐标为　（3m，0）　（用含m的代数式表示），点C的坐标为　（0，3m）　（用含m的代数式表示）；
（2）若点P为直线AC上的一点，且点P在第二象限，满足OP2＝PC•PA，求tan∠APO的值及用含m的代数式表示点P的坐标；
（3）在（2）的情况下，线段OP与抛物线相交于点Q，若点Q恰好为OP的中点，此时对于在抛物线上且介于点C与顶点之间（含点C与顶点）的任意一点M（x0，y0）总能使不等式n≤43x0+23316及不等式2n−916≥−4x02+3x0+138恒成立，求n的取值范围．

【分析】（1）分别令x＝0和y＝0，即可求解；
（2）根据特殊三角函数值可得∠CAO＝30°，证明△OPA∽△CPO，则∠POC＝∠OAC＝30°，可得tan∠APO=33，过P作PE⊥x轴于E，表示OE和PE的长，根据点P在第二象限，可得P的坐标；
（3）根据中点坐标公式可得Q的坐标，代入抛物线的解析式可得m的值，计算对称轴，得x0的取值范围，根据两个不等式确定其解集即可．
【解析】（1）当x＝0时，y=−845×1538×（﹣3m）=3m，
∴C（0，3m），
∴OC=3m，
当y＝0时，即y=−845(x+1538)（x﹣3m）＝0，
解得：x1=−1538，x2＝3m，
∵A在B的右侧，其中m＞0，
∴A（3m，0），点B（−1538，0）；
故答案为：（−1538，0）、（3m，0）、（0，3m）；

（2）Rt△AOC中，tan∠OAC=OCOA=3m3m=33，
∴∠CAO＝30°，
∵OP2＝PC•PA，
∵∠OPC＝∠OPC，
∴△OPA∽△CPO，
∴∠POC＝∠OAC＝30°，
∵∠ACO＝∠POC+∠APO，
∴∠APO＝60°﹣30°＝30°，
∴tan∠APO=33，
过P作PE⊥x轴于E，

∵∠APO＝∠OAC＝30°，
∴PO＝OA＝3m，∠POE＝60°，
Rt△PEO中，∠EPO＝30°，
∴OE=12OP=3m2，PE=33m2，
∵点P在第二象限，
∴P（−3m2，33m2）；
（3）由（2）知：P（−3m2，33m2），
∵点Q恰好为OP的中点，
∴Q（−3m4，33m4），
∵Q在抛物线上，
则33m4=−845（−3m4+1538）（−3m4−3m），
解得：m=3，
∴抛物线的解析式为：y=−845（x+1538）（x﹣33）=−845x2+35x+3，
则对称轴是x=−352×(−845)=9316，
作抛物线的对称轴交抛物线于点F，
∵M在点C与顶点F之间（含点C与顶点F），
∴0≤x0≤9316，
∵n≤43x0+23316，
设w1＝x0+23316，
∵1＞0，
∴w1随x0的增大而增大，
∴当x0=9316时，w1有最大值，即43x0+23316有最小值为2，
∴n≤2，
对于不等式2n−916≥−4x0+3x0+138，
则n≥﹣2x02+32x0+3532=−2（x0−38）2+1916，
设w2＝﹣2（x0−38）2+1916，
∵﹣2＜0，
∴w2有最大值，
∵0＜38＜9316，
∴当x0=38时，w2有最大值为1916，
∴n≥1916，
综上，n的取值范围是1916≤n≤2．
【题组二】
5．（2020•开福区校级二模）如图，抛物线y＝mx2+4mx﹣12m（m＜0）与x轴相交于点A、B（点A在点B的右边），顶点为C．
（1）求A、B两点的坐标；
（2）若△ABC为等边三角形，点M（x0，y0）为抛物线y＝mx2+4mx﹣12m（m＜0）上任意一点，总有n−856≥1633my02+403y0﹣298成立，求n的最小值；
（3）若m=−12，点P为x轴上一动点，若α＝∠CAB+∠CPB，当tanα＝4时，求P点的坐标．

【分析】（1）令y＝mx2+4mx﹣12m＝0，解得x＝2或﹣6，即可求解；
（2）设t=1633my02+403y0﹣298，则t＝﹣4y02+403y0+2＝﹣4（y0﹣53）2﹣298≥﹣4（43−53）2+2＝﹣10，故有n−856≥−10，即可求解；
（3）证明α＝∠MCH，在△CHM中，tan∠CMH=12，tan∠MCH＝tanα＝4，利用三角形的边角关系即可求出点H的坐标，进而求解．
【解析】（1）令y＝mx2+4mx﹣12m＝0，解得x＝2或﹣6，
故点A、B的坐标分别为（2，0）、（﹣6，0）；

（2）由点AB的坐标知，AB＝8，函数的对称轴为x＝﹣2，
当x＝﹣2时，y＝mx2+4mx﹣12m＝﹣16m，
∵△ABC为等边三角形，则yC＝ACsin∠CAB＝ABsin60°＝8×32=43，
故点C的坐标为（﹣2，43），
则﹣16m＝43，解得m=−34，
则抛物线的最大值为43，即y0≤43，
设t=1633my02+403y0﹣298，
则t＝﹣4y02+403y0﹣298＝﹣4（y0﹣53）2+2≥﹣4（43−53）2+2＝﹣10，
故有n−856≥−10，解得n≥256，
故n的最小值为256；

（3）连接BC并延长交y轴于点M，设直线CP与y轴交于点H，

过点H作HK⊥CM于点K，
由点B、C的坐标得，直线BC的表达式为y＝2x+12，则点M（0，12），
则tan∠CBA＝2，则tan∠CMH=12，
由点C、M的坐标得，CM=(−2)2+(8−12)2=20，
根据函数的对称性，BC＝CA，则∠ABC＝CAB，
则α＝∠CAB+∠CPB＝∠CBA+∠CPB＝∠MCH，
在△CHM中，tan∠CMH=12，tan∠MCH＝tanα＝4，
则设HK＝4x，则CK＝x，MK＝8x，
则CM＝CK+KM＝x+8x＝9x=20，解得x=209，
HM=HK2+MK2=80x=409，
则OH＝12−409=689，故点H（0，689），
由点C、H的坐标得，直线CH的表达式为y=−29x+689，
令y＝0，则x＝34，
当点P在y轴左侧时，
同理可得，点P（﹣38，0），
故点P的坐标为（34，0）或（﹣38，0）．
6．（2020•天心区校级模拟）对某一个函数给出如下定义：若存在实数M＞0，对于任意的函数值y，都满足﹣M≤y≤M，则称这个函数是有界函数，在所有满足条件的M中，其最大值称为这个函数的边界值．例如，图中的函数是有界函数，其边界值是1．
（1）分别判断函数y=1x（x＞0）和y＝x+2（﹣4≤x≤2）是不是有界函数？若是有界函数，求其边界值；
（2）若函数y＝﹣x+2（a≤x≤b，b＞a）的边界值是3，且这个函数的最小值也是3，求b的取值范围；
（3）将函数y＝x2（﹣1≤x≤m，m≥0）的图象向下平移m个单位，得到的函数的边界值是t，当m在什么范围时，满足34≤t≤1？

【分析】（1）在x的取值范围内，y=1x（x＞0）的y无最大值，不是有界函数；y＝x+2（﹣4≤x≤2）是有界函数，其边界值是4；
（2）由一次函数的增减性，可得当x＝a时，ymax＝3，当x＝b时，y＝﹣b+2，由边界值定义可列出不等式，即可求解；
（3）先设m＞1，函数向下平移m个单位后，x＝0时，y＝﹣m＜﹣1，此时边界值t＞1，与题意不符，故m≤1，判断出函数y＝x2所过的点，结合平移，即可求解．
【解析】（1）∵y=1x（x＞0）的y无最大值，
∴y=1x不是有界函数；
∵y＝x+2（﹣4≤x≤2）是有界函数，
当x＝﹣4时，y＝﹣2，
当x＝2时，y＝4，
对于﹣4≤x≤2时，任意函数值都满足﹣4＜y≤4，
∴边界值为4；

（2）∵y＝﹣x+2，y随x的增大而减小，
∴当x＝a时，ymax＝3，当x＝b时，y＝﹣b+2，
∵边界值是3，b＞a，
∴﹣3≤﹣b+2＜3，
∴﹣1＜b≤5；

（3）若m＞1，图象向下平移m个单位后，x＝0时，y＜﹣m＜﹣1，此时函数的边界值t＞1，不合题意，故m≤1．
∴函数y＝x2（﹣1≤x≤m，m≥0），当x＝﹣1时，ymax＝1，当x＝0时，ymin＝0，
∴向下平移m个单位后，ymax＝1﹣m，ymin＝﹣m，
∵边界值34≤t≤1，
∴34≤1﹣m≤1互﹣1≤﹣m≤−34，
∴0≤m≤14或34≤m≤1．
7．（2020•长春一模）如图，在平面直角坐标系中，矩形ABCD的四个顶点坐标分别是A（﹣1，﹣1）、B（4，﹣1）、C（4，1），D（﹣1，1）．函数y=−12x2+2x−1(x≥m)x2−2mx+2m+2(x＜m)（m为常数）．
（1）当此函数的图象经过点D时，求此函数的表达式．
（2）在（1）的条件下，当﹣2≤x≤2时，求函数值y的取值范围．
（3）当此函数的图象与矩形ABCD的边有两个交点时，直接写出m的取值范围．
（4）记此函数在m﹣1≤x≤m+1范围内的纵坐标为y0，若存在1≤y0≤2时，直接写出m的取值范围．

【分析】（1）根据矩形的性质结合平面直角坐标系先确定点D的坐标，再判断出经过点D的函数，代入点D的坐标求出m的值即可；
（2）当﹣2≤x≤2时分﹣2≤x＜−12和−12≤x≤2两种情况，结合函数图象进一步确定函数的取值范围；
（3）首先确定当x＜m时，y有最小值为﹣（x﹣m）2+3，再根据m的不同取值，结合图象与矩形的边的交点个数确定m的取值范围；
（4）根据x的不同取值，分别得到关于m的不等式（组），求解不等式（组）即可．
【解析】（1）由题意得，点D的坐标为（﹣1，1），
当x＝﹣1时，y=−12−2−1=−312≠1，
∴函数y=−12x2+2x−1(x≥m)的图象不经过点D，
∴函数y＝x2﹣2mx+2m+2（x＜m）的图象经过点D，
∴（﹣1）2﹣2m×（﹣1）+2m+2＝1，
解得，m=−12，
∴y=−12x2+2x−1(x≥−12)x2+x+1(x＜−12)；
（2）由（1）可知y=−12x2+2x−1(x≥−12)x2+x+1(x＜−12)，
当﹣2≤x≤2时，分段讨论：
①当﹣2≤x＜−12时，y＝x2+x+1，
该二次函数的对称轴为直线x=−12，且开口向上，如图，

∴当﹣2≤x＜−12时，y随x的增大而减小，
当x＝﹣2时，y取最大值，最大值＝4﹣2+1＝3；
当x=−12时（取不到），y最小值=34；
所以，34＜y≤3；
②当−12≤x≤2时，y=−12x2+2x−1，
二次函数的对称轴为x＝2，开口向下，如图所示，

∴−12≤x≤2时，y随x的增大而增大，
当x=−12时，y最小值=−178，
当x＝2时，y最大值是1，
∴−178≤x≤1．
综上，当﹣2≤x＜−12时，34＜y≤3；
当−12≤x≤2时，−178≤x≤1；
∴y的取值范围是：−178≤x≤3；
（3）y1=−12x2+2x−1过点E（0，﹣1），F（2，1），B（4，﹣1）三点，
y2=x2−2mx+2m+2=（x﹣m）2﹣（m﹣1）+3恒过（1，3），对称轴为直线x＝m，
在x＜m时，y随x的增大而减小，y有最小值，最小值＝m2﹣2m2+2m+2＝﹣（m﹣1）2+3．

①若m≤0，x≥0时，则y1与矩形的边有3个交点，不符合题意；
②若0＜m≤2时，y1与矩形的边有F、B两个交点，即y2与矩形的边无交点，
∴y最小值≥1，
∴﹣（m﹣1）2+3≥1，解得，−2+1≤m≤2+1，
即：0＜m≤2；
③若2＜m≤4，x≥m时，y1与矩形的边的交点只有B，
∴y2有且只有一个交点，
∴﹣1≤﹣（m﹣1）2+3＜1，解得，﹣1≤﹣（m﹣1）2+3＜1，解得：−1≤m＜1−2或1+2＜m≤3，
∴1+2＜m≤3，
④若m＞4，y1与矩形的边无交点，则y2与矩形的边有两个交点，
即：当x＝4时，y2＜1，有两个交点，即16﹣8m+2m+2＜1，
∴m＞176，
∴m＞4，
综上，m的取值范围是：0＜m≤2或1+2＜m≤3或m＞4；
（4）①当m≤x≤m+1时，y0=y1=−12(x−2)2+1≤1，
若存在1≤y0≤2，仅有y0＝1，即x＝2时，y1＝1，
∴m≤2≤m+1，
∴1≤m≤2；
②当m﹣1≤x＜m时，y0=y2=x2−2mx+2m+2，
若存在1≤y0≤2，则−(m−1)2+3＜y2≤−(m−1)2+4，
即满足最小值小于2，最大值大于等于1即可，
∴−(m−1)2+3＜2−(m−1)2+4≥1，
∴−3+1≤m＜0或1＜m≤3+1；
综合①、②得：−3+1≤m＜0或1≤m≤3+1．
8．（2020•思明区校级模拟）已知抛物线C：y1＝a（x﹣h）2﹣1，直线l：y2＝kx﹣kh﹣1．
（1）判断命题“抛物线C的对称轴不可能是y轴”的真假，并说明理由；
（2）求证：直线l恒过抛物线C的顶点；
（3）①当a＝﹣1，m≤x≤2时，y1≥x﹣3恒成立，直接写出m的取值范围；
②当0＜a≤2，k＞0时，若在直线l下方的抛物线C上至少存在两个横坐标为整数的点，求k的取值范围．
【分析】（1）抛物线C的对称轴为x＝h，当h＝0时，抛物线C的对称轴即为y轴，即可求解；
（2）由抛物线的解析式可知抛物线的顶点坐标为（h，﹣1），然后证明点（h，﹣1）在直线y2＝kx﹣kh﹣1的解析式上即可；
（3）①令y3＝x﹣3，依据抛物线的解析式可得到抛物线的顶点在直线y＝﹣1上，由m≤x≤2时，y1≥x﹣3恒成立可得到抛物线的顶点坐标为（2，﹣1），然后找出抛物线y1＝a（x﹣2）2﹣1位于直线y3＝x﹣3上方时自变量x的取值范围，即可求解；
②由（2）可知抛物线C与直线l都过点A（h，﹣1）．当0＜a≤2时，k＞0，在直线l下方的抛物线C上至少存在两个横坐标为整数点，即当x＝h+2时，y2＞y1恒成立，然后由y2＞y1可得到关于k的不等式，进而求解．
【解析】（1）抛物线C的对称轴为x＝h，
当h＝0时，抛物线C的对称轴即为y轴，
故命题“抛物线C的对称轴不可能是y轴”为假命题；

（2）抛物线C的顶点坐标为（h，﹣1），
当x＝h 时，y2＝kh﹣kh﹣1＝﹣1，
所以直线l恒过抛物线C的顶点；

（3）①当a＝﹣1时，抛物线C解析式为y1＝﹣（x﹣h）2﹣1，
不妨令y3＝x﹣3，
如图1所示，抛物线C的顶点在直线y＝﹣1上移动，

当m≤x≤2时，y1≥x﹣3恒成立，
则可知抛物线C的顶点为（2，﹣1），
设抛物线C与直线y3＝x﹣3 除顶点外的另一交点为M，
此时点M的横坐标即为m的最小值，
由y=−(x−2)2−1y=x−3，
解得：x=1y=−2或x=2y=−1，
所以m的最小值为1，
m的取值范围为：2≥m≥1；
②如图2所示，由（2）可知：抛物线C与直线l都过点A（h，﹣1）．

当0＜a≤2时，k＞0，在直线l下方的抛物线C上至少存在两个横坐标为整数点，即当x＝h+2时，y2＞y1恒成立．
所以k（h+2）﹣kh﹣1＞a（h+2﹣h）2﹣1，整理得：k＞2a．
又因为0＜a≤2，
所以0＜2a≤4，
所以k＞4．
【题组三】
9．（2020•海陵区一模）已知抛物线y1＝ax2﹣2amx+am2+4，直线y2＝kx﹣km+4，其中a≠0，a、k、m是常数．
（1）抛物线的顶点坐标是　（m，4）　，并说明上述抛物线与直线是否经过同一点（说明理由）；
（2）若a＜0，m＝2，t≤x≤t+2，y1的最大值为4，求t的范围；
（3）抛物线的顶点为P，直线与抛物线的另一个交点为Q，对任意的m值，若1≤k≤4，线段PQ（不包括端点）上至少存在两个横坐标为整数的点，求a的范围．
【分析】（1）由抛物线y1＝ax2﹣2amx+am2+4＝a（x﹣m）2+4，可得顶点坐标，由x＝m时，可得y2＝4，即直线y2＝kx﹣km+4恒过点（m，4），即可求解；
（2）由二次函数的性质可得当x＝2时，y1有最大值4，结合t≤x≤t+2，y1的最大值为4，列出不等式组，可求解；
（3）先求出点Q的横坐标，结合“1≤k≤4，线段PQ（不包括端点）上至少存在两个横坐标为整数的点”，分两种情况，列出不等式可求解．
【解析】（1）∵y1＝ax2﹣2amx+am2+4＝a（x﹣m）2+4，
∴顶点坐标为（m，4），
∵y2＝kx﹣km+4＝k（x﹣m）+4，
当x＝m时，y2＝4，
∴直线y2＝kx﹣km+4恒过点（m，4），
∴抛物线与直线都经过同一点（m，4），
故答案为（m，4）；
（2）当m＝2时，y1＝a（x﹣2）2+4，
∵a＜0，
∴当x＝2时，y1有最大值4，
又∵t≤x≤t+2，y1的最大值为4，
∴t≤2t+2≥2，
∴0≤t≤2；
（3）令y1＝y2，则有ax2﹣2amx+am2+4＝kx﹣km+4，解得x1＝m，x2＝m+ka，
∵线段PQ上至少存在两个横坐标为整数的点，k＞0，
∴当a＞0时，m+ka−m＞2，
∴2a＜k，
又∵1≤k≤4，
∴2a＜1，即a＜12，
∴0＜a＜12；
同理当a＜0时，可求得−12＜a＜0，
综上所述：0＜a＜12或−12＜a＜0．
10．（2020•朝阳区校级一模）在平面直角坐标系中，记函数y=x2+2nx+2n2(x＜0)x2−6nx(x≥0)的图象为G，正方形ABCD的对称中心与原点重合，顶点A的坐标为（2，2），点B在第四象限．
（1）当n＝1时．
①求G的最低点的纵坐标；
②求图象G上所有到x轴的距离为2的点的横坐标之和．
（2）当图象G与正方形ABCD的边恰好有两个公共点时，直接写出n的取值范围．
【分析】（1）①画出函数图象，利用图象法解决问题即可．
②求出图象G上所有到x轴的距离为2的横坐标即可解决问题．
（2）求出经过特殊位置n的值结合图象判断即可．
【解析】（1）①y=x2+2x+2(x＜0)x2−6x(x≥0)，
函数图象如图所示：

函数最低点的坐标（3，﹣9），
∴图象G的最低点的纵坐标为﹣9．

②当y＝2时，x2+2x+2＝2，解得x＝﹣2或0（舍弃）
x2﹣6x＝2时，解得x＝3+11或3−11（舍弃），
当y＝﹣2时，x2﹣6x＝﹣2，解得x＝3+7或3−7，
∴图象G上所有到x轴的距离为2的横坐标之和＝﹣2+3+11+3+7+3−7=7+11．

（2）当y＝x2+2nx+2n2的顶点落在AD边上时，n2＝2，解得n=2或−2（舍弃）

当n=2时，y＝x2+2nx+2n2（x＜0）与边AD有一个交点，y＝x2﹣6nx与边BC有一个交点，符合题意．
当2n2≤2，解得n≤1或n≥﹣1，
当y＝x2﹣6nx经过（2，﹣2）时，n=12，
观察图象可知当12＜n≤1时，满足条件，
当y＝x2﹣6nx的顶点在BC边上时，﹣9n2＝﹣2，
解得n=23或−23（舍弃），
当n＝﹣1时，y＝x2+2nx+2n2（x＜0）与正方形的边没有交点，
观察图象可知当﹣1＜n＜23时，满足条件，
综上所述，满足条件的n的值为﹣1＜n＜23或12＜n≤1或n=2．
11．（2020•南关区校级模拟）定义：在平面直角坐标系xOy中，点P的坐标为（x，y），当x＞m时，Q点坐标为（﹣x，﹣y）；当x≤m时，Q点坐标为（﹣x，﹣y+2），则称点Q为点P的m分变换点（其中m为常数）．例如：（﹣2，3）的0分变换点坐标为（2，﹣1）．
（1）点（5，7）的1分变换点坐标为　（﹣5，﹣7）　；点（1，6）的1分变换点在反比例函数y=kx图象上，则k＝　4　；若点（a﹣1，5）的1分变换点在直线y＝x+2上，则a＝　8　
（2）若点P在二次函数y＝x2﹣2x﹣3的图象上，点Q为点P的3分变换点．
①直接写出点Q所在函数的解析式；
②求点Q所在函数的图象与直线y＝﹣5交点坐标；
③当﹣4≤x≤t时，点Q所在函数的函数值﹣5≤y≤6，直接写出t的取值范围．
（3）点A（﹣3，﹣1），B（2，﹣1），若点P在二次函数y＝x2﹣mx+m22−2的图象上，点Q为点P的m分变换点．当点Q所在的函数图象与线段AB有两个公共点时，直接写出m的取值范围．
【分析】（1）根据新定义进行解答便可；
（2）①分两种情况：x＜﹣3；x≥﹣3．根据m分变换点的定义求出Q点的坐标，进而便可写出点Q所在函数的解析式；
②把y＝﹣5代入点Q所在的函数解析式中，便可求得交点坐标；
③根据函数的性质进行解答便可；
（3）分两种情况：x＞m和x≤m求得点Q所在的函数解析式，再根据函数的性质求得函数图象与线段AB的两个公共点时的m的取值范围．
【解析】（1）∵5＞1，
∴点（5，7）的1分变换点坐标为（﹣5，﹣7）；
∵1＝1，
∴点（1，6）的1分变换点为（﹣1，﹣4），
∵点（1，6）的1分变换点在反比例函数y=kx图象上，
∴k＝﹣1×（﹣4）＝4；
当a﹣1＞1，即a＞2时，点（a﹣1，5）的1分变换点为（1﹣a，﹣5），
∵点（a﹣1，5）的1分变换点在直线y＝x+2上，
∴﹣5＝1﹣a+2，
∴a＝8，
当a﹣1≤1，即a≤2时，点（a﹣1，5）的1分变换点为（1﹣a，﹣3），
∵点（a﹣1，5）的1分变换点在直线y＝x+2上，
∴﹣3＝1﹣a+2，
∴a＝6，（不合题意舍去）
故答案为：（﹣5，﹣7）；4；8；
（2）①设Q（m，n），
∵点Q为点P的3分变换点，
∴当﹣m＞3，即m＜﹣3时，P（﹣m，﹣n），
∴﹣n＝m2+2m﹣3，
∴n＝﹣m2﹣2m+3，
∴点Q所在函数的解析式为y＝﹣x2﹣2x+3（x＜﹣3）；
当﹣m≤3，即m≥﹣3时，P（﹣m，2﹣n），
∴2﹣n＝m2+2m﹣3，
∴n＝﹣m2﹣2m+5，
∴点Q所在函数的解析式为y＝﹣x2﹣2x+5（m≥﹣3）
故点Q所在函数的解析式为y＝﹣x2﹣2x+3（x＜﹣3）或y＝﹣x2﹣2x+5（x≥﹣3）．
②把y＝﹣5代入y＝﹣x2﹣2x+3（x＜﹣3）得﹣x2﹣2x+3＝﹣5，
解得，x＝﹣4，或x＝2（舍）；
把y＝﹣5代入y＝﹣x2﹣2x+5（x≥﹣3）得，﹣x2﹣2x+5＝﹣5，
解得，x＝﹣1−11（舍弃或x＝﹣1+11，
综上，点Q所在函数的图象与直线y＝﹣5交点坐标为（﹣1+11，﹣5）或（﹣4，﹣5）．
③∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4（x＞3），
∴y的最大值为4＜6，且当x＞3时，y随x的增大而减小，
令y＝﹣5，得y＝﹣x2﹣2x+3＝﹣5（x＞3），
解得，x＝2（舍），x＝﹣4（舍）；
∵y＝﹣x2﹣2x+5＝﹣（x+1）2+6（x≤3），
∴y的最大值为6，当﹣1＜x≤3时，y随x的增大而减小，当x＜﹣1时，y随x的增大而增大，
令y＝﹣5时，得﹣x2﹣2x+5＝﹣5，
解得，x＝﹣1+11，x＝﹣1−11，
∴当﹣1≤t≤﹣1+11时，点Q所在函数的函数值﹣5≤y≤6；
综上，当﹣4≤x≤t时，点Q所在函数的函数值﹣5≤y≤6，其t的取值范围是﹣1≤t≤﹣1+11；
（3）设P（x，x2﹣mx+m22−2），则Q（﹣x，﹣x2+mx−m22+2），
∴点Q所在的函数的解析式为：y＝﹣x2﹣mx−m22+2=−(x+m2)2−m24+2，
∴顶点坐标为（−m2，−m24+2），
∵点A（﹣3，﹣1），B（2，﹣1），点Q所在的函数图象与线段AB有两个公共点，
∴−m24+2＞−1−9+3m−m22+2≤−1−4−2m−m22+2≤−1，
解得，﹣23＜m≤﹣2−2，或﹣2+2≤m＜23．
12．（2020•遵化市三模）已知点P（2，﹣3）在抛物线L：y＝ax2﹣2ax+a+k（a，k均为常数，且a≠0）上，L交y轴于点C，连接CP．
（1）用a表示k，并求L的对称轴及L与y轴的交点坐标；
（2）当L经过（3，3）时，求此时L的表达式及其顶点坐标；
（3）横、纵坐标都是整数的点叫做整点．如图，当a＜0时，若L在点C，P之间的部分与线段CP所围成的区域内（不含边界）恰有4个整点，求a的取值范围；
（4）点M（x1，y1），N（x2，y2）是L上的两点，若t≤x1≤t+1，当x2≥3时，均有y1≥y2，直接写出t的取值范围．

【分析】（1）点P（2，﹣3）代入抛物线上，则k＝﹣3﹣a；抛物线L的对称轴为直线x=−−2a2a=1，即x＝1．
（2）点（3，3），代入抛物线上，则有k＝﹣3﹣a，解得a＝2，k＝﹣5，即可求解．
（3）顶点坐标（1，﹣a﹣3），2＜﹣a﹣3≤3时在指定区域内有5个整数点．
（4）当a＞0时，t≥3或t+1≤﹣1；当a＜0时，t+1≤3或t≥﹣1．
【解析】（1）∵点P（2，﹣3）在抛物线L：y＝ax2﹣2ax+a+k（a，k均为常数且a≠0）上，
∴﹣3＝4a﹣4a+a+k，
∴k＝﹣3﹣a；
抛物线L的对称轴为直线x=−−2a2a=1，即x＝1，
与y轴的交点为（0，3）．
（2）∵L经过点（3，3），
∴9a﹣6a+a+k＝3，
∵k＝﹣3﹣a，
∴a＝2，k＝﹣5
∴L的表达式为y＝2x2﹣4x﹣3；
∵y＝2（x﹣1）2﹣5，
∴顶点坐标为（1，﹣5）；
（3）顶点坐标（1，﹣a﹣3），
∵在点C，P之间的部分与线段CP所围成的区域内（不含边界）恰有4个整点，
∴1＜﹣a﹣3≤2，
∴﹣5≤a＜﹣4；
（4）当a＞0时，t≥3或t+1≤﹣1，
∴t≥3或t≤﹣2；
观察图象，此时有不符合条件的点使y1≥y2，
故此情况舍去；
当a＜0时，t+1≤3且t≥﹣1，
∴﹣1≤t≤2；
综上所述，﹣1≤t≤2；

【题组四】
13．（2020•中原区校级模拟）如图1所示，抛物线y=23x2+bx+c与x轴交于A、B两点，与y轴交于点C，已知C点坐标为（0，4），抛物线的顶点的横坐标为72，点P是第四象限内抛物线上的动点，四边形OPAQ是平行四边形，设点P的横坐标为m．
（1）求抛物线的解析式；
（2）求使△APC的面积为整数的P点的个数；
（3）当点P在抛物线上运动时，四边形OPAQ可能是正方形吗？若可能，请求出点P的坐标，若不可能，请说明理由；
（4）在点Q随点P运动的过程中，当点Q恰好落在直线AC上时，则称点Q为“和谐点”，如图（2）所示，请直接写出当Q为“和谐点”的横坐标的值．

【分析】（1）抛物线与y轴交于点C，顶点的横坐标为72，则c=4−b2×23=72，即可求解；
（2）△APC的面积S＝S△PHA+S△PHC=12×PH×OA=12×6×（−23x+4−23x2+143x﹣4）＝﹣2x2+12（1＜x＜6），即可求解；
（3）当四边形OPAQ是正方形时，点P只能在x轴的下方，此时OAP为等腰直角三角形，设点P（x，y），则x+y＝0，即可求解；
（4）求出直线AP的表达式为：y=23（m﹣1）（x﹣6），则直线OQ的表达式为：y=23（m﹣1）x②，联立①②求出Q的坐标，又四边形OPAQ是平行四边形，则AO的中点即为PQ的中点，即可求解．
【解析】（1）抛物线与y轴交于点C，顶点的横坐标为72，则c=4−b2×23=72，解得b=−143c=4，
故抛物线的抛物线为：y=23x2−143x+4；

（2）对于y=23x2−143x+4，令y＝0，则x＝1或6，故点B、A的坐标分别为（1，0）、（6，0）；
如图，过点P作PH∥y轴交AC于点H，

由点A、C的坐标得，直线AC的表达式为：y=−23x+4①，
设点P（m，23m2−143m+4），则点H（m，−23m+4），
△APC的面积S＝S△PHA+S△PHC=12×PH×OA=12×6×（−23m+4−23m2+143m﹣4）＝﹣2m2+12m（1＜m＜6），
故在0＜S≤10时，整数的P点的个数为10个；
在10＜S＜18时，整数的P点的个数为14个；
在S＝18时，整数的P点的个数有1；
共计25个；

（3）不可能，理由：
当四边形OPAQ是正方形时，点P只能在x轴的下方，
此时，OA＝6，故点P（3，﹣3），
当x＝3时，y=23x2−143x+4≠﹣3，
故点P不在抛物线上，
故四边形OPAQ不可能是正方形；

（4）设点P（m，23m2−143m+4），而点A（6，0），
设直线AP的表达式为：y＝kx+t，
将点P、A的坐标代入上式并解得：直线AP的表达式为：y=23（m﹣1）（x﹣6），
∵AP∥OQ，则AP和OQ表达式中的k值相同，
故直线OQ的表达式为：y=23（m﹣1）x②，
联立①②并解得：x=6m，则点Q（6m，4−4m），
∵四边形OPAQ是平行四边形，则AO的中点即为PQ的中点，
则m+6m=6，解得：m＝3±3，
则6m=3±3，
故Q的横坐标的值为3±3．
14．（2020•唐山一模）如图，已知二次函数L：y＝mx2+2mx+k（其中m，k是常数，k为正整数）．
（1）若L经过点（1，k+6），求m的值．
（2）当m＝2，若L与x轴有公共点时且公共点的横坐标为非零的整数，确定k的值；
（3）在（2）的条件下将L：y＝mx2+2mx+k的图象向下平移8个单位，得到函数图象M，求M的解析式；
（4）将M的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象N，请结合新的图象解答问题，若直线y=12x+b与N有两个公共点时，请直接写出b的取值范围．

【分析】（1）将点（1，k+6）代入y＝mx2+2mx+k，即可求解；
（2）由题意得：△＝16﹣8k≥0，即可求解；
（3）根据平移的公式即可求解；
（4）确定点H、A、B三个临界点，求出临界点时b的值，即可求解．
【解析】（1）将点（1，k+6）代入y＝mx2+2mx+k并解得：
m＝2；

（2）y＝mx2+2mx+k＝2x2+4x+k，
由题意得：△＝16﹣8k≥0，解得：k≤2，
∵k为正整数，当k＝1时，方程没有整数解，故舍去，
则k＝2；

（3）在m＝2，k＝2时，y＝2x2+4x+2，向下平移8个单位，
平移后的表达式为：y＝2x2+4x+2﹣8＝2x2+4x﹣6；

（4）由（3）知，M的表达式为：y＝2x2+4x﹣6①，
则翻折后抛物线的表达式为：y′＝﹣2x2﹣4x+6②，
设直线m为：y=12x+b③，
①当直线m与翻折后的图象有一个交点（点H）时，如下图，

联立②③并整理得：2x2+92x+b﹣6＝0，
则△=814−8（b﹣6）＝0，解得：b=27332；
②当直线m过点A（﹣3，0）时，
将点A的坐标代入③式得，0=12×（﹣3）+b，解得：b=32；
③当直线m过点B时，
同理可得：b=−12；
故直线y=12x+b与N有两个公共点时，b的取值范围为：−12＜b＜32或b＞27332．
15．（2020•平谷区二模）在平面直角坐标系xOy中，抛物线y＝mx2﹣2mx﹣1（m＞0）与x轴的交点为A，B，与y轴交点C．
（1）求抛物线的对称轴和点C坐标；
（2）横、纵坐标都是整数的点叫做整点．抛物线在点A，B之间的部分与线段AB所围成的区域为图形W（不含边界）．
①当m＝1时，求图形W内的整点个数；
②若图形W内有2个整数点，求m的取值范围．

【分析】（1）直接利用对称轴公式计算，即可得出抛物线的对称轴，再令x＝0，即可求出点C的坐标；
（2）①先确定出抛物线解析式，即可得出结论；
②先判断出满足条件的整数点由（1，﹣1），进而抛物线的顶点坐标的范围即可得出结论．
【解析】（1）∵抛物线的解析式为y＝mx2﹣2mx﹣1（m＞0），
∴抛物线的对称轴为直线x=−−2m2m=1，
令x＝0，则y＝﹣1，
∴C（0，﹣1）；

（2）①当m＝1时，抛物线的解析式为y＝x2﹣2x﹣1，
由（1）知，C（0，﹣1），抛物线的对称轴为直线x＝1，
∴抛物线还经过（2，﹣1），
∵抛物线的顶点坐标为（1，﹣2），
∴图形W内的整点只有（1，﹣1）一个；

②如图，
由①知，抛物线过点（0，﹣1），（2，﹣1），
∵图形W内有2个整数点，
∴﹣3≤4m×(−1)−(2m)24m＜−2，
∴1＜m≤2．

16．（2020•越秀区校级一模）已知抛物线y＝x2﹣bx+c（b，c为常数，b＞0）经过点A（﹣1，0），点M（m，0）是x轴正半轴上的动点．
（1）当b＝2时，求抛物线的顶点坐标；
（2）点D（b，yD）在抛物线上，当AM＝AD，m＝3时，求b的值；
（3）点Q（b+12，yQ）在抛物线上，当6AM+23QM的最小值为4564时，求b的值．（说明：yD表示D点的纵坐标，yQ表示Q点的纵坐标）
【分析】（1）将点A（﹣1，0）代入y＝x2﹣bx+c，求出c关于b的代数式，再将b代入即可求出c的值，可进一步写出抛物线解析式及顶点坐标；
（2）将点D（b，yD）代入抛物线y＝x2﹣bx﹣b﹣1，求出点D纵坐标为﹣b﹣1，由b＞0判断出点D（b，﹣b﹣1）在第四象限，且在抛物线对称轴x=b2的右侧，过点D作DE⊥x轴，可证△ADE为等腰直角三角形，利用锐角三角函数可求出b的值；
（3）将点Q（b+12，yQ）代入抛物线y＝x2﹣bx﹣b﹣1，求出Q纵坐标为−b2−34，可知点Q（b+12，−b2−34）在第四象限，且在直线x＝b的右侧，点N（0，1），过点Q作直线AN的垂线，垂足为G，QG与x轴相交于点M，过点Q作QH⊥x轴于点H，则点H（b+12，0），在Rt△MQH中，可知∠QMH＝∠MQH＝45°，设点M（m，0），则可用含b的代数式表示m，因为6AM+23QM=4564，可得方程6[（b2−14）﹣（﹣1）]+23•2[（b+12）﹣（b2−14）]=4564，即可求解．
【解析】（1）∵抛物线y＝x2﹣bx+c经过点A（﹣1，0），
∴1+b+c＝0，
即c＝﹣b﹣1，
当b＝2时，
y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线的顶点坐标为（1，﹣4）；
（2）由（1）知，抛物线的解析式为y＝x2﹣bx﹣b﹣1，
∵点D（b，yD）在抛物线y＝x2﹣bx﹣b﹣1上，
∴yD＝b2﹣b•b﹣b﹣1＝﹣b﹣1，
由b＞0，得b＞b2＞0，﹣b﹣1＜0，
∴点D（b，﹣b﹣1）在第四象限，且在抛物线对称轴x=b2的右侧，
如图1，过点D作DE⊥x轴，垂足为E，则点E（b，0），

∴AE＝b+1，DE＝b+1，得AE＝DE，
∴在Rt△ADE中，∠ADE＝∠DAE＝45°，
∴AD=2AE，
由已知AM＝AD，m＝3，
∴3﹣（﹣1）=2（b+1），
∴b＝22−1；
（3）∵点Q（b+12，yQ）在抛物线y＝x2﹣bx﹣b﹣1上，
∴yQ＝（b+12）2﹣b（b+12）﹣b﹣1=−b2−34，
可知点Q（b+12，−b2−34）在第四象限，且在直线x＝b的右侧，
∵6AM+23QM＝23（22AM+QM），
∴可取点N（0，1），
如图2，过点Q作直线AN的垂线，垂足为G，QG与x轴相交于点M，

由∠GAM＝45°，得22AM＝GM，
则此时点M满足题意，
过点Q作QH⊥x轴于点H，则点H（b+12，0），
在Rt△MQH中，可知∠QMH＝∠MQH＝45°，
∴QH＝MH，QM=2MH，
∵点M（m，0），
∴0﹣（−b2−34）＝（b+12）﹣m，
解得，m=b2−14，
∵6AM+23QM=4564，
∴6[（b2−14）﹣（﹣1）]+23•2[（b+12）﹣（b2−14）]=4564，
∴b＝6．
【题组五】
17．（2020•丰台区二模）在平面直角坐标系xOy中，抛物线y＝ax2﹣4ax+3a与y轴交于点A．
（1）求点A的坐标（用含a的式子表示）；
（2）求抛物线与x轴的交点坐标；
（3）已知点P（a，0），Q（0，a﹣2），如果抛物线与线段PQ恰有一个公共点，结合函数图象，求a的取值范围．
【分析】（1）根据抛物线y＝ax2﹣4ax+3a与y轴交于点A即可直接写出点A的坐标；
（2）解方程即可得到结论；
（3）根据点P（a，0），Q（0，a﹣2），如果抛物线与线段PQ恰有一个公共点，结合函数图象，即可求a的取值范围．
【解析】（1）∵抛物线y＝ax2﹣4ax+3a与y轴交于点A，
∴A的坐标为（0，3a）；
（2）当y＝0时．即ax2﹣4ax+3a＝0，
解得：x1＝1，x2＝3，
∴抛物线与x轴的交点坐标为（1，0），（3，0）；
（3）当抛物线过点Q（0，a﹣2）时，a＝﹣1，

∴P（﹣1，0），
此时，抛物线与线段PQ有一个公共点．
当抛物线过点P（a，0）时，a＝1或a＝3（不合题意舍去），

此时，Q（0，﹣1），抛物线与线段PQ有一个公共点；
综上所述，当﹣1≤a＜0或1≤a＜3时，抛物线与线段PQ恰有一个公共点．
18．（2020•密云区二模）在平面直角坐标系xOy中，抛物线C1：y＝x2+bx+c与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．点B的坐标为（3，0），将直线y＝kx沿y轴向上平移3个单位长度后，恰好经过B、C两点．
（1）求k的值和点C的坐标；
（2）求抛物线C1的表达式及顶点D的坐标；
（3）已知点E是点D关于原点的对称点，若抛物线C2：y＝ax2﹣2（a≠0）与线段AE恰有一个公共点，结合函数的图象，求a的取值范围．

【分析】（1）先求出平移后解析式，将点B坐标代入可求k的值，即可求直线解析式，可得点C坐标；
（2）将点B，点C坐标代入解析式可求抛物线解析式，即可求点D坐标；
（3）利用函数图象列出不等式组，即可求解．
【解析】（1）∵将直线y＝kx沿y轴向上平移3个单位长度，
∴平移后直线解析式为：y＝kx+3，
∵直线y＝kx+3经过点B（3，0），
∴3k+3＝0，
∴k＝﹣1，
∴平移后解析式为：y＝x+3，
∵y＝﹣x+3与y轴的交点为C，
∴y＝0+3＝3，
∴点C（0，3）；
（2）∵抛物线y＝x2+bx+c经过点B（3，0）和点C（0，3），
∴c=30=9+3b+c，
解得b=−4c=3，
∴抛物线C1的函数表达式为y＝x2﹣4x+3，
∵y＝x2﹣4x+3＝（x﹣2）2﹣1，
∴顶点D的坐标为（2，﹣1）；

（3）∵抛物线C1：y＝x2﹣4x+3与x轴交于A、B两点，
∴点A（1，0），点B（3，0），
∵点E是点D关于原点的对称点，
∴点E的坐标为（﹣2，1），
如图，

由图象可得：a×1−2＜0a×(−2)2−2≥1，
∴a的取值范围是34≤a＜2．
19．（2020•北京二模）在平面直角坐标系xOy中，抛物线y＝ax2﹣4ax（a≠0）与x轴交于点A，B（A在B的左侧）．
（1）求点A，B的坐标及抛物线的对称轴；
（2）已知点P（2，2），Q（2+2a，5a），若抛物线与线段PQ有公共点，请结合函数图象，求a的取值范围．

【分析】（1）令y＝0，求出x的值，可求出A，B两点的坐标，由对称性可得出抛物线的对称轴方程；
（2）①当a＞0时，抛物线开口向上，顶点位于x轴下方，且Q（2+2a，5a）位于点P的右侧，②当a＜0时，抛物线开口向下，顶点位于x轴上方，点Q（2+2a，5a）位于点P的左侧，分别画出函数的图象，由图象可得出答案．
【解析】（1）∵y＝ax2﹣4ax＝ax（x﹣4），
∴y＝0时，ax（x﹣4）＝0，
∴x＝0或x＝4，
∴抛物线与x轴交于点A（0，0），B（4，0）．
∴抛物线y＝ax2﹣4ax的对称轴为直线：x=−−4a2a=2．
（2）y＝ax2﹣4ax＝a（x2﹣4x）＝a（x﹣2）2﹣4a，
∴抛物线的顶点坐标为（2，﹣4a）．
令y＝5a，得ax2﹣4ax＝5a，a（x﹣5）（x+1）＝0，
解得x＝﹣1或x＝5，
∴当y＝5a时，抛物线上两点M（﹣1，5a），N（5，5a）．
①当a＞0时，抛物线开口向上，顶点位于x轴下方，且Q（2+2a，5a）位于点P的右侧，
如图1，当点N位于点Q左侧时，抛物线与线段PQ有公共点，

此时2+2a≥5，
解得a≥32．
②当a＜0时，抛物线开口向下，顶点位于x轴上方，点Q（2+2a，5a）位于点P的左侧，
（ⅰ）如图2，当顶点位于点P下方时，抛物线与线段PQ有公共点，

此时﹣4a≤2，
解得a≥−12．
（ⅱ）如图3，当顶点位于点P上方，点M位于点Q右侧时，抛物线与线段PQ有公共点，

此时2+2a≤﹣1，
解得a≤−32．
综上，a的取值范围是a≥32或−12≤a＜0或a≤−32．
20．（2020•西城区二模）在平面直角坐标系xOy中，抛物线y＝x2+bx+c与x轴交于点A，B（A在B的左侧），抛物线的对称轴与x轴交于点D，且OB＝2OD．
（1）当b＝2时，
①写出抛物线的对称轴；
②求抛物线的表达式；
（2）存在垂直于x轴的直线分别与直线l：y＝x+b+22和拋物线交于点P，Q，且点P，Q均在x轴下方，结合函数图象，求b的取值范围．
【分析】（1）①由二次函数的对称轴方程可得出答案；
②根据题意求出B点坐标为（2，0），代入抛物线解析式y＝x2+2x+c可得出答案；
（2）求出E（−b+22，0），点D的坐标为（−b2，0）．①当b＞0时，得出点A的坐标为（﹣2b，0），点B的坐标为（b，0），则﹣2b＜−b+22，解不等式即可；②当b＜0时，点A的坐标为（0，0），点B的坐标为（﹣b，0），则0＜−b+22，解出b＜﹣2．
【解析】（1）当b＝2时，抛物线y＝x2+bx+c化为y＝x2+2x+c．
①抛物线的对称轴x=−b2a=−22×1=−1．
②∵抛物线的对称轴为直线x＝﹣1，
∴点D的坐标为（﹣1，0），OD＝1．
∵OB＝2OD，
∴OB＝2．
∵点A，点B关于直线x＝﹣1对称，
∴点B在点D的右侧．
∴点B的坐标为（2，0）．
∵抛物线y＝x2+2x+c与x轴交于点B（2，0），
∴4+4+c＝0．
解得c＝﹣8．
∴抛物线的表达式为y＝x2+2x﹣8．
（2）设直线y＝x+b+22与x轴交点为点E，
∵y＝0时，x=−b+22，
∴E（−b+22，0）．
∵抛物线的对称轴为x=−b2，
∴点D的坐标为（−b2，0），
①当b＞0时，OD=b2，
∵OB＝2OD，
∴OB＝b．
∴点A的坐标为（﹣2b，0），点B的坐标为（b，0）．

如图1，当﹣2b＜−b+22时，存在垂直于x轴的直线分别与直线l：y＝x+b+22和抛物线交于点P，Q，且点P，Q均在x轴下方，
解得b＞23．
②当b＜0时，﹣b＞0．
∴OD=−b2，
∵OB＝2OD，
∴OB＝﹣b．
∵抛物线y＝x2+bx+c与x轴交于点A，B，且A在B的左侧，
∴点A的坐标为（0，0），点B的坐标为（﹣b，0）．

如图2，当0＜−b+22时，存在垂直于x轴的直线分别与直线l：y＝x+b+22和抛物线交于点P，Q，且点P，Q均在x轴下方，
解得b＜﹣2．
综合以上可得，b的取值范围是b＜﹣2或b＞23．
【题组六】
21．（2020•顺义区二模）在平面直角坐标系xOy中，已知抛物线y＝mx2﹣3（m﹣1）x+2m﹣1（m≠0）．
（1）当m＝3时，求抛物线的顶点坐标；
（2）已知点A（1，2）．试说明抛物线总经过点A；
（3）已知点B（0，2），将点B向右平移3个单位长度，得到点C，若抛物线与线段BC只有一个公共点，求m的取值范围．
【分析】（1）求出抛物线的解析式，由配方法可得出答案；
（2）把x＝1，y＝2代入y＝mx2﹣3（m﹣1）x+2m﹣1，可得出答案；
（3）分三种情况：①当抛物线的顶点是点A（1，2）时，抛物线与线段BC只有一个公共点，求出m＝3；
②当抛物线过点B（0，2）时，将点B（0，2）代入抛物线表达式，得2m﹣1＝2．解得m=32，则当0＜m＜32时，抛物线与线段BC只有一个公共点．
③当抛物线过点C（3，2）时，将点C（3，2）代入抛物线表达式，得m＝﹣3＜0．则当﹣3＜m＜0时，抛物线与线段BC只有一个公共点．
【解析】（1）把m＝3代入y＝mx2﹣3（m﹣1）x+2m﹣1中，得y＝3x2﹣6x+5＝3（x﹣1）2+2，
∴抛物线的顶点坐标是（1，2）．
（2）当x＝1时，y＝m﹣3（m﹣1）+2m﹣1＝m﹣3m+3+2m﹣1＝2．
∵点A（1，2），
∴抛物线总经过点A．
（3）∵点B（0，2），由平移得C（3，2）．
①当抛物线的顶点是点A（1，2）时，抛物线与线段BC只有一个公共点．
由（1）知，此时，m＝3．
②当抛物线过点B（0，2）时，
将点B（0，2）代入抛物线表达式，得
2m﹣1＝2．
∴m=32＞0．
此时抛物线开口向上（如图1）．

∴当0＜m＜32时，抛物线与线段BC只有一个公共点．
③当抛物线过点C（3，2）时，
将点C（3，2）代入抛物线表达式，得
9m﹣9（m﹣1）+2m﹣1＝2．
∴m＝﹣3＜0．
此时抛物线开口向下（如图2）．

∴当﹣3＜m＜0时，抛物线与线段BC只有一个公共点．
综上，m的取值范围是m＝3或0＜m＜32或﹣3＜m＜0．
22．（2020•惠安县校级模拟）已知抛物线C：y＝ax2+bx+c（a＞0）的顶点在第一象限，且与直线y＝1只有一个公共点．
（1）若抛物线的对称轴为直线x＝1，求a、c之间应当满足的关系式；
（2）若b＝﹣2，点P是抛物线的顶点，且点P与点Q关于y轴对称，△OPQ是等腰直角三角形．
①求抛物线的解析式；
②直线y＝kx（k＞0）与抛物线C1交于两不同点A、B（点A在点B的左侧），与直线y＝﹣2x+4交于点R．求证：对于每个给定的实数k，总有1OA+1OB=2OR成立．
【分析】（1）抛物线顶点坐标为（1，1），当x＝1时，y＝a+b+c＝1，而x=−b2a=1，即可求解；
（2）①PQ＝2t，OP=t2+1=OQ，△OPQ是等腰直角三角形，则OP2+OQ2＝PQ2，即可求解；②求出点A、B、R的横坐标，即可求解．
【解析】（1）抛物线与直线y＝1只有一个公共点，则抛物线顶点的纵坐标为1，
而抛物线的对称轴为直线x＝1，故顶点坐标为（1，1），
当x＝1时，y＝a+b+c＝1，
而x=−b2a=1，即b＝﹣2a，
故﹣a+c＝1，
故a＝c﹣1；

（2）①b＝﹣2，则抛物线的表达式为：y＝ax2﹣2x+c，
设点P（t，1），则点Q（﹣t，1），
则PQ＝2t，OP=t2+1=OQ，
∵△OPQ是等腰直角三角形，
∴OP2+OQ2＝PQ2，即2（t2+1）＝4t2，
解得：t＝±1（舍去﹣1），
故点P（1，1），
由（1）得，b＝﹣2a＝﹣2，解得：a＝1，c＝a+1＝2，
故抛物线的表达式为：y＝x2﹣2x+2；

②如图，过点A、R、B分别作x轴的垂线，垂足分别为M、H、N，

则OAOM=OBON=OROH，
设OAOM=OBON=OROH=1m（m＞0，m为常数），
则OM＝m•AO，ON＝m•OB，OH＝m•OR
∵点A、B是直线y＝kx与抛物线的交点，
∴联立两个函数表达式并整理得：x2﹣（2+k）x+2＝0，
故x1+x2＝2+k，x1•x2＝2，
故1x1+1x2=x1+x2x1x2=2+k2，
∴1OM+1ON=2+k2，即1m⋅OA+1m⋅OB=2+k2，
联立两条直线表达式得y=kxy=−2x+4，解得：x=4k+2=OH＝m•OR，
∴1m⋅OR=k+24=12（1m⋅OA+1m⋅OB），
故每个给定的实数k，总有1OA+1OB=2OR成立．
23．（2020•河北区一模）在平面直角坐标系中，抛物线y＝ax2﹣3ax﹣1与x轴交于A、B两点（点A在点B的右侧）与y轴交于点C．
（Ⅰ）当点（1，−32）在二次函数y＝ax2﹣3ax﹣1上时．
（i）求二次函数解析式；
（ii）P为第四象限内的抛物线上的一动点，连接PA、PC．若△PAC的面积最大时，求点P的坐标；
（Ⅱ）点M、N的坐标分别为（1，2），（4，2），连接MN，直接写出线段MN与二次函数y＝ax2﹣3ax﹣1的图象只有一个交点时a的取值范围．
【分析】（Ⅰ）（i）当点（1，−32）在二次函数y＝ax2﹣3ax﹣1上时，故−32=a﹣3a﹣1，解得：a=14，即可求解；（ii）△PAC的面积S=12×PF×（OE+EA）=12×（−14m2+m）×AO=−12m2+2m=−12（m﹣2）2+2，即可求解；
（Ⅱ）分a＞0、a＜0两种情况，结合函数图象即可求解．
【解析】（Ⅰ）（i）当点（1，−32）在二次函数y＝ax2﹣3ax﹣1上时，
故−32=a﹣3a﹣1，解得：a=14；
故二次函数解析式为：y=14x2−34x﹣1；
（ii）对于y=14x2−34x﹣1，令x＝0，y＝﹣1，令y＝0，x＝4或﹣1，
故点A、B、C的坐标分别为：（4，0）、（﹣1，0）、（0，﹣1），
设直线AC的表达式为：y＝kx+b，则4k+b=0b=−1，解得：k=14b=−1，
故直线AC的表达式为：y=14x﹣1，
过点P作PE⊥x轴于点E，交AC于点F，

设点P（m，14m2−34m﹣1），则点F（m，14m﹣1），
则PF＝（14m﹣1）﹣（14m2−34m﹣1）=−14m2+m，
△PAC的面积S=12×PF×（OE+EA）=12×（−14m2+m）×AO=−12m2+2m=−12（m﹣2）2+2，
∵当m＝2时，S有最大值，此时点P（2，−32）；

（Ⅱ）当a＞0时，如图2，

函数的对称轴为x=−b2a=32，
线段与抛物线有一个交点只能如图所示，临界点为点N，
当抛物线过点N时，x＝4，y＝ax2﹣3ax﹣1＝4a﹣1＝2，解得：a=34，
故线段MN与二次函数y＝ax2﹣3ax﹣1的图象只有一个交点时a≥34；
当a＜0时，分两种情况，
当抛物线顶点过MN时，即x=32时，y＝ax2﹣3ax﹣1=94a−92a﹣1＝2，解得：a=−43；
当抛物线顶点不过MN时，如图3所示，

同理可得，临界点为点M，故当x＝1时，y＝ax2﹣3ax﹣1＝a﹣3a﹣1＝2，解得：a=−32，
故a＜−32；
综上，a≥34或a=−43或a＜−32．
24．（2020•永康市一模）我们知道求函数图象的交点坐标，可以联立两个函数解析式组成方程组，方程组的解就是交点的坐标．如：求直线y＝2x+3与y＝﹣x+6的交点坐标，我们可以联立两个解析式得到方程组y=2x+3y=−x+6，解得x=1y=5，所以直线y＝2x+3与y＝﹣x+6的交点坐标为（1，5）．请利用上述知识解决下列问题：
（1）已知直线y＝kx﹣2和抛物线y＝x2﹣2x+3，
①当k＝4时，求直线与抛物线的交点坐标；
②当k为何值时，直线与抛物线只有一个交点？
（2）已知点A（a，0）是x轴上的动点，B（0，42），以AB为边在AB右侧做正方形ABCD，当正方形ABCD的边与反比例函数y=22x的图象有4个交点时，试求a的取值范围．

【分析】（1）①由题意得：y=4x−2y=x2−2x+3，解得x1=1y1=2，x2=5y2=18，即可求解；②利用△＝0，即可求解；
（2）分a＞0、a＜0两种情况，探讨正方形的边与反比例函数图象交点的情况，进而求解．
【解析】（1）①由题意得：y=4x−2y=x2−2x+3，解得：x1=1y1=2，x2=5y2=18，
所以直线与抛物线的交点坐标是（1，2），（5，18）；
②联立两个函数并整理得：x2﹣（k+2）x+5＝0，
△＝（﹣k﹣2）2﹣4×5＝0，
解得：k＝﹣2±25；

（2）①当a＞0时，如图1，

点A、B的坐标分别为：（a，0）、（0，42），
由点A、B的坐标得，直线AB的表达式为：y=−42ax+42，
当线段AB与双曲线有一个交点时，
联立AB表达式与反比例函数表达式得：−42ax+42=22x，
整理得：4x2﹣4ax+2a＝0，
△＝（﹣4a）2﹣16×2a＝0，解得：a＝2，
故当a＞2时，正方形ABCD与反比例函数的图象有4个交点；
②当a＜0时，如图2，

（Ⅰ）当边AD与双曲线有一个交点时，
过点D作ED⊥x轴于点E，
∵∠BAO+∠DAE＝90°，∠DAE+∠ADE＝90°，
∴∠ADE＝∠BAO，
∵AB＝AD，∠AOB＝∠DEA＝90°，
∴△AOB≌△DEA（AAS），
∴ED＝AO＝﹣a，AE＝OB＝42，
故点D（a+42，a），
由点A、D的坐标可得，直线AD的表达式为：y=28a（x﹣a），
联立AD与反比例函数表达式并整理得：ax2﹣a2x﹣16＝0，
△＝（﹣a2）2﹣4a×（16）＝0，解得：a＝﹣4（不合题意值已舍去）；
（Ⅱ）当边BC与双曲线有一个交点时，
同理可得：a＝﹣16，
所以当正方形ABCD的边与反比例函数的图象有4个交点时，a的取值范围为：﹣16＜a＜﹣4；
综上所述，a的取值范围是a＞2或﹣16＜a＜﹣4．