数学八年级上册本节综合优秀同步训练题

这是一份数学八年级上册本节综合优秀同步训练题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(12×3=36分)
1. 将一副三角板按图中方式叠放，则∠α等于( )

A. 90°B. 75°C. 60°D. 45°
2. 若∆ABC三个内角的关系为∠A3=∠B4=∠C5，则三角形的形状为( )
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形
3. 如图，在△ABC中，∠ACB=100°，∠A=20°，D是AB上一点，将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于( )
A. 20°B. 40°C. 55°D. 30
4. 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于( )
A．40°B．45° C．50°D．55°
5. 如图，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为( ）
A．65°B．35°C．55°D．45°
6. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=30，∠2=20°，则∠B=( ）
A. 20°B. 30°C. 40°D. 50°
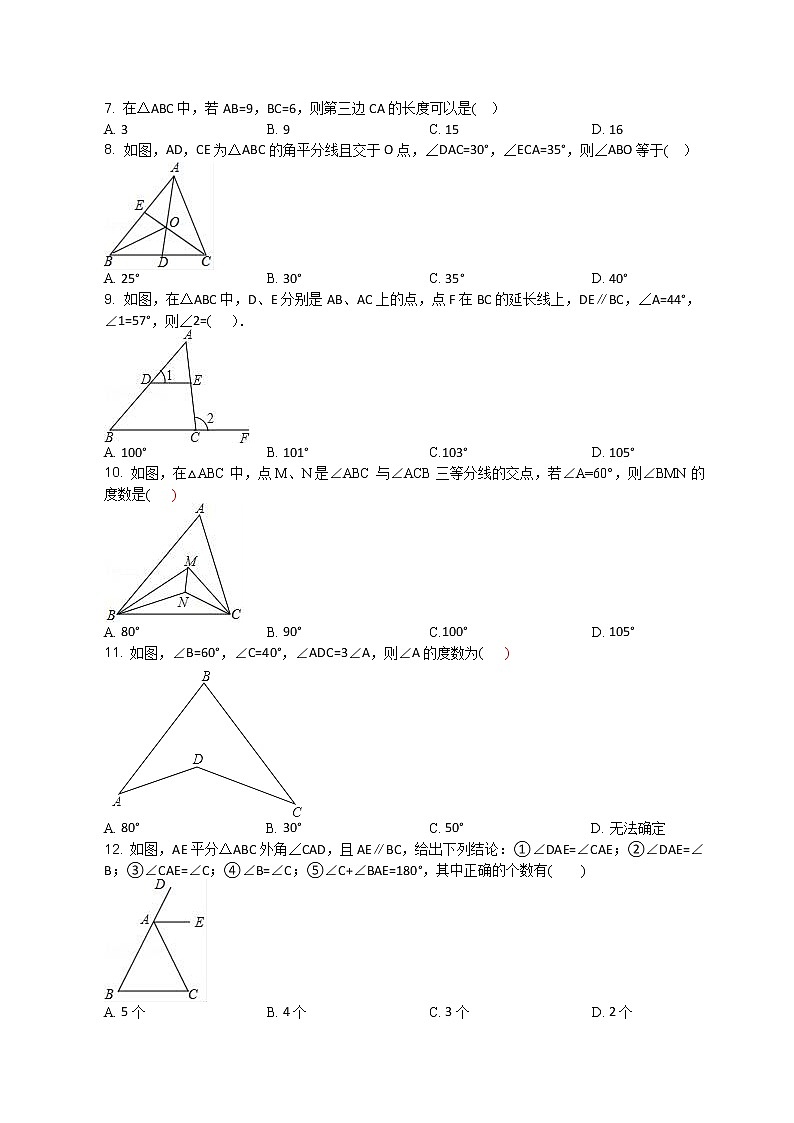
7. 在△ABC中，若AB=9，BC=6，则第三边CA的长度可以是( ）
A. 3B. 9C. 15D. 16
8. 如图，AD，CE为△ABC的角平分线且交于O点，∠DAC=30°，∠ECA=35°，则∠ABO等于( ）
A. 25°B. 30°C. 35°D. 40°
9. 如图，在△ABC中，D、E分别是AB、AC上的点，点F在BC的延长线上，DE∥BC，∠A=44°，∠1=57°，则∠2=( ）．
A. 100°B. 101°C.103°D. 105°
10. 如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点，若∠A=60°，则∠BMN的度数是( )
A. 80°B. 90°C.100°D. 105°
11. 如图，∠B=60°，∠C=40°，∠ADC=3∠A，则∠A的度数为( )
A. 80°B. 30°C. 50°D. 无法确定
12. 如图，AE平分△ABC外角∠CAD，且AE∥BC，给出下列结论：①∠DAE=∠CAE；②∠DAE=∠B；③∠CAE=∠C；④∠B=∠C；⑤∠C+∠BAE=180°，其中正确的个数有( )
A. 5个B. 4个C. 3个D. 2个
二、填空题(5×3=15分)
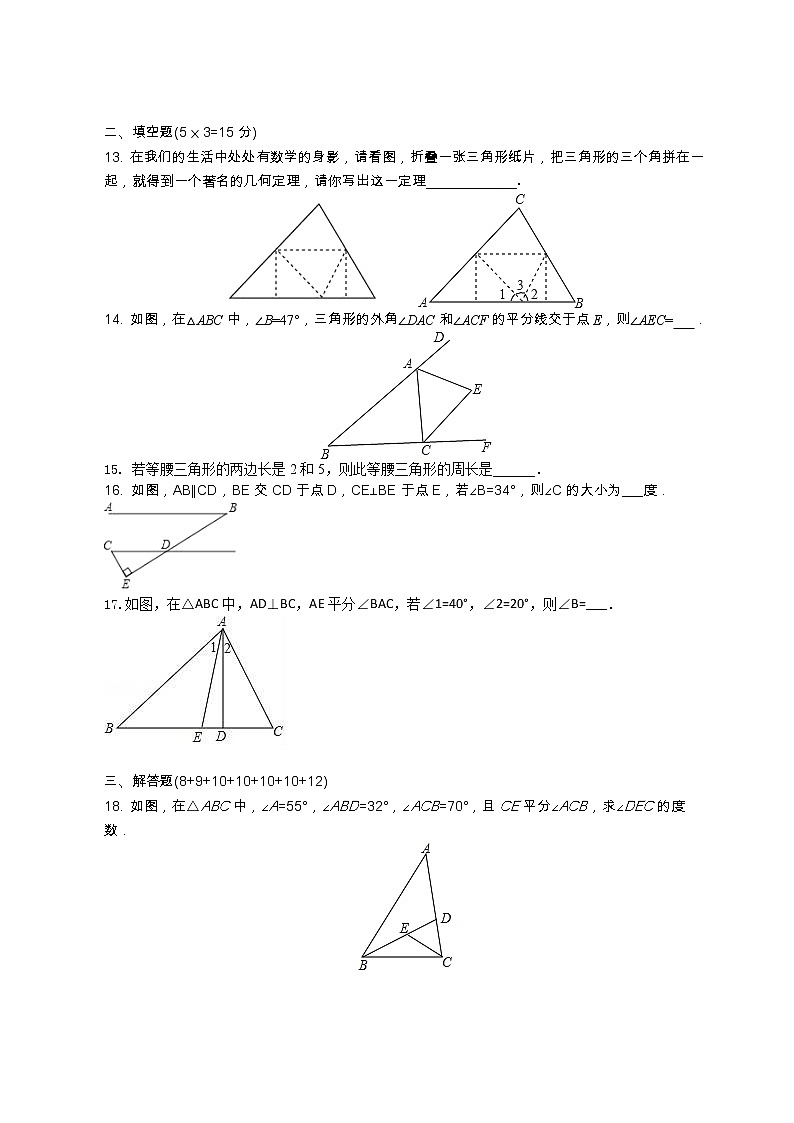
13. 在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸片，把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写出这一定理__ __．

14. 如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC= ．
15. 若等腰三角形的两边长是2和5，则此等腰三角形的周长是______．
16. 如图，AB∥CD，BE交CD于点D，CE⊥BE于点E，若∠B=34°，则∠C的大小为___度．
17.如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=40°，∠2=20°，则∠B=___．
三、解答题(8+9+10+10+10+10+12)
18. 如图，在△ABC中，∠A=55°，∠ABD=32°，∠ACB=70°，且CE平分∠ACB，求∠DEC的度数．
19. 如图，把△ABC沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是什么？试说明你找出的规律的正确性．
20. 如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC的平分线，∠A =58°，求∠H的度数．
21. （1）如图①所示，∠1+∠2与∠B+∠C有什么关系？为什么？
（2）如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时，则∠A与∠α+∠β之间有一种数量关系始终保持不变，请写出这个规律并说明理由．
22. 如图，在△ABC中，BD⊥AC于D．若∠A：∠ABC：∠ACB=3：4：5，E为线段BD上任一点．
（1）试求∠ABD的度数；
（2）求证：∠BEC＞∠A．
23. 如图，△ABC中，∠A=100∘， = 1 \* GB2 ⑴BI、CI分别平分∠ABC，∠ACB，求∠BIC的度数？ = 2 \* GB2 ⑵若BM、CM分别平分∠ABC，∠ACB的外角平分线，求∠M的度数？
24. 如图，在△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，且CF∥AD．
（1）如图1，若△ABC是锐角三角形，∠B=30°，∠ACB=70°，则∠CFE= 度；
（2）若图1中的∠B=x，∠ACB=y，则∠CFE= ；（用含x、y的代数式表示）
（3）如图2，若△ABC是钝角三角形，其他条件不变，则（2）中的结论还成立吗？请说明理由．
答案
一、选择题(12×3=36分)
1. 将一副三角板按图中方式叠放，则∠α等于( B )

A. 90°B. 75°C. 60°D. 45°
2. 若∆ABC三个内角的关系为∠A3=∠B4=∠C5，则三角形的形状为( A )
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形
3. 如图，在△ABC中，∠ACB=100°，∠A=20°，D是AB上一点，将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于( B )
A. 20°B. 40°C. 55°D. 30
4. 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于( C )
A．40°B．45° C．50°D．55°
5. 如图，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为( B）
A．65°B．35°C．55°D．45°
6. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=30，∠2=20°，则∠B=( D）
A. 20°B. 30°C. 40°D. 50°
7. 在△ABC中，若AB=9，BC=6，则第三边CA的长度可以是( B）
A. 3B. 9C. 15D. 16
8. 如图，AD，CE为△ABC的角平分线且交于O点，∠DAC=30°，∠ECA=35°，则∠ABO等于( A）
A. 25°B. 30°C. 35°D. 40°
9. 如图，在△ABC中，D、E分别是AB、AC上的点，点F在BC的延长线上，DE∥BC，∠A=44°，∠1=57°，则∠2=( B）．
A. 100°B. 101°C.103°D. 105°
10. 如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点，若∠A=60°，则∠BMN的度数是( C)
A. 80°B. 90°C.100°D. 105°
11. 如图，∠B=60°，∠C=40°，∠ADC=3∠A，则∠A的度数为( C)
A. 80°B. 30°C. 50°D. 无法确定
12. 如图，AE平分△ABC外角∠CAD，且AE∥BC，给出下列结论：①∠DAE=∠CAE；②∠DAE=∠B；③∠CAE=∠C；④∠B=∠C；⑤∠C+∠BAE=180°，其中正确的个数有( A )
A. 5个B. 4个C. 3个D. 2个
二、填空题(5×3=15分)
13. 在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸片，把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写出这一定理___三角形的内角和是180°__．

14. 如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC= 66.5° ．
15. 若等腰三角形的两边长是2和5，则此等腰三角形的周长是___12____．
16. 如图，AB∥CD，BE交CD于点D，CE⊥BE于点E，若∠B=34°，则∠C的大小为__56 _度．
17.如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=40°，∠2=20°，则∠B=__30° __．
三、解答题(8+9+10+10+10+10+12)
18. 如图，在△ABC中，∠A=55°，∠ABD=32°，∠ACB=70°，且CE平分∠ACB，求∠DEC的度数．
解：在△ABC中，∵∠A=55°，∠ACB=70°，
∴∠ABC=55°，
∵∠ABD=32°，
∴∠CBD=∠ABC–∠ABD=23°，
∵CE平分∠ACB，
∴∠BCE=12∠ACB=35°，
∴在△BCE中，∠DEC=∠CBD+∠BCE=58°．
19. 如图，把△ABC沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是什么？试说明你找出的规律的正确性．
解：2∠A=∠1+∠2，
理由是：延长BD和CE交于A′，
∵把△ABC沿DE折叠，当点A落在四边形BCDE内部，
∴∠ADE=∠A′DE，∠AED=∠A′ED，
∴2∠ADE=180°-∠1，2∠AED=180°-∠2，
∴∠ADE=90°-12∠1，∠AED=90°-12∠2，
∵在△ADE中，∠A=180°-（∠AED+∠ADE），
∴∠A=12∠1+12∠2，
即2∠A=∠1+∠2．
20. 如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC的平分线，∠A =58°，求∠H的度数．
解：∵∠A=58°,∴∠ABC+∠ACB=180°−∠A=180°−58°=122°…①
∵BH是∠ABC的平分线,∴∠HBC=12∠ABC，
∵∠ACD是△ABC的外角，CH是外角∠ACD的角平分线，
∴∠ACH=12 (∠A+∠ABC)，
∴∠BCH=∠ACB+∠ACH=∠ACB+12 (∠A+∠ABC)，
∵∠H+∠HBC+∠ACB+∠ACH=180°，
∴∠H+12∠ABC+∠ACB+12 (∠A+∠ABC)=180°,
即∠H+(∠ABC+∠ACB)+ 12∠A=180°…②，
把①代入②得,∠H+122°+12×58°=180°，
∴∠H=29°.
21. （1）如图①所示，∠1+∠2与∠B+∠C有什么关系？为什么？
（2）如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时，则∠A与∠α+∠β之间有一种数量关系始终保持不变，请写出这个规律并说明理由．
【答案】（1）∠1+∠2=∠B+∠C;（2）规律：α+β=2∠A．理由见解析
解：（1）∠1+∠2=∠B+∠C，理由如下：
∵如图1，在△AED和△ACB中，
∠1+∠2+∠A=∠A+∠B+∠C=180°（三角形内角和等于180°），
∴∠1+∠2=∠B+∠C（等量代换）；
（2）规律：α+β=2∠A，理由如下：
∵在△ADE中，∠1+∠2=180°﹣∠A（三角形内角和等于180°），
在四边形BCED中，∠BDE+∠DEC+∠B+∠C=360°（四边形内角和等于360°），
又∵根据题（1）得∠1+∠2=∠B+∠C（已证），
∴2（∠1+∠2）+α+β=360°（等量代换），
∴2（180°﹣∠A）+α+β=360°（等量代换），
∴α+β=2∠A．
22. 如图，在△ABC中，BD⊥AC于D．若∠A：∠ABC：∠ACB=3：4：5，E为线段BD上任一点．
（1）试求∠ABD的度数；
（2）求证：∠BEC＞∠A．
解：（1）∵∠A+∠ABC+∠ACB=180°，∠A：∠ABC：∠ACB=3：4：5，
∴∠A=45°，∠B=60°，∠C=75°，
∵BD⊥AC，
∴∠ADB=90°，
∴∠ABD=90°-∠A=45°；
（2）∵∠BEC是△CDE的外角，
∴∠BEC＞∠BDC，
∵∠BDC是△ABD的外角，
∴∠BDC＞∠A，
∴∠BEC＞∠A．
23. 如图，△ABC中，∠A=100∘， = 1 \* GB2 ⑴BI、CI分别平分∠ABC，∠ACB，求∠BIC的度数？ = 2 \* GB2 ⑵若BM、CM分别平分∠ABC，∠ACB的外角平分线，求∠M的度数？
解： = 1 \* GB2 ⑴∵∠A=100°．
∵∠ABC+∠ACB=180°﹣100°=80°．
∵BI、CI分别平分∠ABC，∠ACB，
∴∠IBC=12∠ABC，∠ICB=12∠ACB，
∴∠IBC+∠ICB=12∠ABC+12∠ACB=12（∠ABC+∠ACB）=12×80°=40°，
∴∠I=180°﹣（∠IBC+∠ICB）=180°﹣40°=140°；
= 2 \* GB2 ⑵∵∠ABC+∠ACB=80°，
∴∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB
=360°﹣（∠ABC+∠ACB）=360°﹣80°=280°．
∵BM、CM分别平分∠ABC，∠ACB的外角平分线，
∴∠1=12∠DBC，∠2=12ECB，
∴∠1+∠2=12×280°=140°，
∴∠M=180°﹣∠1﹣∠2=40°．
24. 如图，在△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，且CF∥AD．
（1）如图1，若△ABC是锐角三角形，∠B=30°，∠ACB=70°，则∠CFE= 度；
（2）若图1中的∠B=x，∠ACB=y，则∠CFE= ；（用含x、y的代数式表示）
（3）如图2，若△ABC是钝角三角形，其他条件不变，则（2）中的结论还成立吗？请说明理由．
【答案】（1）20；（2）12y﹣12x；（3）（2）中的结论成立．
解：（1）∵∠B=30°，∠ACB=70°，
∴∠BAC=180°﹣∠B﹣∠ACB=80°，
∵AD平分∠BAC，
∴∠BAD=40°，
∵AE⊥BC，
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°，
∵CF∥AD，
∴∠CFE=∠DAE=20°；
故答案为20；
（2）∵∠BAE=90°﹣∠B，∠BAD=12∠BAC=12（180°﹣∠B﹣∠BCA），
∴∠CFE=∠DAE=∠BAE﹣∠BAD
=90°﹣∠B﹣12（180°﹣∠B﹣∠BCA）
=12（∠BCA﹣∠B）=12y﹣12x．
故答案为12 y﹣12x；
（3）（2）中的结论成立．
∵∠B=x，∠ACB=y，
∴∠BAC=180°﹣x﹣y，
∵AD平分∠BAC，
∴∠DAC=12∠BAC=90°﹣12x﹣12y，
∵CF∥AD，
∴∠ACF=∠DAC=90°﹣12x﹣12y，
∴∠BCF=y+90°﹣12x﹣12y=90°﹣12x+12y，
∴∠ECF=180°﹣∠BCF=90°+12x﹣12y，
∵AE⊥BC，
∴∠FEC=90°，
∴∠CFE=90°﹣∠ECF=12y﹣12x．