数学人教版18.1.1 平行四边形的性质第2课时课后作业题

这是一份数学人教版18.1.1 平行四边形的性质第2课时课后作业题，共6页。
知识点1 平行四边形的对角线互相平分
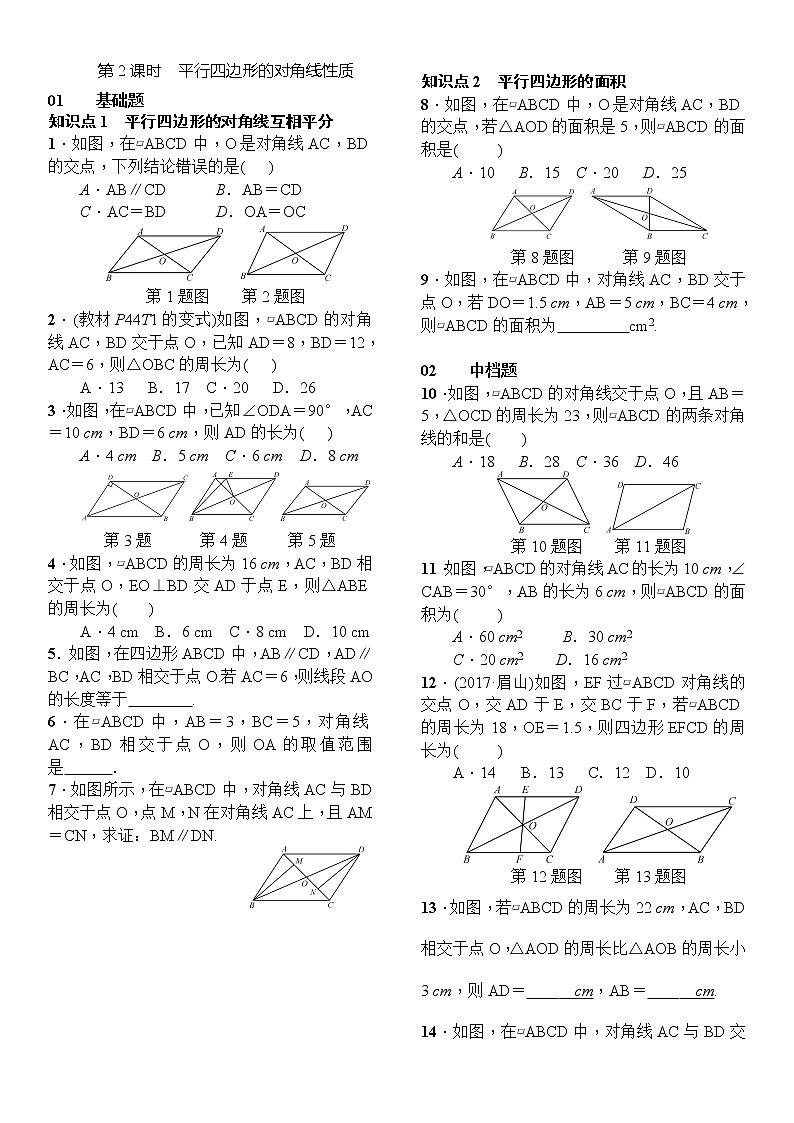
1．如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是( )
A．AB∥CD B．AB＝CD
C．AC＝BD D．OA＝OC

第1题图 第2题图
2．(教材P44T1的变式)如图，▱ABCD的对角线AC，BD交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
A．13 B．17 C．20 D．26
3．如图，在▱ABCD中，已知∠ODA＝90°，AC＝10 cm，BD＝6 cm，则AD的长为( )
A．4 cm B．5 cm C．6 cm D．8 cm
第3题 第4题 第5题
4．如图，▱ABCD的周长为16 cm，AC，BD相交于点O，EO⊥BD交AD于点E，则△ABE的周长为( )
A．4 cm B．6 cm C．8 cm D．10 cm
5．如图，在四边形ABCD中，AB∥CD，AD∥BC，AC，BD相交于点O.若AC＝6，则线段AO的长度等于 .
6．在▱ABCD中，AB＝3，BC＝5，对角线AC，BD相交于点O，则OA的取值范围是 ．
7．如图所示，在▱ABCD中，对角线AC与BD相交于点O，点M，N在对角线AC上，且AM＝CN，求证：BM∥DN.

知识点2 平行四边形的面积
8．如图，在▱ABCD中，O是对角线AC，BD的交点，若△AOD的面积是5，则▱ABCD的面积是( )
A．10 B．15 C．20 D．25

第8题图 第9题图
9．如图，在▱ABCD中，对角线AC，BD交于点O，若DO＝1.5 cm，AB＝5 cm，BC＝4 cm，则▱ABCD的面积为 cm2.
02 中档题
10．如图，▱ABCD的对角线交于点O，且AB＝5，△OCD的周长为23，则▱ABCD的两条对角线的和是( )
A．18 B．28 C．36 D．46

第10题图 第11题图
11．如图，▱ABCD的对角线AC的长为10 cm，∠CAB＝30°，AB的长为6 cm，则▱ABCD的面积为( )
A．60 cm2 B．30 cm2
C．20 cm2 D．16 cm2
12．(2017·眉山)如图，EF过▱ABCD对角线的交点O，交AD于E，交BC于F，若▱ABCD的周长为18，OE＝1.5，则四边形EFCD的周长为( )
A．14 B．13 C．12 D．10

第12题图 第13题图
13．如图，若▱ABCD的周长为22 cm，AC，BD相交于点O，△AOD的周长比△AOB的周长小3 cm，则AD＝ __cm，AB＝ __cm.
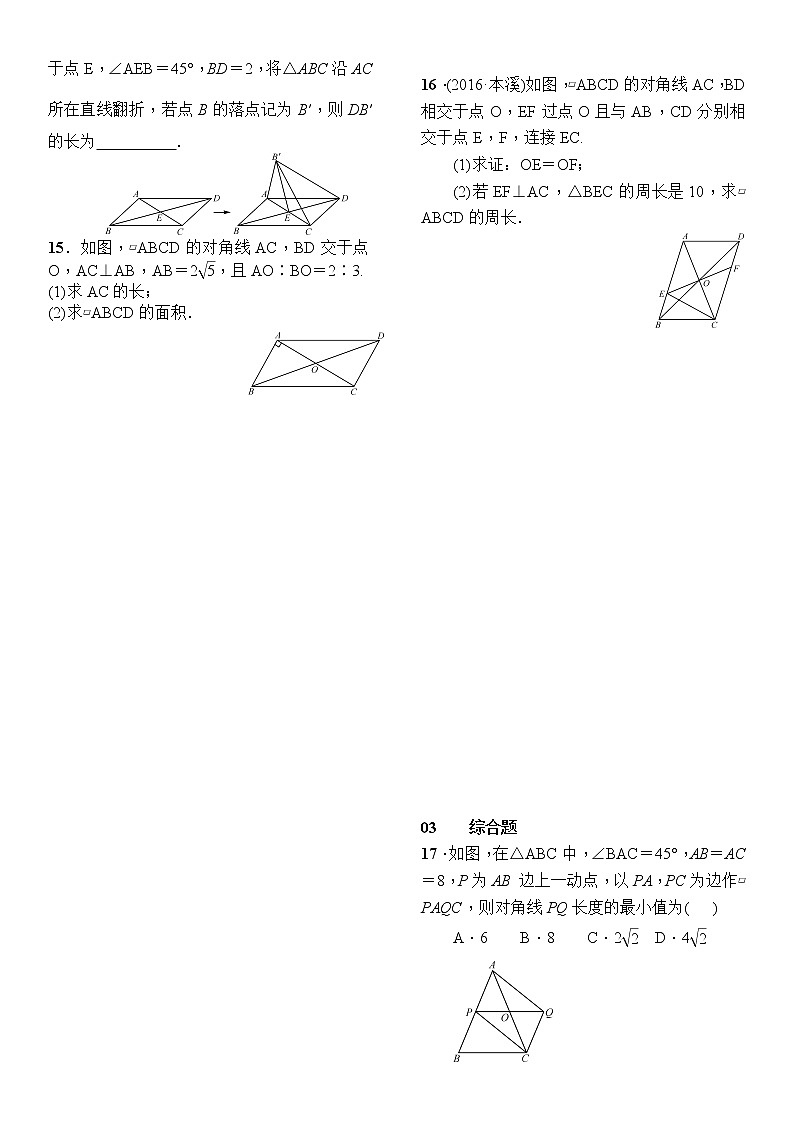
14．如图，在▱ABCD中，对角线AC与BD交于点E，∠AEB＝45°，BD＝2，将△ABC沿AC所在直线翻折，若点B的落点记为B′，则DB′的长为 ．
15．如图，▱ABCD的对角线AC，BD交于点O，AC⊥AB，AB＝2eq \r(5)，且AO∶BO＝2∶3.
(1)求AC的长；
(2)求▱ABCD的面积．
16．(2016·本溪)如图，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AB，CD分别相交于点E，F，连接EC.
(1)求证：OE＝OF；
(2)若EF⊥AC，△BEC的周长是10，求▱ABCD的周长．

03 综合题
17．如图，在△ABC中，∠BAC＝45°，AB＝AC＝8，P为AB 边上一动点，以PA，PC为边作▱PAQC，则对角线PQ长度的最小值为( )
A．6 B．8 C．2eq \r(2) D．4eq \r(2)
第2课时 平行四边形的对角线性质
01 基础题
知识点1 平行四边形的对角线互相平分
1．如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是(C)
A．AB∥CD B．AB＝CD
C．AC＝BD D．OA＝OC

第1题图 第2题图
2．(教材P44T1的变式)如图，▱ABCD的对角线AC，BD交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为(B)
A．13 B．17 C．20 D．26
3．如图，在▱ABCD中，已知∠ODA＝90°，AC＝10 cm，BD＝6 cm，则AD的长为(A)
A．4 cm B．5 cm C．6 cm D．8 cm

第3题图 第4题图
4．如图，▱ABCD的周长为16 cm，AC，BD相交于点O，EO⊥BD交AD于点E，则△ABE的周长为(C)
A．4 cm B．6 cm C．8 cm D．10 cm
5．如图，在四边形ABCD中，AB∥CD，AD∥BC，AC，BD相交于点O.若AC＝6，则线段AO的长度等于3.
6．在▱ABCD中，AB＝3，BC＝5，对角线AC，BD相交于点O，则OA的取值范围是1＜OA＜4．
7．如图所示，在▱ABCD中，对角线AC与BD相交于点O，点M，N在对角线AC上，且AM＝CN，求证：BM∥DN.
证明：∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD.
∵AM＝CN，
∴OM＝ON.
在△BOM和△DON中，
eq \b\lc\{(\a\vs4\al\c1(OB＝OD，,∠BOM＝∠DON，,OM＝ON，))
∴△BOM≌△DON(SAS)．
∴∠OBM＝∠ODN.
∴BM∥DN.
知识点2 平行四边形的面积
8．如图，在▱ABCD中，O是对角线AC，BD的交点，若△AOD的面积是5，则▱ABCD的面积是(C)
A．10 B．15 C．20 D．25

第8题图 第9题图
9．如图，在▱ABCD中，对角线AC，BD交于点O，若DO＝1.5 cm，AB＝5 cm，BC＝4 cm，则▱ABCD的面积为12cm2.
02 中档题
10．如图，▱ABCD的对角线交于点O，且AB＝5，△OCD的周长为23，则▱ABCD的两条对角线的和是(C)
A．18 B．28 C．36 D．46

第10题图 第11题图
11．如图，▱ABCD的对角线AC的长为10 cm，∠CAB＝30°，AB的长为6 cm，则▱ABCD的面积为(B)
A．60 cm2 B．30 cm2
C．20 cm2 D．16 cm2
12．(2017·眉山)如图，EF过▱ABCD对角线的交点O，交AD于E，交BC于F，若▱ABCD的周长为18，OE＝1.5，则四边形EFCD的周长为(C)
A．14 B．13 C．12 D．10

第12题图 第13题图
13．如图，若▱ABCD的周长为22 cm，AC，BD相交于点O，△AOD的周长比△AOB的周长小3 cm，则AD＝4__cm，AB＝7__cm.
14．如图，在▱ABCD中，对角线AC与BD交于点E，∠AEB＝45°，BD＝2，将△ABC沿AC所在直线翻折，若点B的落点记为B′，则DB′的长为eq \r(2)．
15．如图，▱ABCD的对角线AC，BD交于点O，AC⊥AB，AB＝2eq \r(5)，且AO∶BO＝2∶3.
(1)求AC的长；
(2)求▱ABCD的面积．
解：(1)∵AO∶BO＝2∶3，
∴设AO＝2x，BO＝3x
(x＞0)．
∵AC⊥AB，AB＝2eq \r(5)，
∴(2x)2＋(2eq \r(5))2＝(3x)2.
解得x＝2.
∴AO＝4.
∵四边形ABCD是平行四边形，
∴AC＝2AO＝8.
(2)∵S△ABC＝eq \f(1,2)AB·AC
＝eq \f(1,2)×2eq \r(5)×8
＝8eq \r(5)，
∴S▱ABCD＝2S△ABC＝2×8eq \r(5)＝16eq \r(5).
16．(2016·本溪)如图，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AB，CD分别相交于点E，F，连接EC.
(1)求证：OE＝OF；
(2)若EF⊥AC，△BEC的周长是10，求▱ABCD的周长．
解：(1)证明：∵四边形ABCD是平行四边形，
∴OD＝OB，DC∥AB.
∴∠FDO＝∠EBO.
在△DFO和△BEO中，
eq \b\lc\{(\a\vs4\al\c1(∠FDO＝∠EBO，,OD＝OB，,∠FOD＝∠EOB，))
∴△DFO≌△BEO(ASA)．
∴OE＝OF.
(2)∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC，OA＝OC.
∵EF⊥AC，∴AE＝CE.
∵△BEC的周长是10，
∴BC＋BE＋CE＝BC＋BE＋AE＝BC＋AB＝10.
∴C▱ABCD＝2(BC＋AB)＝20.
03 综合题
17．如图，在△ABC中，∠BAC＝45°，AB＝AC＝8，P为AB 边上一动点，以PA，PC为边作▱PAQC，则对角线PQ长度的最小值为(D)
A．6
B．8
C．2eq \r(2)
D．4eq \r(2)