初中数学人教版八年级下册17.2 勾股定理的逆定理优秀ppt课件

这是一份初中数学人教版八年级下册17.2 勾股定理的逆定理优秀ppt课件，共16页。PPT课件主要包含了情境引入，c65，c85，勾股定理的逆定理，动手验证，画图验证，发现结论，归纳总结，特别说明，典例精析等内容，欢迎下载使用。
1.掌握勾股定理的逆定理，并会用它判断一个三角形是不是直角三角形.（重点）2.勾股定理的逆定理的证明.（难点）
1.勾股定理的内容是什么?
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
2.求以线段a、b为直角边的直角三角形的斜边c的长：
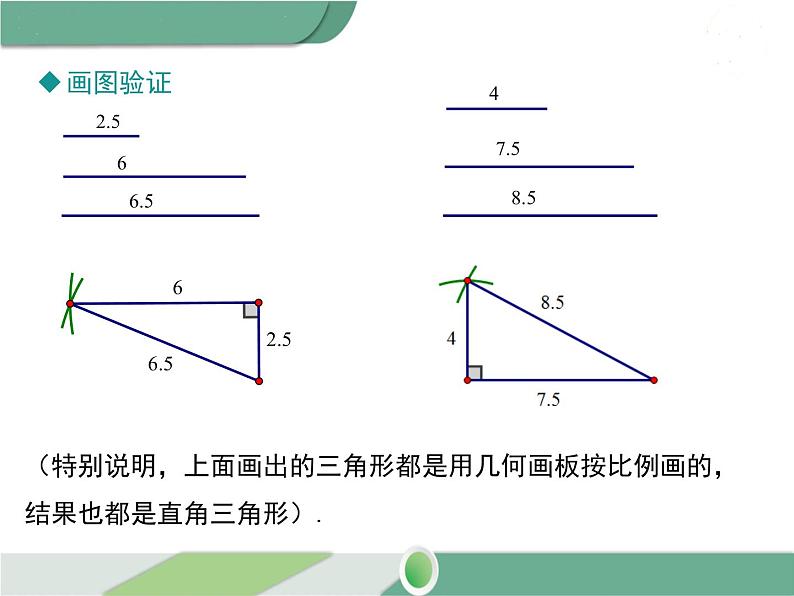
① a＝3，b＝4② a＝2.5，b＝6③ a＝4，b＝7.5
3.分别以上述a、b、c为边的三角形的形状会是什么样的呢？
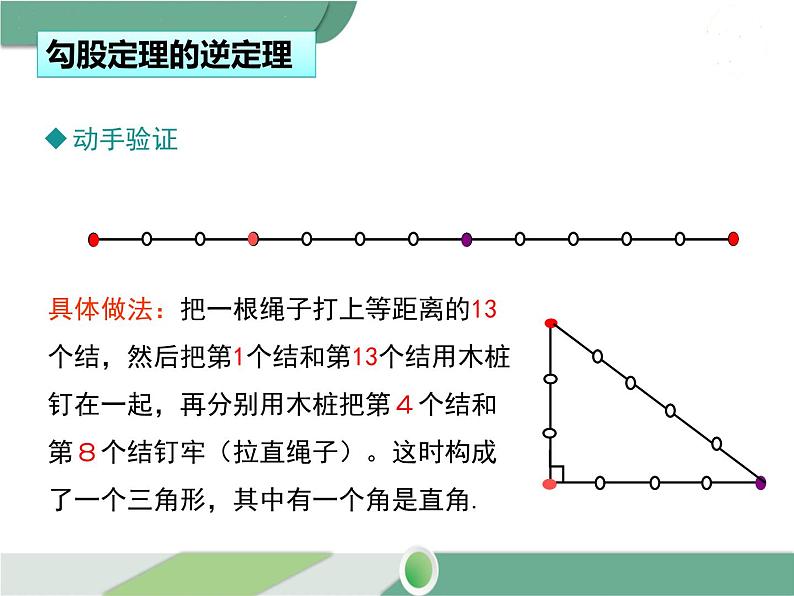
具体做法：把一根绳子打上等距离的13个结，然后把第1个结和第13个结用木桩钉在一起，再分别用木桩把第４个结和第８个结钉牢（拉直绳子）。这时构成了一个三角形，其中有一个角是直角.
（特别说明，上面画出的三角形都是用几何画板按比例画的，结果也都是直角三角形）.
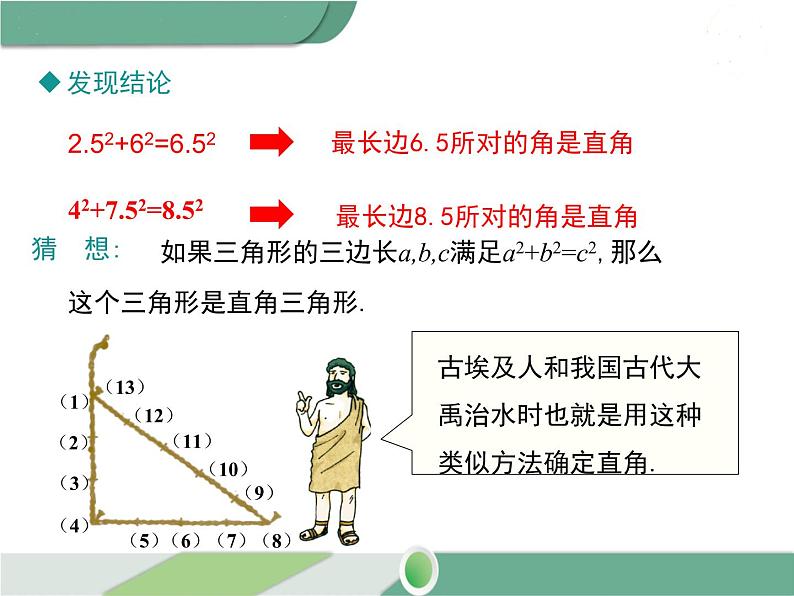
2.52+62=6.52
42+7.52=8.52
最长边6.5所对的角是直角
最长边8.5所对的角是直角
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
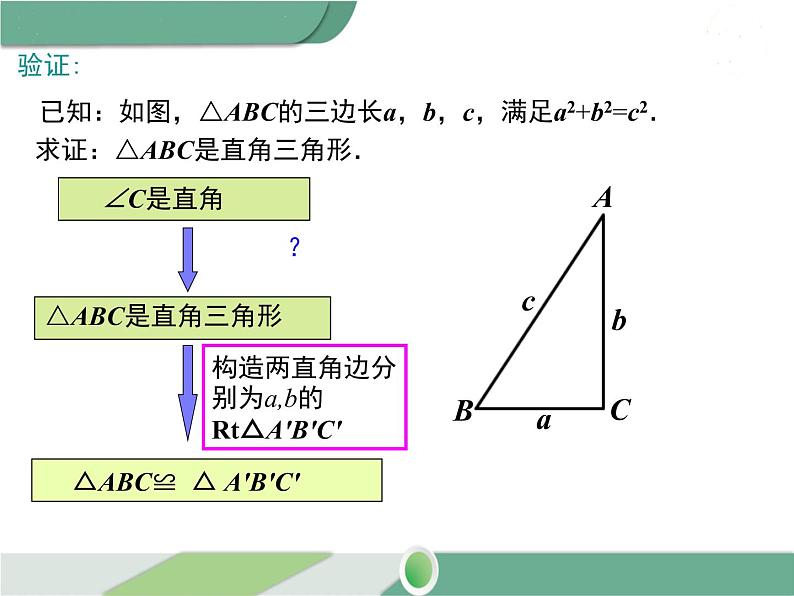
　已知：如图，△ABC的三边长a，b，c，满足a2+b2=c2． 　求证：△ABC是直角三角形．
构造两直角边分别为a,b的Rt△A′B′C′
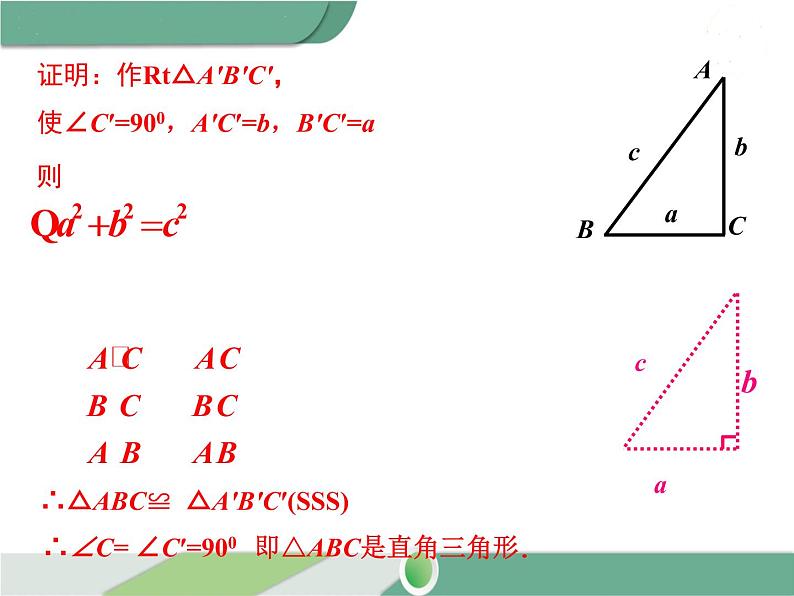
证明：作Rt△A′B′C′，使∠C′=900，A′C′=b，B′C′=a
∴△ABC≌ △A′B′C′(SSS)
∴∠C= ∠C′=900 即△ABC是直角三角形.
如果三角形的三边长a 、b 、c满足 a2+b2=c2那么这个三角形是直角三角形.
勾股定理的逆定理是直角三角形的判定定理，即已知三角形的三边长，且满足两条较小边的平方和等于最长边的平方，即可判断此三角形为直角三角 ，最长边所对角为直角.
例1 下面以a,b,c为边长的三角形是不是直角三角形？如果是,那么哪一个角是直角？
(1) a=25 b=20 c=15;
解：因为152+202=625，252=625，所以152+202=252，根据勾股定理的逆定理，这个三角形是直角三角形，且∠A是直角.
(2) a=13 b=14 c=15;
解：因为132+142=365，152=225，所以132+142≠152，不符合勾股定理的逆定理，所以这个三角形不是直角三角形.
(4) a:b: c=3:4:5;
解：设a=3k,b=4k,c=5k,因为(3k)2+(4k)2=25k2,(5k)2=25k2,所以(3k)2+(4k)2=(5k)2,根据勾股定理的逆定理，这个三角形是直角三角形，∠C是直角.
像15，20，25这样，能成为直角三角形三条边长的正整数，称为勾股数.
奇数类：3，4，5；5，12，13；7，24，25；9，40，41；等等偶数类：4，3，5；6，8，10；8，15，17；10，24，26；等等
一组勾股数，都扩大相同倍数k，得到一组新数，这组数同样是勾股数.
如果三角形的三边长a 、b 、c满足a2+b2=c2那么这个三角形是直角三角形.
是解决直角三角形中的有关计算和证明的主要依据.
是由三边数量关系判定一个三角形是否是直角三角形的依据.
互为逆命题，更是互逆定理.
1.小颖要求△ABC最长边上的高，测得AB=8,AC=6,BC=10,则可知最长边上的高是（ ） A. 5 B. 0.48 C. 4.8 D.48
2.在△ABC中，∠A, ∠B, ∠C的对边分别a,b,c.①若∠C- ∠B= ∠A,则△ABC是直角三角形；②若c2=b2-a2,则△ABC是直角三角形,且∠C=900；③若(c+a)(c-a)=b2,则△ABC是直角三角形;④若∠A：∠B：∠C=5：2：3，则△ABC是直角三角形.以上命题中的假命题个数是（ ）A.1 B.2 C.3 D.4
3. 一根24m的绳子，折成三边长为三个连续偶数的三角形，则三边长分别为 ，此三角形的形状为 .
6m,8cm,10cm
4. 命题：对顶角相等，其逆命题是： .
5.如图，AB=5,AC=3,BC边上的中线AD=2,求△ABC的面积.
解：延长AD并在截取DE=AD,
即△ABC的面积是6.