初中数学19.2.2 一次函数优质课课件ppt

这是一份初中数学19.2.2 一次函数优质课课件ppt，共18页。PPT课件主要包含了学习目标，国家补助金额y，学生数x，有唯一确定的对应值，情景导入，面积S，一边长x，生物电流y，时间x，自主学习等内容，欢迎下载使用。
1.经过练习,观察,认识变量中的自变量与函数.
2.会写出函数关系式,会求函数值.
3.会确定自变量取值范围.
1.国家为了提高农村学生营养水平，每天补助学生营养午餐费3元/人.某中学八（2）班有学生60人，则每天国家需补助 元；该中学共有学生325人，则每天国家补助了 元.设学生数为x（人），国家补助金额为y（元），则y= .
在这个变化过程中，通过计算可以发现： （1） 随 的变化而变化; （2）每当学生数x取定一个值时，国家补助金额y就 .
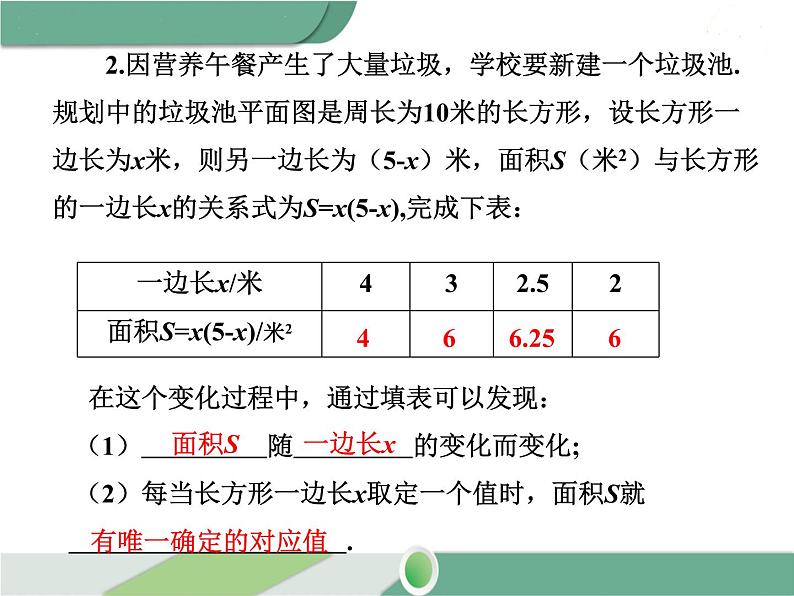
2.因营养午餐产生了大量垃圾，学校要新建一个垃圾池.规划中的垃圾池平面图是周长为10米的长方形，设长方形一边长为x米，则另一边长为（5-x）米，面积S（米2）与长方形的一边长x的关系式为S=x(5-x),完成下表：
在这个变化过程中，通过填表可以发现： （1） 随 的变化而变化; （2）每当长方形一边长x取定一个值时，面积S就 .
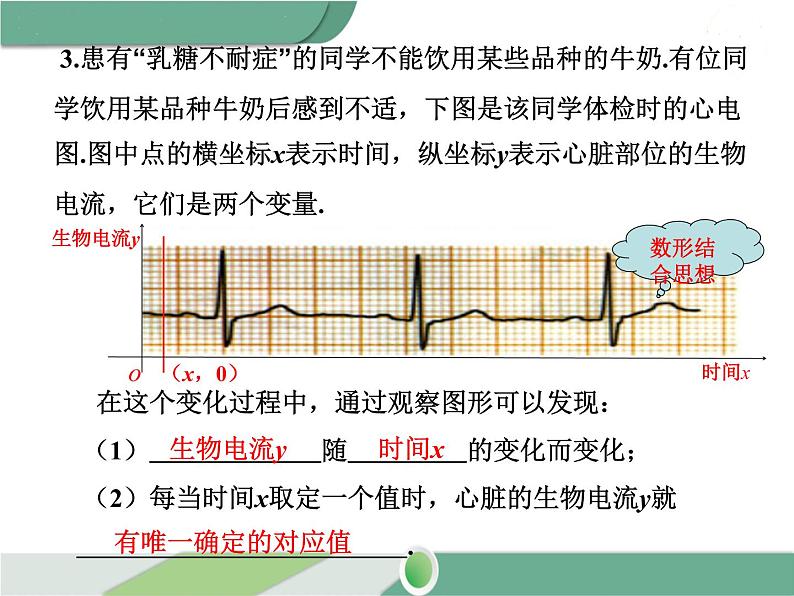
3.患有“乳糖不耐症”的同学不能饮用某些品种的牛奶.有位同学饮用某品种牛奶后感到不适，下图是该同学体检时的心电图.图中点的横坐标x表示时间，纵坐标y表示心脏部位的生物电流，它们是两个变量.
在这个变化过程中，通过观察图形可以发现： （1） 随 的变化而变化； （2）每当时间x取定一个值时，心脏的生物电流y就 .
在上面的每个问题中： 1.每个变化的过程中都存在着（ ）变量； 2.两个变量互相联系，当其中一个变量取定一个值时，另一个变量就( ).
一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每个确定的值，y都有唯一确定的值与其对应，我们就说x是自变量，y是x的函数． 如果当x=a时，y=b，那么b叫做当自变量的值为a时的函数值．
最早给出函数概念明确定义的是詹姆斯·格雷戈里。1667年，他的函数定义为：“它是从一些其它的量经过一系列代数运算而得到的，或者是经过任何其它可以想象的运算而得到的。” 1775年数学家欧拉又给出一个新的函数定义：如果一个变量依赖于另一个变量，使当后一个变量变化时，前一个量也随着变化，那么称第一个量是第二个量的函数。 函数概念从提出到完成，用了二百多年的时间，经历了由不全面到全面，不严密到严密的发展过程，才逐步形成了今天的函数概念。 1859年我国清代数学家李善兰翻译《代数学》一书 时首先用“函数”一词翻译“functin”一词，他解释说： “凡此变数函彼变数，则此为彼之函数”。中国古代用天、 地、人、物表示未知数。李善兰译《代数学》中有“凡式 中含天，为天之函数”这样的语句。 函数思想，是指用函数的概念和性质去分析问题、 转化问题和解决问题。
例如，在“营养午餐”问题中，国家补助金额 y（y=3x）随学生数x的变化而变化，其中学生数x是自变量，补助金额y是x的函数.当x=60时的函数值y=180，当x=325时的函数值y=975.据统计，赣县农村中小学学生数约为70000人，那么国家每天大约需补助 元.
注意： 其中在变化过程中居于主导地位的变量叫做自变量，随之变化的另一个变量叫做自变量的函数（因变量）.
函数与函数值的区别：函数是变量，函数值是确定了自变量时函数所取的某个具体数值，一个函数可能有许多不同的函数值.
例1 下列问题中哪些量是自变量？哪些量是自变量的函数?试写出用自变量表示函数的式子.
（1）改变正方形的边长x，正方形的面积S随之改变.
（2）秀水村的耕地面积是106m2 ,这个村人均占有耕地面积y随这个村人数n的变化而变化.
_______是自变量，_____是______的函数，
关系式是 .
关系式是 .
2.在用解析式表示函数时，要考虑自变量的取值必须使解析式有意义.
用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法，这种式子叫做函数关系式,也称为函数的解析式.
活动：探究函数的关系式及自变量的取值范围
二次根式有意义的条件是：
（1） y＝3x （2） y＝x2＋9  （3） y= （4） y＝
（1）x为任意实数（或全体实数）；
（3）由x-3≠0 得x≠3；
（4）由2x-8≥0得x≥4.
（2） x为任意实数；
例2 求下列函数关系式中自变量x的取值范围： 
巧记自变量的取值范围：分式分母不为零，偶次根下负不行；零次幂底数不为零，整式、奇次根全能行.
例3 为了让学生吃上放心、健康的营养午餐，某贫困县营养办要求食品公司必须用专车定期配送.该公司的一辆配送专车油箱中有汽油50L，如果不再加油，那么油箱中的油量y（单位：L）随行驶里程x（单位：km）的增加而减少，平均耗油量为0.1L/km.
（1）写出表示y与x的函数关系的式子；
（2）指出自变量x的取值范围；
（3）县城至某乡村中学路程为50 km，该汽车从县城往返该县乡村中学配送一次牛奶后油箱中还有多少油？
（4）汽车行驶多少km时，油箱中还有15L油？
解:(1) 函数关系式为: y = 50－0.1x
(2) 由x≥0及50－0.1x ≥0　得　0 ≤ x ≤ 500∴自变量x的取值范围是: 0 ≤ x ≤ 500
(3)当 x = 100时,函数 y 的值为:y=50－0.1×100=40
因此,该汽车配送一次牛奶后油箱中还有40L油.
（4）当函数y=15时，有15= 50－0.1x ，解得自变量x=350， 所以当汽车行驶350km时，油箱中还有15L油.
表示函数关系的式子叫函数解析式
(1)对于一些简单问题的函数解析式，往往可以通过利用已有的公式列出.
例如:底边一定,三角形的面积随高的变化而变化. (a已知).
(2)一些实际问题的函数解析式
先找出自变量x与函数y之间的等量关系
列出关于x, y的二元一次方程
最后还要考虑数量的实际意义
2.本题函数计算问题有两种：第一种已知自变量的值求函数值；第二种反过来已知函数值求自变量的值，实质上是解方程的问题.