初中数学人教版八年级下册17.1 勾股定理第1课时学案设计

第十七章　勾股定理

第1课时　勾股定理及其证明

1.了解勾股定理的文化背景，体验勾股定理的探索过程.

2.了解利用拼图验证勾股定理的方法.

3.能利用勾股定理的数学模型解决现实世界的实际问题.

探索和验证勾股定理.

用拼图的方法证明勾股定理.

一、情景导入，感受新知

创设情境：欣赏图片

国际数学家大会是最高水平的全球性数学学科学术会议，被誉为数学界的“奥运会”，2002年在北京召开了第24届国际数学家大会，上图就是大会会徽的图案.你见过这个图案吗？它由哪些我们学过的基本图形组成？这个图案有什么特别的意义？

这个图案是我国汉代数学家赵爽创造的，被称为“赵爽弦图”.今天我们就用这个图形来验证几何学上的瑰宝：“勾股定理”！

二、自学互研　生成新知

【自主探究】

阅读教材P22～24内容，完成下列问题：

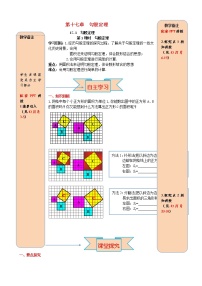
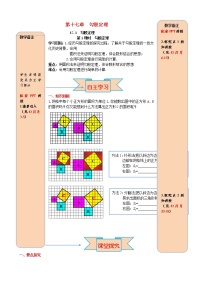
问题1：毕达哥拉斯是古希腊著名的数学家，相传在2500多年前，他在朋友家做客时，发现朋友家用地砖铺成的地面反映了直角三角形的三边的某种数量关系.

(1)现在请你也观察一下，你能有什么发现吗？

(2)你能找出图中正方形A，B，C的面积之间的关系吗？

(3)正方形A，B，C所围等腰直角三角形的三边之间有什么特殊关系？

归纳：等腰直角三角形两条直角边的平方和等于斜边的平方.

【合作探究】

问题2：等腰直角三角形是特殊的直角三角形，一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”呢？

如图，每个小方格的面积均为1，以格点为顶点，①②中分别有一个直角边分别是3，4和2，3的直角三角形.仿照上一活动，我们以这两个直角三角形的三边为边向外作正方形.

(2)想一想，怎样利用小方格计算正方形A，B，C的面积？

(3)正方形A，B，C面积之间的关系是什么？

(2)直角三角形三边之间的关系用命题形式怎样表述？

归纳：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2.

【师生活动】

①明了学情：关注学生能否主动参与探究活动，在讨论中发表自己的见解，倾听他人的意见，对不同的观点进行质疑，从中获益.

②差异指导：对学生存在的疑惑及时引导、点拨.

③生生互助：学生独立观察思考，小组内交流讨论、相互解疑释惑.

三、典例剖析　运用新知

【合作探究】

例1：根据图，利用面积法证明勾股定理.(总统证法)

教师提出问题：上图就是伽菲尔德总统的拼法，你知道他是如何验证的吗？你能用两种方法表示图中的面积吗？

伽菲尔德总统是这样分析的：

S梯形ABCD＝(a＋b)2，

S梯形ABCD＝S△ABE＋S△ECD＋S△AED＝ab＋ab＋c2.

则有(a＋b)2＝ab＋ab＋c2，

化简可得a2＋b2＝c2.

例2：在直角三角形中，各边的长如图①，②，求出未知边的长度.

解：图①中，x＝＝

图②中，x＝＝2

【师生活动】

教师指导学生阅读教材24页，了解赵爽是如何利用拼图的方法来证明命题1的.

学生在弦图验证的基础上，参照教材开展拼图活动，以小组为单位，合作探究.

四、课堂小结　回顾新知

本节课学到了什么知识？同学们还存在什么困惑？

总结：

1.勾股定理的内容.

2.如何验证勾股定理.

3.利用勾股定理，已知直角三角形的两边求第三条边的长.

五、检测反馈　落实新知

1.下面图形中未知正方形的面积为__325__.

2.如图所示，一棵大树在一次强烈台风中于离地面5米处折断倒下，树顶落在离树根12米处.大树在折断之前高为__18__米.

3.求出下列各直角三角形中未知边x的长度.

,①x＝__15__)　,②x＝__12__)　,③x＝__13__)

4.在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，且a＋b＝2，c＝3，求△ABC的面积.

解：∵a＋b＝2，∴a2＋b2＋2ab＝12，又由题知a2＋b2＝c2＝9，∴ab＝，∴S△ABC＝ab＝.

六、课后作业　巩固新知